黑龙江省佳木斯市第八中学、佳木斯市松北高级中学、汤原县高级中学三校2023-2024学年高二下学期期末联考数学试题

这是一份黑龙江省佳木斯市第八中学、佳木斯市松北高级中学、汤原县高级中学三校2023-2024学年高二下学期期末联考数学试题，共8页。试卷主要包含了答卷前，考生务必将自己的姓名等内容，欢迎下载使用。

命题教师：；审题教师：；考试时间：120分钟；试卷总分：150分
注意事项：
1、答卷前，考生务必将自己的姓名、准考证号填写在答题卡上.
2、回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上，写在本试卷上无效.
第I卷（选择题）
一、单项选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中.只有一项是符合题目要求的.
1．设集合，，则A∩B=（ ）
A．B．C．D．
2．命题，的否定是（ ）
A．，B．，
C．，D．，
3．已知随机变量的分布列如下：
则的值为（ ）
A．20B．18C．8D．6
4．不等式的解集为（ ）
A．RB．C．D．
5．已知随机变量服从正态分布，则“”是“”的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
6．2022年10月16日至10月22日，中国共产党第二十次全国人民代表大会在北京召开．会议圆满结束后，某市为了宣传好二十大会议精神，市宣传部决定组织去甲、乙、丙、丁4个村开展二十大宣讲工作，每村至少1人，其中A不去甲村，且不去同一个村，则宣讲的分配方案种数为（ ）
A．158B．162C．180D．198
7．若函数的值域为，则实数的取值范围为（ ）
A． B． C．D．
8．已知，则下列描述正确的是（ ）
A． B．除以5所得的余数是1
C． D．
二、多项选择题：本大题共3小题，每小题6分，共18分.在每小题给出的四个选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.
9．设a，b，c，d为实数，且，则下列不等式正确的有（ ）
A．B．C．D．
10．下列说法正确的是（ ）
A．若随机变量~，则．
B．若随机变量的方差，则．
C．若，，，则事件与事件独立．
D．若随机变量服从正态分布，若，则．
11．2024年元宵节，张同学与陈同学计划去连江人民广场参加猜灯谜活动.张同学家在如图所示的E处，陈同学家在如图所示的F处，人民广场在如图所示的 G 处.下列说法正确的是（ ）
A．张同学到陈同学家的最短路径条数为6条
B．在张同学去人民广场选择的最短路径中，到F处和陈同学汇合并一同前往的概率为
C．张同学在去人民广场途中想先经过花海欣赏灯光秀（花海四周道路均可欣赏），可选的最短路径有22条
D．张同学和陈同学在选择去人民广场的最短路径中，两人相约到人民广场汇合，事件A：张同学经过陈同学家；事件B：从F到人民广场两人的路径没有重叠部分 （路口除外），则.
第II卷（非选择题）
三、填空题：本大题共3小题，每小题5分，共15分.
12．若，且，则的最小值为 .
13．设函数，曲线在点处的切线为.则函数的解析式为 .
14．对于等差数列和等比数列，我国古代很早就有研究成果，北宋大科学家沈括在《梦溪笔谈》中首创的“隙积术”，就是关于高阶等差级数求和的问题．现有一货物堆，从上向下查，第一层有2个货物，第二层比第一层多3个，第三层比第二层多4个，以此类推，记第层货物的个数为，则数列的前10项和 ．
四、解答题：本大题共5小题，共77分.解答应写出文字说明，证明过程或演算步骤.
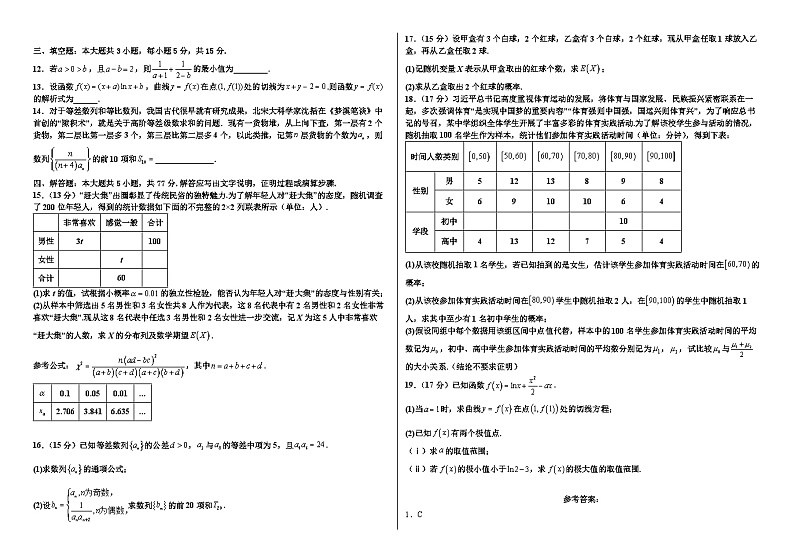
15．（13分）“赶大集”出圈彰显了传统民俗的独特魅力.为了解年轻人对“赶大集”的态度，随机调查了200位年轻人，得到的统计数据如下面的不完整的2×2列联表所示（单位：人）.
(1)求t的值，试根据小概率的独立性检验，能否认为年轻人对“赶大集”的态度与性别有关；
(2)从样本中筛选出5名男性和3名女性共8人作为代表，这8名代表中有2名男性和2名女性非常喜欢“赶大集”.现从这8名代表中任选3名男性和2名女性进一步交流，记X为这5人中非常喜欢“赶大集”的人数，求X的分布列及数学期望.
参考公式：，其中.
16．（15分）已知等差数列的公差，与的等差中项为5，且.
(1)求数列的通项公式；
(2)设求数列的前20项和.
17．（15分）设甲盒有3个白球，2个红球，乙盒有3个白球，2个红球，现从甲盒任取1球放入乙盒，再从乙盒任取2球.
(1)记随机变量X表示从甲盒取出的红球个数，求；
(2)求从乙盒取出2个红球的概率.
18．（17分）习近平总书记高度重视体育运动的发展，将体育与国家发展、民族振兴紧密联系在一起，多次强调体育“是实现中国梦的重要内容”“体育强则中国强，国运兴则体育兴”，为了响应总书记的号召，某中学组织全体学生开展了丰富多彩的体育实践活动.为了解该校学生参与活动的情况，随机抽取100名学生作为样本，统计他们参加体育实践活动时间（单位：分钟），得到下表：
(1)从该校随机抽取1名学生，若已知抽到的是女生，估计该学生参加体育实践活动时间在的概率；
(2)从该校参加体育实践活动时间在学生中随机抽取2人，在的学生中随机抽取1人，求其中至少有1名初中学生的概率；
(3)假设同组中每个数据用该组区间中点值代替，样本中的100名学生参加体育实践活动时间的平均数记为，初中、高中学生参加体育实践活动时间的平均数分别记为，，试比较与的大小关系.（结论不要求证明）
19．（17分）已知函数.
(1)当时，求曲线在点处的切线方程；
(2)已知有两个极值点.
（ⅰ）求的取值范围；
（ⅱ）若的极小值小于，求的极大值的取值范围.
参考答案：
1．C
【详解】由可得，解得或，
所以，
所以，
故选：C.
2．A
【详解】全称存在命题的否定是存在量词命题，并且否定结论，
所以命题，的否定是，.
故选：A
3．B
【详解】根据分布列可知，解得，
，
，
所以.
故选：B.
4．C
【详解】由，得，
得，解得，
所以不等式的解集为，
故选：C
5．A
【详解】随机变量服从正态分布，，，
当时，，
而当时，，
所以“”是“”的充分不必要条件.
故选：A
6．B
【详解】当A单独去某一个村时，从乙、丙、丁3个村中选择1个安排，有种情况，
剩下的4个人安排到3个村，有种情况，
故有种情况，
当A和中的某一个一起去某个村时，
先从选择1个，再从乙、丙、丁3个村中选择1个安排，有种情况，
再安排另外3个人，每个人去1个村，有种情况，
故有种情况，
综上，共有种情况.
故选：B
7．C
【详解】①时，，值域为，满足题意；
②时，若的值域为，
则，解得，
综上，.
故选：C.
8．B
【详解】，
令，可得，再令，可得，
,故A错误．
由于，即展开式各项系数和系数和，
故，，故C错误．
由题意，，
显然，除了最后一项外，其余各项均能被5整除，除以5所得的余数是1，故B正确．
因为，
所以，
所以，故D错误．
故选：B．
9．AD
【详解】对于A，由和不等式性质可得，故A正确；
对于B，因，若取，，，，
则，，所以，故B错误；
对于C，因，若取，，，，
则，，所以，故C错误；
对于D，因为，则，又因则，
由不等式的同向皆正可乘性得，，故，故D正确．
故选：AD．
10．ACD
【详解】随机变量，则，故A正确；
随机变量的方差，则，故B错误；
由，即事件与事件独立，故C正确；
随机变量服从正态分布，，
则，故D正确．
故选：ACD．
11．AB
【详解】对于A：最短路径为共走4格，其中向上走2格，向右走2格，条数为，A正确；
对于B：在张同学去人民广场选择的最短路径中，
总的基本事件：共走7格，其中向上走3格，向右走4格，即有种走法，
到F处和陈同学汇合并一同前往，首先到处，有种走法，再到人民广场，共走3格，其中向上走1格，向右走2格，即有种走法，则到F处和陈同学汇合并一同前往的基本事件有种，
则概率为，B正确；
对于C：在张同学去人民广场选择的最短路径共种走法，若途中不经过花海欣赏灯光秀，
①先从走到有种走法，再从走到有2种走法，则途中不经过花海欣赏灯光秀有种走法，
②先从走到有种走法，再从走到有种走法，则途中不经过花海欣赏灯光秀有种走法，
③先从走到，再走到有种走法，
综合得途中不经过花海欣赏灯光秀总共有种走法，
则欣赏灯光秀有种走法，C错误；
对于D：，D错误.
故选：AB.
【点睛】方法点睛：网格中的最短路径问题，可以转化为格中，有格向上，向右的问题来解答.
12．/0.8
【详解】，，，
，
，
，当且仅当时，即时取等号．
故答案为：．
13．
【详解】，
因为曲线在点处的切线为，
所以，即，解得，
所以.
故答案为：.
14．
【详解】由题意可知，，，，……，，
所以，
，
，
所以数列，
.
故答案为：
15．(1)，能；
(2)分布列见解析，.
【详解】（1）由题意可知：，解得，
2×2列联表如下：
.
根据小概率值的独立性检验，认为年轻人对“赶大集”的态度与性别有关，
此推断犯错误的概率不大于0.01.
（2）设进一步交流的男性中非常喜欢“赶大集”的人数为m，女性中非常喜欢“赶大集”的人数为n，
则，且X的所有可能取值为1，2，3，4.
，
，
，
.
所以X的分布列为
所以.
16．(1)数列的通项公式为；
(2)数列的前20项和为.
【详解】（1）因为为等差数列，且与的等差中项为5，
所以，解得，
因为，
所以，解得，
因为，所以，
所以，
故数列的通项公式为；
（2）由题知，
即
所以
，
故数列的前20项和为.
17．(1)
(2)
【详解】（1）由题可知，随机变量可能的取值有.
所以
分布列如下：
所以.
（2）(i)若，则此时甲盒取出来了1个白球放入乙盒，
此时乙盒有4个白球，2个红球，所以从乙盒取出2个红球的概率为
(ii) 若，则此时甲盒取出来了1个红球放入乙盒，
此时乙盒有3个白球，3个红球，所以从乙盒取出2个红球的概率为；
所以从乙盒取出2个红球的概率为.
18．(1)
(2)
(3)
【详解】（1）女生共有人，
记事件A为“从所有调查学生中随机抽取1人，女生被抽到”，
事件B为“从所有调查学生中随机抽取1人，参加体育活动时间在”，
由题意可知，，
因此，
所以从该校随机抽取1名学生，若已知抽到的是女生，
估计该学生参加体育活动时间在的概率为.
（2）时间在的学生有人，
活动时间在的初中学生有人，
记事件C为“从参加体育活动时间在的学生中随机抽取2人，抽到初中学生”，
事件D为“从参加体育活动时间在的学生中随机抽取1人，抽到的是初中学生”，
由题意知，事件C，D相互独立，
且,
所以至少有1名初中学生的概率；
（3）根据男女生人数先补全初中学生各区间人数：
初中生的总运动时间，
高中生的总运动时间，
又，，，
可得由.
19．(1)
(2)（ⅰ）；（ⅱ）
解；（ⅱ）设有两个不同的正实数根，根据单调性可知的极值点，结合零点代换可得，构建，结合单调性分析可得，则，即可得取值范围.
【详解】（1）当时，则，，
可得，，
即切点坐标为，切线斜率，
所以曲线在处的切线方程为，即.
（2）（ⅰ）由题意可知：的定义域为，，
令，可得，
原题意等价于有两个不同的正实数根，
因为，当且仅当，即时，等号成立，
可知，所以的取值范围；
（ii）由（i）可知：有两个不同的正实数根，，
不妨设，可知，
当时，；当或时，；
可知在，上单调递增，在上单调递减，
所以为的极小值点，为的极大值点，
对于的极值点，则，
可得，
设，则，
当时，；当时，；
可知在内单调递增，在上单调递减，
则，可知，则，
又因为在区间上单调递增，则，
所以的极大值的取值范围是.
2
3
6
非常喜欢
感觉一般
合计
男性
3t
100
女性
t
合计
60
0.1
0.05
0.01
…
2.706
3.841
6.635
…
时间人数类别
性别
男
5
12
13
8
9
8
女
6
9
10
10
6
4
学段
初中
10
高中
4
13
12
7
5
4
非常喜欢
感觉一般
合计
男性
60
40
100
女性
80
20
100
合计
140
60
200
X
1
2
3
4
P
0
1
时间人数类别
性别
男
5
12
13
8
9
8
女
6
9
10
10
6
4
学段
初中
7
8
11
11
10
8
高中
4
13
12
7
5
4