北师大版九年级上册1 菱形的性质与判定课前预习课件ppt

这是一份北师大版九年级上册1 菱形的性质与判定课前预习课件ppt，共31页。

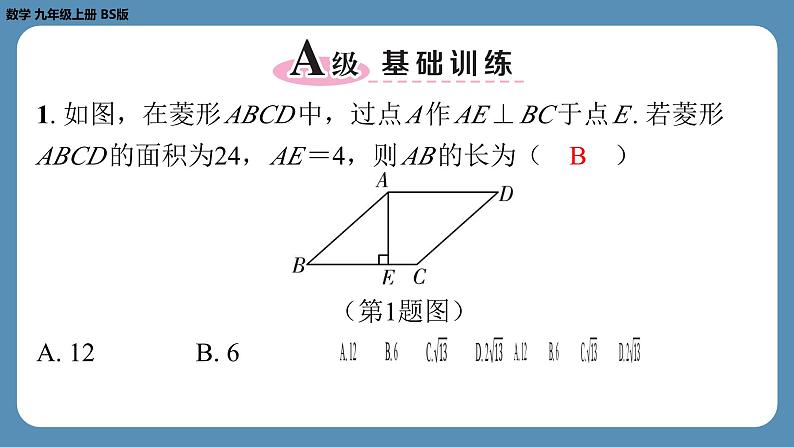
1. 如图，在菱形 ABCD 中，过点 A 作 AE ⊥ BC 于点 E . 若菱形 ABCD 的面积为24， AE ＝4，则 AB 的长为（　B　）
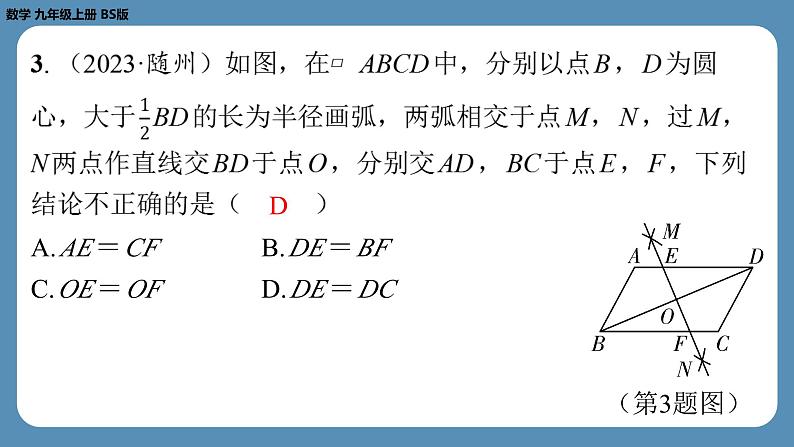
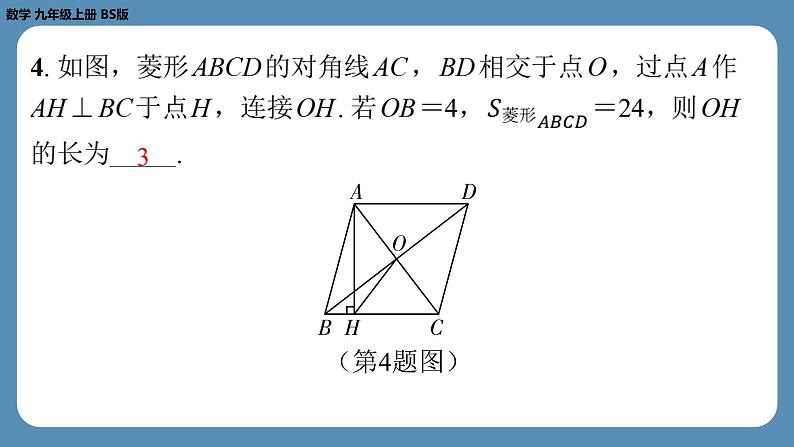
2. （2022·河南）如图，在菱形 ABCD 中，对角线 AC ， BD 相交 于点 O ，点 E 为 CD 的中点.若 OE ＝3，则菱形 ABCD 的周长为 （　C　）
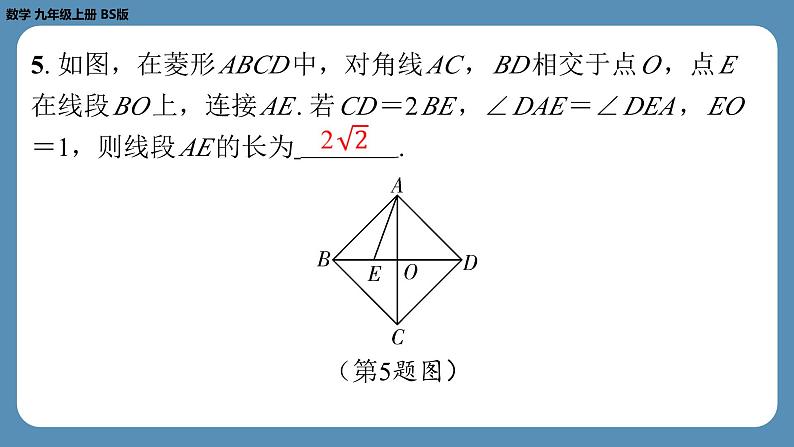
5. 如图，在菱形 ABCD 中，对角线 AC ， BD 相交于点 O ，点 E 在线段 BO 上，连接 AE . 若 CD ＝2 BE ，∠ DAE ＝∠ DEA ， EO ＝1，则线段 AE 的长为 ⁠.
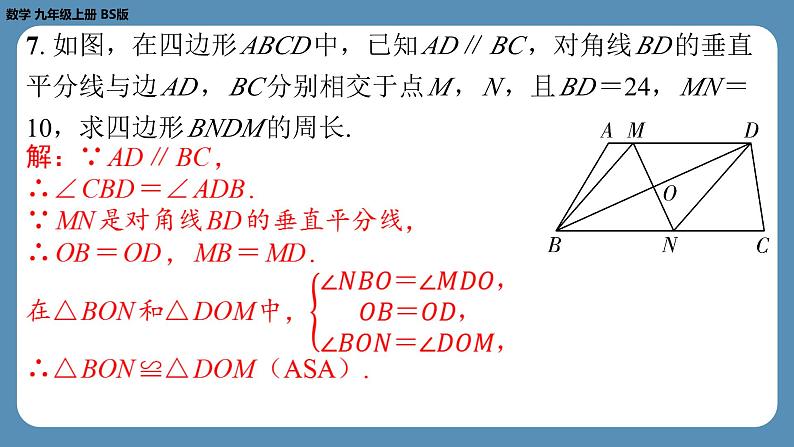
7. 如图，在四边形 ABCD 中，已知 AD ∥ BC ，对角线 BD 的垂直 平分线与边 AD ， BC 分别相交于点 M ， N ，且 BD ＝24， MN ＝ 10，求四边形 BNDM 的周长.
8. 如图，在四边形 ABCD 中，已知 AB ＝ AD ， BD 平分∠ ABC ， AC ⊥ BD ，垂足为 O .
（1）求证：四边形 ABCD 是菱形；
∴△ AOD ≌△ COB （ASA）.∴ AD ＝ BC . 又∵ AD ∥ BC ，∴四边形 ABCD 是平行四边形.又∵ AC ⊥ BD ，∴▱ ABCD 是菱形.
9. 如图， AC 是菱形 ABCD 的对角线，点 P 是 AC 上的一个动 点，过点 P 分别作 AB 和 BC 的垂线，垂足分别是 F ， E . 若菱形 的周长是12，面积是6，则 PE ＋ PF 的值是 ⁠.
10. 在平面直角坐标系中，点 A ， B ， C ， D 的坐标分别为（－ 3，0），（ x ， y ），（0，4），（－6， z ）.若以点 A ， B ， C ， D 为顶点的四边形是菱形，则 z 的值为 ⁠.
11. 如图，在等腰三角形 ABC 中， AB ＝ AC ， AD 平分∠ BAC 交 BC 于点 D . 在线段 AD 上任取一点 P （点 A 除外），过点 P 作 EF ∥ AB ，分别交 AC ， BC 于点 E ， F ，作 PQ ∥ AC ，交 AB 于点 Q ，连接 QE .
（1）判断四边形 AQPE 的形状，并说明理由；
（1）解：四边形 AQPE 为菱形.理由如下：∵ EF ∥ AB ， PQ ∥ AC ，∴四边形 AQPE 为平行四边形，∠ BAD ＝∠ EPA . ∵ AD 平分∠ BAC ，∴∠ CAD ＝∠ BAD . ∴∠ CAD ＝∠ EPA . ∴ EA ＝ EP . ∴▱ AQPE 为菱形.
（2）当点 P 在何处时，四边形 AQPE 的面积为四边形 EQBF 面 积的一半？
∵四边形 AQPE 为菱形，
∴ AD ⊥ EQ .
∵ AB ＝ AC ， AD 平分∠ BAC ，
∴ AD ⊥ BC . ∴ EQ ∥ BC .
又∵ EF ∥ AB ，
∴四边形 EQBF 为平行四边形.
如图，过点 E 作 EN ⊥ AB 于点 N .
∴ S菱形 AQPE ＝ EP · EN
12. 如图，已知菱形 ABCD 的对角线 BD ＝8，另一条对角线的长 为6，点 M ， N 分别是边 BC ， CD 的中点，点 P 是对角线 BD 上 一点.求 PM ＋ PN 的最小值.
解：如答图，作点 M 关于 BD 的对称点 Q ，连接 NQ ，交 BD 于 点 P ，连接 NP .
易知 PQ ＝ PM ，∴ PM ＋ PN ＝ PQ ＋ PN .
由“两点之间，线段最短”可知，此时 PM ＋ PN 的值最小.连接 AC ，则点 P 是 AC 的中点.
∵四边形 ABCD 是菱形，
∴ AC ⊥ BD ，∠ QBP ＝∠ MBP . ∴点 Q 在 AB 上.
由折叠的性质，得 MQ ⊥ BD ，∴ AC ∥ MQ .
∵点 M 为 BC 的中点，∴点 Q 为 AB 的中点.
∵点 N 为 CD 的中点，四边形 ABCD 是菱形，
∴ BQ ∥ CN ， BQ ＝ CN .
∴四边形 QBCN 是平行四边形.
∴ PQ ∥ AD .
又∵点 Q 是 AB 的中点，
∴ PQ 是△ ABD 的中位线，
即点 P 是 BD 的中点.
同理可得， PM 是△ ABC 的中位线，
∴点 P 是 AC 的中点.
∴点 P 是菱形 ABCD 对角线的交点.
在Rt△ BPC 中，由勾股定理，得
∴ PM ＋ PN ＝ PQ ＋ PN ＝ QN ＝5.
故 PM ＋ PN 的最小值为5.
13. （选做）已知 AC 是菱形 ABCD 的对角线，点 E 在 BC 上，连 接 AE ，且 AE ＝ AC .
（1）如图1，若∠ D ＝30°， BE ＝4，求 AC 的长；
（1）解：∵四边形 ABCD 是菱形，∠ D ＝30°，
如图1，过点 E 作 EF ⊥ AB 于点 F ，则∠ BEF ＝90°－∠ B ＝90°－30°＝60°.
∵ AE ＝ AC ，
∴∠ AEC ＝∠ ACE ＝75°.
∴∠ AEF ＝180°－∠ AEC －∠ BEF ＝180°－75°－60°＝45°.
∴△ AEF 是等腰直角三角形.
（2）如图2，过点 C 作 CH ⊥ AB 于点 H ，点 F 为 CD 上一点，连 接 AF ，∠ DAF ＝∠ BAE ， DF ＝ AH ，求证： AB ＝3 AH .
（2）证明：如图2，在线段 AB 上取一点 G ，使 BG ＝ BE ，连接 CG .
∴∠ B ＝∠ D ， AB ＝ AD ＝ BC .
∴△ BAE ≌△ DAF （ASA）.
∴ BE ＝ DF ， AE ＝ AF . ∴ BG ＝ DF .
∴△ CBG ≌△ ABE （SAS）.∴ CG ＝ AE .
又∵ AE ＝ AC ，∴ CG ＝ AC .
∵ CH ⊥ AB ，∴ AH ＝ HG .
∵ AH ＝ DF ， BG ＝ DF ，
∴ AH ＝ HG ＝ BG .
∴ AB ＝3 AH .