





还剩17页未读,
继续阅读
北师版高中数学必修第一册2.2对函数的进一步认识2.2.2(一)函数的表示法(一)(课件)
展开
这是一份北师版高中数学必修第一册2.2对函数的进一步认识2.2.2(一)函数的表示法(一)(课件),共25页。
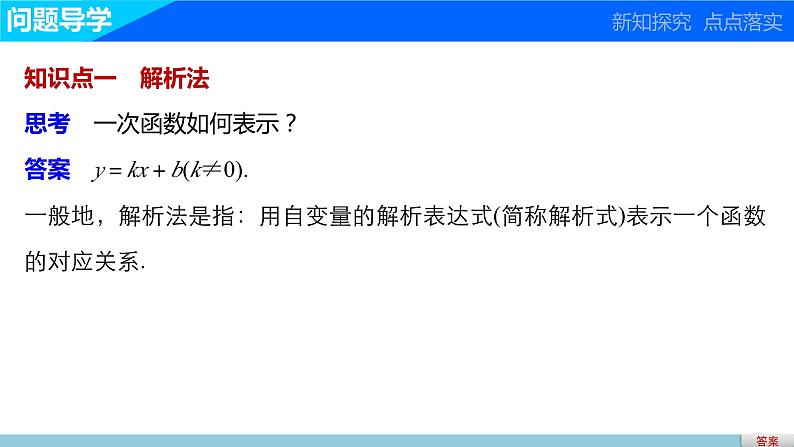
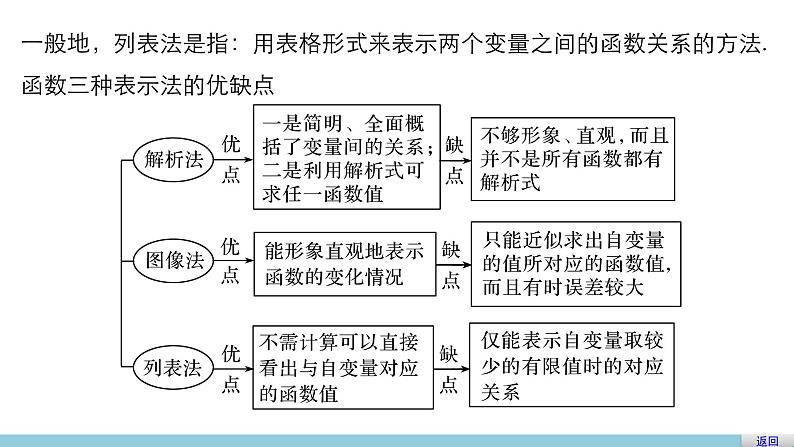
第二章 §2 对函数的进一步认识2.2 函数的表示法(一)1.了解函数的三种表示法及各自的优缺点;2.掌握求函数解析式的常见方法;3.尝试作图和从图像上获取有用的信息.问题导学题型探究达标检测学习目标知识点一 解析法思考 一次函数如何表示?答案 y=kx+b(k≠0).一般地,解析法是指:用自变量的解析表达式(简称解析式)表示一个函数的对应关系.答案问题导学 新知探究 点点落实答案知识点二 图像法思考 要知道林黛玉长什么样,你觉得一个字的描述和一张二寸照片哪个更直观?答案 一图胜千言.一般地,图像法是指:用 表示两个变量之间的对应关系;这样可以直观形象地表示两变量间的变化趋势.图像答案知识点三 列表法思考 在街头随机找100人,请他们依次随意地写一个数字.设找的人序号为x,x=1,2,3,…,100.第x个人写下的数字为y,则x与y之间是不是函数关系?能否用解析式表示?答案 对于任一个x的值,都有一个他写的数字与之对应,故x,y之间是函数关系,但因为人是随机找的,数字是随意写的,故难以用解析式表示.这时可以制作一个表格来表示x的值与y的值之间的对应关系.返回一般地,列表法是指:用表格形式来表示两个变量之间的函数关系的方法.函数三种表示法的优缺点解析答案题型探究 重点难点 个个击破类型一 解析式的求法例1 根据下列条件,求f(x)的解析式.(1)f[f(x)]=2x-1,其中f(x)为一次函数;解 由题意,设f(x)=ax+b(a≠0),∵f(f(x))=af(x)+b=a[ax+b]+b=a2x+ab+b=2x-1,解析答案反思与感悟(2)若f(x+1)=x2+2x;解 方法一 设x+1=t,则x=t-1.∴f(x+1)=f(t)=(t-1)2+2(t-1)=(t-1)(t-1+2)=t2-1.∴f(x)=x2-1.方法二 f(x+1)=(x+1)2-1,∴f(x)=x2-1.(3)f(x)+2f(-x)=x2+2x.解 ∵f(x)+2f(-x)=x2+2x,将x换成-x,得f(-x)+2f(x)=x2-2x,∴联立以上两式消去f(-x),得3f(x)=x2-6x,1.如果已知函数类型,可以用待定系数法.2.如果已知f(g(x))的表达式,想求f(x)的解析式,可以设t=g(x),然后把f(g(x))中每一个x都换成t.3.如果条件是一个关于f(x)、f(-x)的方程,我们可以用x的任意性进行赋值.如把每一个x换成-x,其目的是再得到一个关于f(x)、f(-x)的方程,然后消元消去f(-x).解析答案跟踪训练1 根据下列条件,求f(x)的解析式.(1)f(x)是一次函数,且满足3f(x+1)-f(x)=2x+9;解 由题意,设函数为f(x)=ax+b(a≠0),∵3f(x+1)-f(x)=2x+9,∴3a(x+1)+3b-ax-b=2x+9,即2ax+3a+2b=2x+9,∴a=1,b=3.∴所求函数解析式为f(x)=x+3.解析答案(2)f(x+1)=x2+4x+1;解 设x+1=t,则x=t-1,f(t)=(t-1)2+4(t-1)+1,即f(t)=t2+2t-2.∴所求函数解析式为f(x)=x2+2x-2.解析答案类型二 图像的画法及应用解 由1-x2≥0解得函数定义域为[-1,1].当x=±1时,y有最小值0.当x=0时,y有最大值1.反思与感悟 画图时一般很难把所有点都描出来,故为了使画出来的图能反映变量间的变化规律,我们要尽量选择关键点:最高点、最低点和与x,y轴的交点.反思与感悟解析答案跟踪训练2 一水池有2个进水口,1个出水口,进出水速度如图甲、乙所示.某天0点到6点,该水池的蓄水量如图丙所示.(至少打开一个水口)给出以下3个论断:①0点到3点只进水不出水;②3点到4点不进水只出水;③4点到6点不进水不出水.则正确论断的个数是( )A.0 B.1 C.2 D.3解析 由题意可知在0点到3点这段时间,每小时进水量为2,即2个进水口同时进水且不出水,所以①正确;从丙图可知3点到4点水量减少了1,所以应该是有一个进水口进水,同时出水口也出水,故②错;当两个进水口同时进水,出水口也同时出水时,水量保持不变,也可由题干中的“至少打开一个水口”知③错.故选B.答案 B解析答案类型三 函数表示法的选择例3 下表是某校高一(1)班三名同学在高一学年度六次数学测试的成绩及班级平均分表.(1)选择合适的方法表示测试序号与成绩的关系;解 不能用解析法表示,用图像法表示为宜.在同一个坐标系内画出这四个函数的图像如下:解析答案(2)根据表示出来的函数关系对这三位同学的学习情况进行分析.解 王伟同学的数学成绩始终高于班级平均水平,学习情况比较稳定而且成绩优秀.张城同学的数学成绩不稳定,总是在班级平均水平上下波动,而且波动幅度较大.赵磊同学的数学成绩低于班级平均水平,但他的成绩曲线呈上升趋势,表明他的数学成绩在稳步提高.反思与感悟 函数的三种表示方法都有各自的优点,有些函数能用三种方法表示,有些只能用其中的一种来表示.反思与感悟跟踪训练3 画出y=2x2-4x-3,x∈(0,3]的图像,并求出y的最大值,最小值.解 y=2x2-4x-3(0
第二章 §2 对函数的进一步认识2.2 函数的表示法(一)1.了解函数的三种表示法及各自的优缺点;2.掌握求函数解析式的常见方法;3.尝试作图和从图像上获取有用的信息.问题导学题型探究达标检测学习目标知识点一 解析法思考 一次函数如何表示?答案 y=kx+b(k≠0).一般地,解析法是指:用自变量的解析表达式(简称解析式)表示一个函数的对应关系.答案问题导学 新知探究 点点落实答案知识点二 图像法思考 要知道林黛玉长什么样,你觉得一个字的描述和一张二寸照片哪个更直观?答案 一图胜千言.一般地,图像法是指:用 表示两个变量之间的对应关系;这样可以直观形象地表示两变量间的变化趋势.图像答案知识点三 列表法思考 在街头随机找100人,请他们依次随意地写一个数字.设找的人序号为x,x=1,2,3,…,100.第x个人写下的数字为y,则x与y之间是不是函数关系?能否用解析式表示?答案 对于任一个x的值,都有一个他写的数字与之对应,故x,y之间是函数关系,但因为人是随机找的,数字是随意写的,故难以用解析式表示.这时可以制作一个表格来表示x的值与y的值之间的对应关系.返回一般地,列表法是指:用表格形式来表示两个变量之间的函数关系的方法.函数三种表示法的优缺点解析答案题型探究 重点难点 个个击破类型一 解析式的求法例1 根据下列条件,求f(x)的解析式.(1)f[f(x)]=2x-1,其中f(x)为一次函数;解 由题意,设f(x)=ax+b(a≠0),∵f(f(x))=af(x)+b=a[ax+b]+b=a2x+ab+b=2x-1,解析答案反思与感悟(2)若f(x+1)=x2+2x;解 方法一 设x+1=t,则x=t-1.∴f(x+1)=f(t)=(t-1)2+2(t-1)=(t-1)(t-1+2)=t2-1.∴f(x)=x2-1.方法二 f(x+1)=(x+1)2-1,∴f(x)=x2-1.(3)f(x)+2f(-x)=x2+2x.解 ∵f(x)+2f(-x)=x2+2x,将x换成-x,得f(-x)+2f(x)=x2-2x,∴联立以上两式消去f(-x),得3f(x)=x2-6x,1.如果已知函数类型,可以用待定系数法.2.如果已知f(g(x))的表达式,想求f(x)的解析式,可以设t=g(x),然后把f(g(x))中每一个x都换成t.3.如果条件是一个关于f(x)、f(-x)的方程,我们可以用x的任意性进行赋值.如把每一个x换成-x,其目的是再得到一个关于f(x)、f(-x)的方程,然后消元消去f(-x).解析答案跟踪训练1 根据下列条件,求f(x)的解析式.(1)f(x)是一次函数,且满足3f(x+1)-f(x)=2x+9;解 由题意,设函数为f(x)=ax+b(a≠0),∵3f(x+1)-f(x)=2x+9,∴3a(x+1)+3b-ax-b=2x+9,即2ax+3a+2b=2x+9,∴a=1,b=3.∴所求函数解析式为f(x)=x+3.解析答案(2)f(x+1)=x2+4x+1;解 设x+1=t,则x=t-1,f(t)=(t-1)2+4(t-1)+1,即f(t)=t2+2t-2.∴所求函数解析式为f(x)=x2+2x-2.解析答案类型二 图像的画法及应用解 由1-x2≥0解得函数定义域为[-1,1].当x=±1时,y有最小值0.当x=0时,y有最大值1.反思与感悟 画图时一般很难把所有点都描出来,故为了使画出来的图能反映变量间的变化规律,我们要尽量选择关键点:最高点、最低点和与x,y轴的交点.反思与感悟解析答案跟踪训练2 一水池有2个进水口,1个出水口,进出水速度如图甲、乙所示.某天0点到6点,该水池的蓄水量如图丙所示.(至少打开一个水口)给出以下3个论断:①0点到3点只进水不出水;②3点到4点不进水只出水;③4点到6点不进水不出水.则正确论断的个数是( )A.0 B.1 C.2 D.3解析 由题意可知在0点到3点这段时间,每小时进水量为2,即2个进水口同时进水且不出水,所以①正确;从丙图可知3点到4点水量减少了1,所以应该是有一个进水口进水,同时出水口也出水,故②错;当两个进水口同时进水,出水口也同时出水时,水量保持不变,也可由题干中的“至少打开一个水口”知③错.故选B.答案 B解析答案类型三 函数表示法的选择例3 下表是某校高一(1)班三名同学在高一学年度六次数学测试的成绩及班级平均分表.(1)选择合适的方法表示测试序号与成绩的关系;解 不能用解析法表示,用图像法表示为宜.在同一个坐标系内画出这四个函数的图像如下:解析答案(2)根据表示出来的函数关系对这三位同学的学习情况进行分析.解 王伟同学的数学成绩始终高于班级平均水平,学习情况比较稳定而且成绩优秀.张城同学的数学成绩不稳定,总是在班级平均水平上下波动,而且波动幅度较大.赵磊同学的数学成绩低于班级平均水平,但他的成绩曲线呈上升趋势,表明他的数学成绩在稳步提高.反思与感悟 函数的三种表示方法都有各自的优点,有些函数能用三种方法表示,有些只能用其中的一种来表示.反思与感悟跟踪训练3 画出y=2x2-4x-3,x∈(0,3]的图像,并求出y的最大值,最小值.解 y=2x2-4x-3(0
相关资料
更多









