高中数学北师大版必修14二次函数性质的再研究课文ppt课件

这是一份高中数学北师大版必修14二次函数性质的再研究课文ppt课件，共30页。PPT课件主要包含了学习目标，达标检测等内容，欢迎下载使用。

1.能熟练地对一般的二次函数的解析式进行配方，理解在二次函数的图像中a，b，c(或a，h，k)的作用；2.研究二次函数图像移动的方法，并能迁移到其他函数；3.掌握二次函数的三种不同表示形式，能正确地运用题设条件求出解析式，并能将函数解析式和图像进行正确转换；4.掌握二次函数的性质：定义域、值域、单调性及最值；5.掌握二次函数在闭区间上的最值的求法，初步学会求含有参数的二次函数的值域和最值.
知识点一　二次函数的配方法思考　y＝4x2－4x－1如何配方？你能由此求出方程4x2－4x－1＝0的根吗？
问题导学 　　　　新知探究 点点落实
令y＝0，即4x2－4x－1＝0，
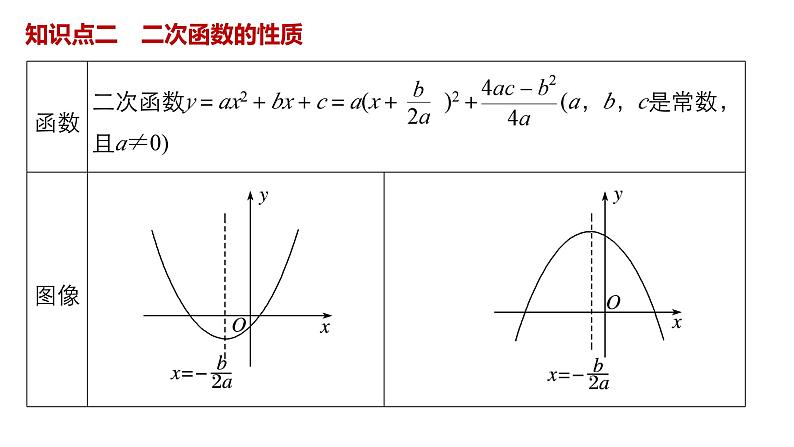
知识点二　二次函数的性质
知识点三　图像变换思考　y＝x2和y＝2(x＋1)2＋3的图像之间有什么关系？答案　y＝x2的图像各点纵坐标变为原来的2倍，可得y＝2x2的图像；再把y＝2x2的图像向左平移1个单位，再上移3个单位，得y＝2(x＋1)2＋3的图像.
题型探究 　　　　重点难点 个个击破
类型一　二次函数的图像例1　如图是二次函数y＝ax2＋bx＋c图像的一部分，图像过点A(－3,0)，对称轴为x＝－1.给出下面四个结论：①b2>4ac；②2a－b＝1；③a－b＋c＝0；④5a解析　因为图像开口向下且顶点纵坐标大于0，所以b2－4ac>0，①正确；
结合图像，当x＝－1时，y>0，即a－b＋c>0，③错误；由对称轴为x＝－1知，b＝2a，因为5>2，a<0，所以5a<2a，即5a处理二次函数y＝ax2＋bx＋c(a≠0)的图像问题，主要是考虑其图像特征如开口、顶点、与x轴、y轴交点、对称轴等与系数a，b，c之间的关系.
跟踪训练1　二次函数f(x)＝x2＋bx＋c的图像向左平移2个单位长度，再向上平移3个单位长度，得到二次函数f(x)＝x2－2x＋1的图像，则b＝______，c＝______.解析　f(x)＝x2－2x＋1＝(x－1)2，其图像顶点为(1,0).将二次函数f(x)＝x2－2x＋1的图像向下平移3个单位长度，再向右平移2个单位长度后的图像的顶点为(3，－3)，得到的抛物线为y＝(x－3)2－3，即f(x)＝x2＋bx＋c，∴(x－3)2－3＝x2＋bx＋c，即x2－6x＋6＝x2＋bx＋c，∴b＝－6，c＝6.
类型二　二次函数解析式的求解例2　已知二次函数y＝ax2＋bx＋c(a≠0)的图像与x轴相交于点A(－3,0)，对称轴为x＝－1，顶点M到x轴的距离为2，求此函数的解析式.
解　方法一　因为二次函数图像的对称轴是x＝－1，又顶点M到x轴的距离为2，所以顶点的坐标为(－1,2)或(－1，－2)，故可得二次函数的解析式为y＝a(x＋1)2＋2或y＝a(x＋1)2－2.因为图像过点A(－3,0)，所以0＝a(－3＋1)2＋2或0＝a(－3＋1)2－2，
方法二　因为二次函数图像的对称轴为x＝－1，又图像过点A(－3,0)，所以点A关于对称轴的对称点A′(1,0)也在图像上，所以可得二次函数的解析式为y＝a(x＋3)(x－1).由题意得顶点坐标为(－1,2)或(－1，－2)，
求二次函数解析式的常见设法(1)一般式，设为y＝ax2＋bx＋c(a≠0)；(2)顶点式，若已知二次函数图像的顶点为(h，k)，则函数的解析式可以设为y＝a(x－h)2＋k(a≠0)；(3)两根式，若已知二次函数y＝ax2＋bx＋c(a≠0)对应的方程ax2＋bx＋c＝0(a≠0)有两个根x1，x2，则函数的解析式可以设为y＝a(x－x1)(x－x2)(a≠0).利用已知条件寻找对应的设法，往往可使函数解析式的求解变得简单.
跟踪训练2　已知f(x)是关于x的二次函数，且满足f(0)＝1，f(x＋1)＝f(x)＋2x，求f(x)的解析式.解　设二次函数的解析式为f(x)＝ax2＋bx＋c(a≠0)，
故二次函数的解析式为f(x)＝x2－x＋1.
类型三　二次函数的最值或值域
(1)求函数图像的顶点坐标、对称轴方程和最值；
(2)若x∈[1,4]，求函数值域.解　由于3∈[1,4]，所以函数在区间[1,3]上是减函数，
跟踪训练3　已知函数f(x)＝ax2＋2ax＋1在区间[－1,2]上有最大值4，求实数a的值.解　f(x)＝a(x＋1)2＋1－a.(1)当a＝0时，函数f(x)在区间[－1,2]上的值不变，恒为常数1，不符合题意，舍去.(2)当a>0时，函数f(x)在区间[－1,2]上是增函数，
(3)当a<0时，函数f(x)在区间[－1,2]上是减函数，最大值为f(－1)＝1－a＝4，解得a＝－3.
1.二次函数f(x)＝ax2＋bx＋c(a≠0)与g(x)＝bx2＋ax＋c(b≠0)的图像可能是下图中的(　　)
即f(x)，g(x)的图像的对称轴位于y轴的同一侧，由此排除A，B；由C，D中给出的图像，可判定f(x)，g(x)的图像的开口方向相反，
即f(x)，g(x)的图像的对称轴都位于y轴右侧，排除C，选D.答案　D
2.设二次函数y＝f(x)满足f(4＋x)＝f(4－x)，又f(x)在[4，＋∞)上是减函数，且f(a)≥f(0)，则实数a的取值范围是(　　)A.a≥4 B.0≤a≤8C.a<0 D.a<0或a≥8解析　由题意知二次函数f(x)的图像关于直线x＝4对称，则有f(0)＝f(8).因为f(x)在[4，＋∞)上是减函数，所以在(－∞，4]上是增函数.当a∈(－∞，4]时，由f(a)≥f(0)，得0≤a≤4；当a∈[4，＋∞)时，由f(a)≥f(0)，即f(a)≥f(8)，得4≤a≤8.综上可知0≤a≤8.
3.已知f(x)＝x2＋bx＋c，且f(－1)＝f(3)，则(　　)A.f(1)>c>f(－1) B.f(1)f(－1)>f(1) D.c4.已知二次函数f(x)＝x2－6x＋8，x∈[2，a]且f(x)的最小值为f(a)，则a的取值范围是_____.解析　二次函数f(x)的图像的对称轴为x＝3，要使f(x)＝x2－6x＋8在区间[2，a]上的最小值为f(a)，只需函数f(x)在区间[2，a]上是减函数，所以25.已知二次函数y＝ x2＋2x＋1.(1)写出函数图像的开口方向、顶点坐标、对称轴、最值，并指出它可由y＝x2的图像怎样变化得到；
∴函数图像的开口向上，顶点坐标是(－2，－1)，对称轴是直线x＝－2.
(2)求函数图像与y轴、x轴的交点；解　令x＝0，则y＝1，
∴函数图像与y轴交于(0,1).
(3)作出函数的图像；解　函数图像如图.
(4)求函数的单调区间；解　由图像可知，函数的单调递减区间是(－∞，－2]，单调递增区间是[－2，＋∞).(5)观察图像：当x为何值时，y>0？当x为何值时，y＝0？当x为何值时，y<0?
1.配方法是重要的数学方法，在处理二次函数图像变换，研究二次函数性质时使用频繁.2.二次函数图像变换规律可以推广到一般函数，即：