北师版高中数学必修第一册3.3指数函数(一)（课件）

这是一份北师版高中数学必修第一册3.3指数函数(一)（课件），共23页。
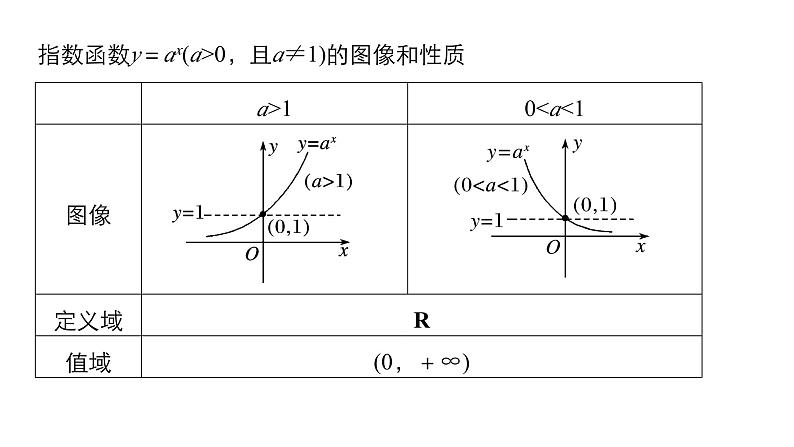
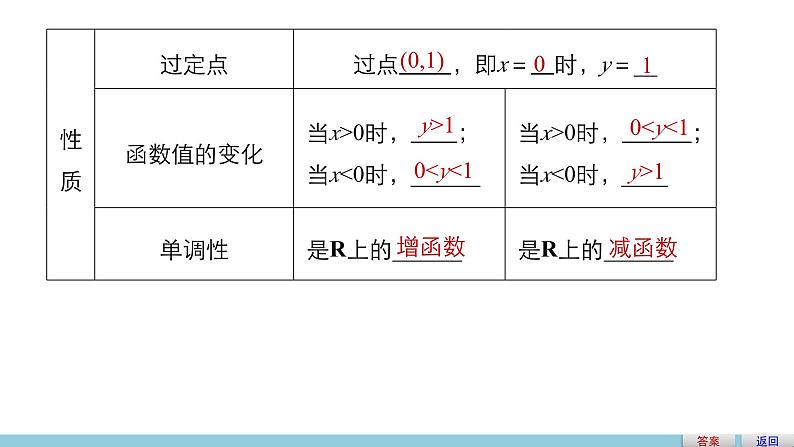
第三章　指数函数和对数函数§3　指数函数(一)1.理解指数函数的概念，了解对底数的限制条件的合理性；2.掌握指数函数图像的性质；3.会应用指数函数的性质求复合函数的定义域、值域.问题导学题型探究达标检测学习目标知识点一　指数函数思考1　y＝2x与y＝x2有什么不同？答案　y＝2x.它的底为常数，自变量出现在指数的位置上，而y＝x2恰好反过来.一般地， 叫作指数函数，其中x是自变量，函数的定义域是 .答案问题导学 　　　　新知探究 点点落实函数y＝ax(a>0，且a≠1)R答案思考2　指数函数定义中为什么规定了a>0且a≠1?答案　原因如下：在实数范围内函数值不存在；(3)如果a＝1，y＝1x＝1，是个常数函数，没有研究的必要.答案知识点二　指数函数的图像和性质思考　函数的性质包括哪些？如何探索指数函数的性质？答案　函数性质通常包括定义域、值域、特殊点、单调性、最值、奇偶性.可以通过描点作图，先研究具体的指数函数性质，再推广至一般.指数函数y＝ax(a>0，且a≠1)的图像和性质y>101)的图像.解　函数y＝a|x|是偶函数，当x≥0时，y＝ax.由已知a>1，根据指数图像可得y＝a|x|如图.解析答案类型三　求指数函数与其他函数复合所得函数的定义域、值域例3　求下列函数的定义域、值域.解　函数的定义域为R(∵对一切x∈R,3x≠－1).又∵3x>0,1＋3x>1，∴值域为(0,1).解析答案(2)y＝4x－2x＋1.反思与感悟指数函数y＝ax与y＝f(x)的复合方式主要是y＝af(x)和y＝f(ax).函数y＝af(x)(a>0且a≠1)与函数f(x)的定义域相同，求与指数函数有关的函数的值域时，要达到指数函数本身的要求，并利用好指数函数的单调性.解析答案跟踪训练3　求下列函数的定义域、值域：(1)解　由x－1≠0得x≠1，所以函数定义域为{x|x≠1}.所以函数值域为{y|y>0且y≠1}.(2)所以函数值域为{y|y≥1}.解析答案返回123达标检测41.下列各函数中，是指数函数的是(　　)A.y＝(－3)xB.y＝－3xC.y＝3x－15D答案2.若函数y＝(2a－1)x(x是自变量)是指数函数，则a的取值范围是(　　)A.a>0，且a≠1 B.a≥0，且a≠112345答案C3.函数f(x)＝ax＋1(a>0，a≠1)必过定点(　　)A.(0,1) B.(0,2)C.(1,1) D.(－1,1)12345D答案4.已知3x＝10，则这样的x(　　)A.存在且只有一个B.存在且不只一个C.存在且x0且a≠1)这一结构形式，即ax的系数是1，指数是x且系数为1.2.指数函数y＝ax(a>0且a≠1)的性质分底数a>1,00且a≠1)与函数f(x)的定义域相同.4.求函数y＝af(x)(a>0且a≠1)的值域的方法如下：(1)换元，令t＝f(x)，并求出函数t＝f(x)的定义域；(2)求t＝f(x)的值域t∈M；(3)利用y＝at的单调性求y＝at在t∈M上的值域.本课结束