2025年高考数学一轮复习（基础版）课时精讲第3章　§3.2　导数与函数的单调性（2份打包，原卷版+含解析）

这是一份2025年高考数学一轮复习（基础版）课时精讲第3章　§3.2　导数与函数的单调性（2份打包，原卷版+含解析），文件包含2025年高考数学一轮复习基础版课时精讲第3章§32导数与函数的单调性原卷版doc、2025年高考数学一轮复习基础版课时精讲第3章§32导数与函数的单调性含解析doc等2份试卷配套教学资源，其中试卷共16页， 欢迎下载使用。

1.结合实例，借助几何直观了解函数的单调性与导数的关系.
2.能利用导数研究函数的单调性，会求函数的单调区间(其中多项式函数一般不超过三次).
3.会利用函数的单调性判断大小，求参数的取值范围等简单应用．
知识梳理
1．函数的单调性与导数的关系
2.利用导数判断函数单调性的步骤
第1步，确定函数f(x)的定义域；
第2步，求出导数f′(x)的零点；
第3步，用f′(x)的零点将f(x)的定义域划分为若干个区间，列表给出f′(x)在各区间上的正负，由此得出函数y＝f(x)在定义域内的单调性．
常用结论
1．若函数f(x)在(a，b)上单调递增，则当x∈(a，b)时，f′(x)≥0恒成立；若函数f(x)在(a，b)上单调递减，则当x∈(a，b)时，f′(x)≤0恒成立．
2．若函数f(x)在(a，b)上存在单调递增区间，则当x∈(a，b)时，f′(x)>0有解；若函数f(x)在(a，b)上存在单调递减区间，则当x∈(a，b)时，f′(x)<0有解．
自主诊断
1．判断下列结论是否正确．(请在括号中打“√”或“×”)
(1)如果函数f(x)在某个区间内恒有f′(x)＝0，则f(x)在此区间内没有单调性．( )
(2)在(a，b)内f′(x)≤0且f′(x)＝0的根有有限个，则f(x)在(a，b)内单调递减．( )
(3)若函数f(x)在定义域上都有f′(x)>0，则f(x)在定义域上一定单调递增．( )
(4)函数f(x)＝x－sin x在R上是增函数．( )
2.(多选)如图是函数y＝f(x)的导函数y＝f′(x)的图象，则下列判断正确的是( )
A．在区间(－2,1)上f(x)单调递增
B．在区间(2,3)上f(x)单调递减
C．在区间(4,5)上f(x)单调递增
D．在区间(3,5)上f(x)单调递减
3．已知f(x)＝x3＋x2－x的单调递增区间为________．
4．已知f(x)＝2x2－ax＋ln x在区间(1，＋∞)上单调递增，则实数a的取值范围是________．
题型一 不含参函数的单调性
例1 (1)函数f(x)＝xln x－3x＋2的单调递减区间为________．
(2)若函数f(x)＝eq \f(ln x＋1,ex)，则函数f(x)的单调递增区间为________．
跟踪训练1 已知函数f(x)＝xsin x＋cs x，x∈[0,2π]，则f(x)的单调递减区间为( )
A.eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(π,2))) B.eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)，\f(3π,2))) C．(π，2π) D.eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,2)，2π))
题型二 含参数的函数的单调性
例2 已知函数g(x)＝(x－a－1)ex－(x－a)2，讨论函数g(x)的单调性．
跟踪训练2 已知函数f(x)＝eq \f(2x－a,x＋12).
(1)当a＝0时，求曲线y＝f(x)在点(0，f(0))处的切线方程；
(2)求函数f(x)的单调区间．
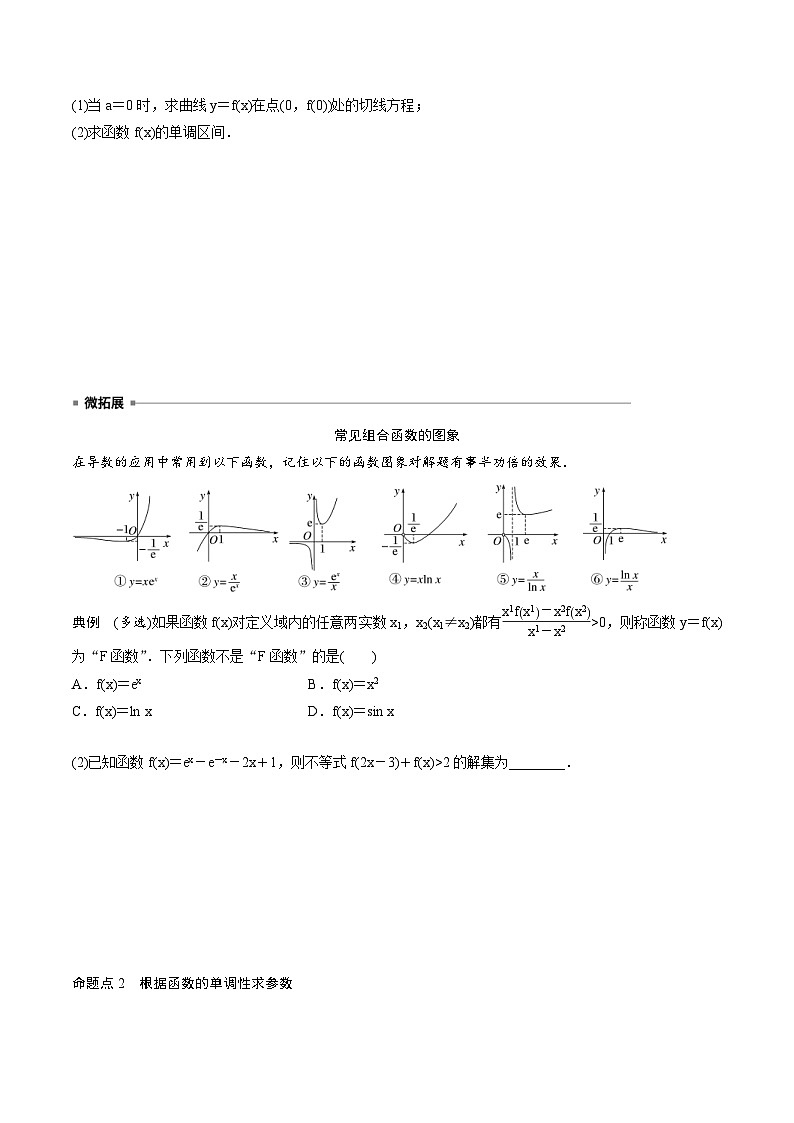
常见组合函数的图象
在导数的应用中常用到以下函数，记住以下的函数图象对解题有事半功倍的效果．

典例 (多选)如果函数f(x)对定义域内的任意两实数x1，x2(x1≠x2)都有eq \f(x1fx1－x2fx2,x1－x2)>0，则称函数y＝f(x)为“F函数”．下列函数不是“F函数”的是( )
A．f(x)＝ex B．f(x)＝x2
C．f(x)＝ln x D．f(x)＝sin x
(2)已知函数f(x)＝ex－e－x－2x＋1，则不等式f(2x－3)＋f(x)>2的解集为________．
命题点2 根据函数的单调性求参数
例4 已知函数f(x)＝ln x－eq \f(1,2)ax2－2x(a≠0)．
(1)若f(x)在[1,4]上单调递减，求实数a的取值范围；
(2)若f(x)在[1,4]上存在单调递减区间，求实数a的取值范围．
跟踪训练3
(1)函数f(x)的图象如图所示，设f(x)的导函数为f′(x)，则f(x)·f′(x)>0的解集为( )
A．(1,6) B．(1,4)
C．(－∞，1)∪(6，＋∞) D．(1,4)∪(6，＋∞)
(2)已知函数f(x)＝(1－x)ln x＋ax在(1，＋∞)上不单调，则a的取值范围是( )
A．(0，＋∞) B．(1，＋∞)
C．[0，＋∞) D．[1，＋∞)
课时精练
一、单项选择题
1．函数f(x)＝(x－3)ex的单调递减区间是( )
A．(－∞，2) B．(0,3) C．(1,4) D．(2，＋∞)
2．已知f′(x)是函数y＝f(x)的导函数，且y＝f′(x)的图象如图所示， 则函数y＝f(x)的图象可能是( )
3．已知函数f(x)＝eq \f(1,3)ax3＋x2＋x＋4，则“a≥0”是“f(x)在R上单调递增”的( )
A．充要条件 B．充分不必要条件
C．必要不充分条件 D．既不充分也不必要条件
4．已知函数f(x)＝aex－ln x在区间(1,2)上单调递增，则a的最小值为( )
A．e2 B．e C．e－1 D．e－2
5．已知f(x)是定义在R上的偶函数，当x≥0时，f(x)＝ex＋sin x，则不等式f(2x－1)A.eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1＋π,2)，＋∞)) B.eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(1＋π,2)))
C.eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(1＋eπ,2))) D.eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1－π,2)，\f(1＋π,2)))
二、多项选择题
6．若函数f(x)＝eq \f(1,2)x2－9ln x在区间[m－1，m＋1]上单调，则实数m的值可以是( )
A．1 B．2 C．3 D．4
7．已知函数f(x)＝eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(1,x)))ln x，且a＝f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(2,3)))，b＝f eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(4,5)))，c＝ SKIPIF 1 < 0 ，则( )
A．a>b B．b>a C．c>b D．c>a
三、填空题
8．函数f(x)＝e－xcs x(x∈(0，π))的单调递增区间为________．
9．若函数f(x)＝x3＋bx2＋x恰有三个单调区间，则实数b的取值范围为________．
10．已知定义在(－3,3)上的奇函数y＝f(x)的导函数是f′(x)，当x≥0时，y＝f(x)的图象如图所示，则关于x的不等式eq \f(f′x,x)>0的解集为________．
11．已知函数f(x)＝eq \f(3x,a)－2x2＋ln x(a>0)，若函数f(x)在[1,2]上不单调，则实数a的取值范围是________．
四、解答题
12．已知函数f(x)＝(a－x)ln x.
(1)求曲线y＝f(x)在点(1，f(1))处的切线方程；
(2)若函数f(x)在(0，＋∞)上单调递减，求实数a的取值范围．
条件
恒有
结论
函数y＝f(x)在区间(a，b)上可导
f′(x)>0
f(x)在区间(a，b)上单调递增
f′(x)<0
f(x)在区间(a，b)上单调递减
f′(x)＝0
f(x)在区间(a，b)上是常数函数