河南省驻马店市正阳县2023-2024学年八年级上学期期末素质测试数学试卷(含答案)

这是一份河南省驻马店市正阳县2023-2024学年八年级上学期期末素质测试数学试卷(含答案)，共9页。试卷主要包含了本试卷分第I卷 和第Ⅱ卷 ，下列运算正确的是等内容，欢迎下载使用。

(考试时间: 100分钟试卷满分: 120分)
注意事项：
1.本试卷分第I卷(选择题) 和第Ⅱ卷(非选择题) .答题前，考生务必将自己的姓名、准考证号填写在答题卡上.
2.回答第I卷时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其它答案标号.写在本试卷上无效.
3.回答第Ⅱ卷时，将答案写在答题卡上。写在本试卷上无效.
第I卷
一、选择题(本大题共10个小题，每小题3分，共30分，下列各小题均有四个答案，其中只有一个是正确的)
1. 1971年，被考古界誉为红山文化象征的“中华第一龙”——红山碧玉龙在赤峰市翁牛特旗赛沁塔拉嘎查出土，赤峰也因此被誉为“中华玉龙之乡”.红山碧玉龙的发现，不仅让中国人找到了龙的头，也充分印证了中国龙文化的远流长.除此之外，还有许多关于龙的图案，下列标志图案中属于轴对称图形的是( )
2. 下列长度的各组线段能构成三角形的是( )
A. 4,2,2 B. 3,2,6 C. 3,5,8 D.3,4,5
3. 人字梯中间一般会设计一“拉杆”，这样做的道理是( )
A. 两点之间，线段最短 B. 垂线段最短
C. 两直线平行，内错角相等 D. 三角形具有稳定性
4.下列运算正确的是( )
A.3a+2a=5a2 B.a³⋅a⁴=a¹²
C.-2x2y3=-8x6y3 D.a+b²=a²+b²
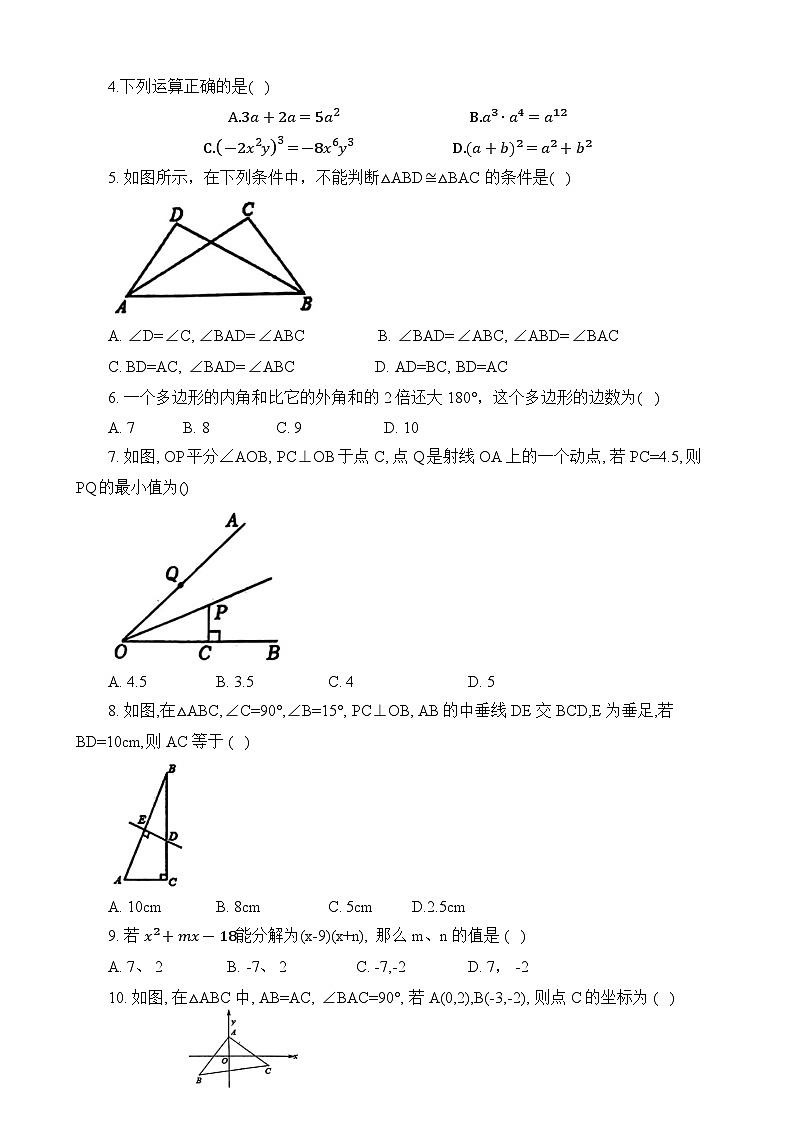
5. 如图所示，在下列条件中，不能判断△ABD≅△BAC的条件是( )
A. ∠D=∠C, ∠BAD=∠ABC B. ∠BAD=∠ABC, ∠ABD=∠BAC
C. BD=AC, ∠BAD=∠ABC D. AD=BC, BD=AC
6. 一个多边形的内角和比它的外角和的2倍还大180°，这个多边形的边数为( )
A. 7 B. 8 C. 9 D. 10
7. 如图, OP平分∠AOB, PC⊥OB于点C, 点Q是射线OA上的一个动点, 若PC=4.5, 则PQ的最小值为()
A. 4.5 B. 3.5 C. 4 D. 5
8. 如图,在△ABC,∠C=90°,∠B=15°, PC⊥OB, AB的中垂线DE交BCD,E为垂足,若BD=10cm,则AC等于 ( )
A. 10cm B. 8cm C. 5cm
9. 若 x²+mx-18能分解为(x-9)(x+n), 那么m、n的值是 ( )
A. 7、 2 B. -7、 2C. -7,-2 D. 7， -2
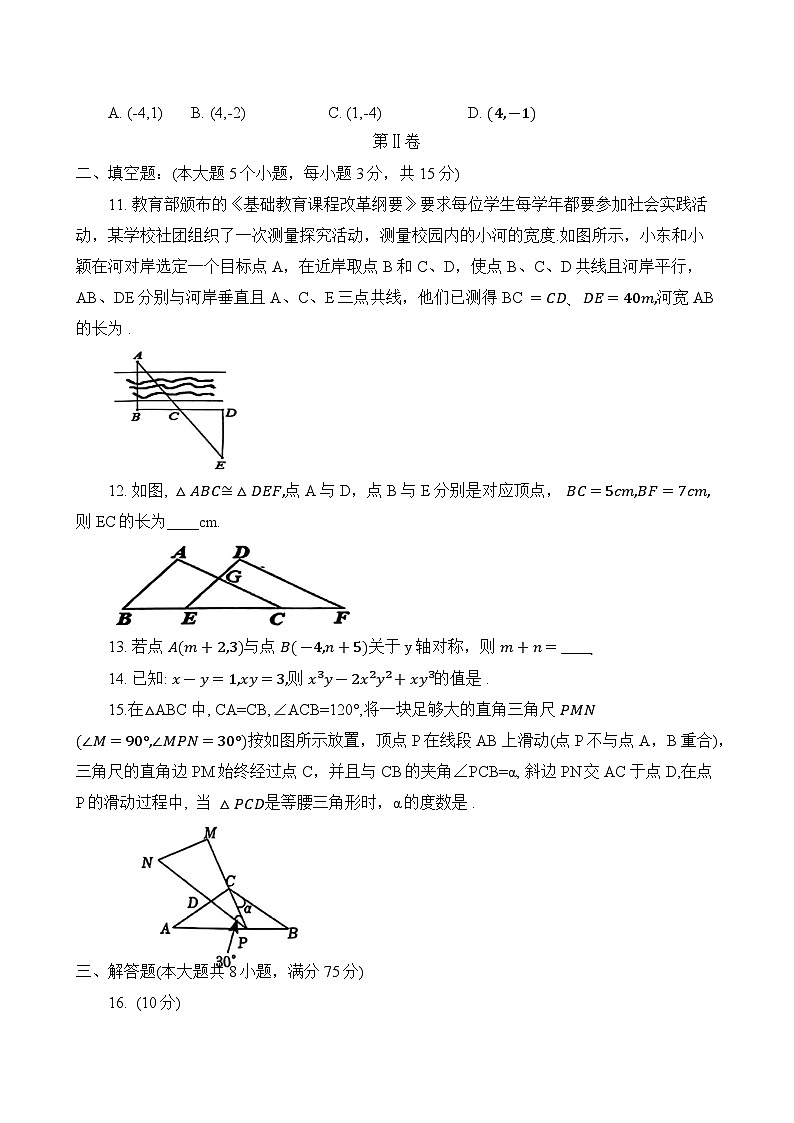
10. 如图, 在△ABC中, AB=AC, ∠BAC=90°, 若A(0,2),B(-3,-2), 则点C的坐标为 ( )
A. (-4,1) B. (4,-2)C. (1,-4) D. 4-1
第Ⅱ卷
二、填空题：(本大题5个小题，每小题3分，共15分)
11. 教育部颁布的《基础教育课程改革纲要》要求每位学生每学年都要参加社会实践活动，某学校社团组织了一次测量探究活动，测量校园内的小河的宽度.如图所示，小东和小颖在河对岸选定一个目标点A，在近岸取点B和C、D，使点B、C、D共线且河岸平行，AB、DE分别与河岸垂直且A、C、E三点共线，他们已测得BC =CD、DE=40m,河宽AB的长为 .
12. 如图, △ABC≅△DEF,点A与D，点B与E分别是对应顶点， BC=5cm,BF=7cm,则EC的长为____cm.
13. 若点 Am+23与点 B-4n+5关于y轴对称，则 m+n=_____.
14. 已知: x-y=1,xy=3,则 x³y-2x²y²+xy³的值是 .
15.在△ABC中, CA=CB,∠ACB=120°,将一块足够大的直角三角尺 PMN∠M=90°∠MPN=30°按如图所示放置，顶点P在线段AB上滑动(点P不与点A，B重合)，三角尺的直角边PM始终经过点C，并且与CB的夹角∠PCB=α, 斜边PN交AC于点D,在点P的滑动过程中, 当 △PCD是等腰三角形时，α的度数是 .
三、解答题(本大题共8小题，满分75分)
16. (10分)
(1) (5分) 计算: -12024+12-1+π-30;
(2) (5分) 化简: x-1²+x+2x-2-2x-3x-1.
17. (7分) 如图, △ABC和△ADE都是等腰三角形, BC、DE分别是这两个等腰三角形的底边,且∠BAC=∠DAE, 求证: BD=CE.
18. (8分) 解分式方程: x-3x-2+2=32-x.
19. (8分) 化简: 2xx+1-1÷x-1x2+2x+1.
20. (10分)为了推动绿色发展，促进人与自然和谐共生，某市加大了对山体的绿化.市绿化公司计划购买A、B两种小树苗.已知每棵A种小树苗比每棵B种小树苗的进价高20元，用800000元购进A种树木的数量和用600000元购买B种树木的数量相同.
(1) 求A、B两种小树苗每棵的单价分别是多少元?
(2) 预算资金为1700000元，其中800000元购买A种小树苗，其余资金购买B种小树苗，求A、B两种小树苗合计购买多少棵?
21. (10分) 如图，在长度为元1个单位长度的小正方形组成的正方形中，点A、B、C在小正方形的顶点上.
(1) 在图1中画出与△ABC关于直线l成轴对称的△A'B'C';
(2)如果三角形三个顶点都在格点处的三角形被称为“格点三角形”.那么请在图2中作出一个以AC为边与△ABC全等的格点三角形；
(3) 在图3中直线l上找一点P, 使PB+ PC的长最短.
22.(10分) 如图, 在△ABC中,∠C=90°, AC=12.
(1) 请用无刻度的直尺和圆规作出∠CAB的平分线(保留作图痕迹，不写作法)；
(2) 若(1) 中所作的角平分线与边BC交于点D, 过点D作DE⊥AB于点E.
①求证: AE =AC;
②若CD=4, S△ABD=30, 求BE的长.
23. (12分)
(1)如图1, 已知:在△ABC中,∠BAC=90°, AB=AC, 直线m经过点A,BD⊥直线m,CE⊥直线m, 垂足分别为点D、 E.求证DE=BD+ CE.
(2)如图2,将(1)中的条件改为: 在△ABC中, AB=AC,D、A、E三点都在直线m上, 并且有∠BDA=∠AEC=∠BAC=α，其中a为任意锐角或钝角.请问结论 DE=BD+CE是否成立? 如成立，请你给出证明； 若不成立，请说明理由.
(3) 如图3, D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合) , 点F为 ∠BAC平分线上的一点, 且△ABF和△ACF均为等边三角形, 连接BD、CE, 若 △DEF是等边三角形， ∠BDA=∠AEC=α,直接写出∠BAC的度数.
参考答案
选择题1-5CDDCB6-10AACBD
填空题
11.40
12.3
13.0
14.3
15.450或900
简答题
16.(1) 原式=-1+2+1=2
(2)原式=x2-2x+1+x2-4-2x2+3x+2x-3=3x-6
17.证明: ∵△ABC为等腰三角形,
∴AB=AC,
同理AD=AE .
∵∠ BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE .
在△ABD与△ACE中,
AB=AC
∠BAD=∠CAE
AD=AE
∴△ABD≌△ACE(SAS),
∴BD=CE .
18.解：去分母得:x-3+2x-2=-3,
解得：x=43,
检验：把x=43代入得：x-2≠0,
∴分式方程的解为x=43.
19.原式=2xx+1-x+1x+1÷x-1x+12=x-1x+1⋅x+12x-1=x+1,
20.解：(1)设A种零件的单价是x元，则B种零件的单价是(x-20)元,
依题意得：800000x=600000x-20.
解得x=80
经检验，x=80是原方程的解，且符合题意 .
则x-20=80-20=60(元)
答：A种零件的单价是80，则B种零件的单价是60元;
(2)800000÷80=10000, 1700000-800000=900000 900000÷60=15000
10000+15000=25000
答:A、B两种小树苗合计购买25000棵?
21.解：（1）如图，△AB′C′即为所求；
（2）如图所示，可以作3个；
（3）如图，点P即为所求．
22.（1）如图，AD为所求；
(2)①∵∠CAD=∠EAD,AD=AD , ∠C=90°,DE⊥AB
∴△CAD≌△EAD,∴AE =AC
②S△ABD=30=12AB∙DE,
∵△CAD≌△EAD,∴CD=DE=4,AC=AE=12
(AE+BE)∙DE=60（12+BE）=15 BE=3
23.证明:(1)∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠AEC=90°,
∵∠BAC=90°,∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,∴∠CAE=∠ABD,
在△ADB和△CEA中,∠ABD=∠CAE∠BDA=∠AEC,
∴△ADB≌△CEA(AAS),
∴BD=AE,AD=CE,∴DE=AE+AD=BD+CE;
(2)成立.
∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°-α,
∴∠CAE=∠ABD,
在△ADB和△CEA 中,∠ABD=∠CAE∠BDA=∠AEC,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE.
（3）结论：△DEF是等边三角形．
理由：如图3，由（2）可知，△ADB≌△CEA，
∴BD=AE，∠DBA=∠CAE，
∵△ABF和△ACF均为等边三角形，
∴∠ABF=∠CAF=60°，BF=AF，
∴∠DBA+∠ABF=∠CAE+∠CAF，即∠DBF=∠EAF，
在△DBF和△EAF中，
FB＝FA∠DBF＝∠EAFBD＝AE，
∴△DBF≌△EAF（SAS），
∴DF=EF，∠BFD=∠AFE，
∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°，
∴△DEF为等边三角形．
∵∠BDA=∠AEC=α∴∠BAC=α