2023-2024学年广东省深圳外国语学校八年级（下）期末数学试卷（含答案）

这是一份2023-2024学年广东省深圳外国语学校八年级（下）期末数学试卷（含答案），共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.若分式x2x−3有意义，则x的取值范围是( )
A. x>32B. x≠32C. x<32D. x=32
2.如图，在正方形网格中，两个阴影部分的格点三角形位似，则位似中心为( )
A. 点A
B. 点K
C. 点R
D. 点Q
3.如果方程(p−3)xp2−7−x+3=0是关于x的一元二次方程，则p的值是( )
A. 2B. −3C. 3D. ±3
4.如图，直线l1//l2//l3，直线AC依次交l1，l2，l3于点A，B，C，直线DF依次交l1，l2，l3于点D、E，F，若ABBC=34，DE=6，则EF的长为( )
A. 8
B. 5
C. 4
D. 2
5.两千四百多年前，我国学者墨子就在《墨经》中记载了小孔成像实验的做法与成因，图1是小孔成像实验图，抽象为数学问题如图2：AC与BD交于点O，AB/​/CD，若点O到AB的距离为10cm，点O到CD的距离为15cm，蜡烛火焰AB的高度是3cm，则蜡烛火焰倒立的像CD的高度是( )
A. 5cmB. 4.5cmC. 6.5cmD. 8cm
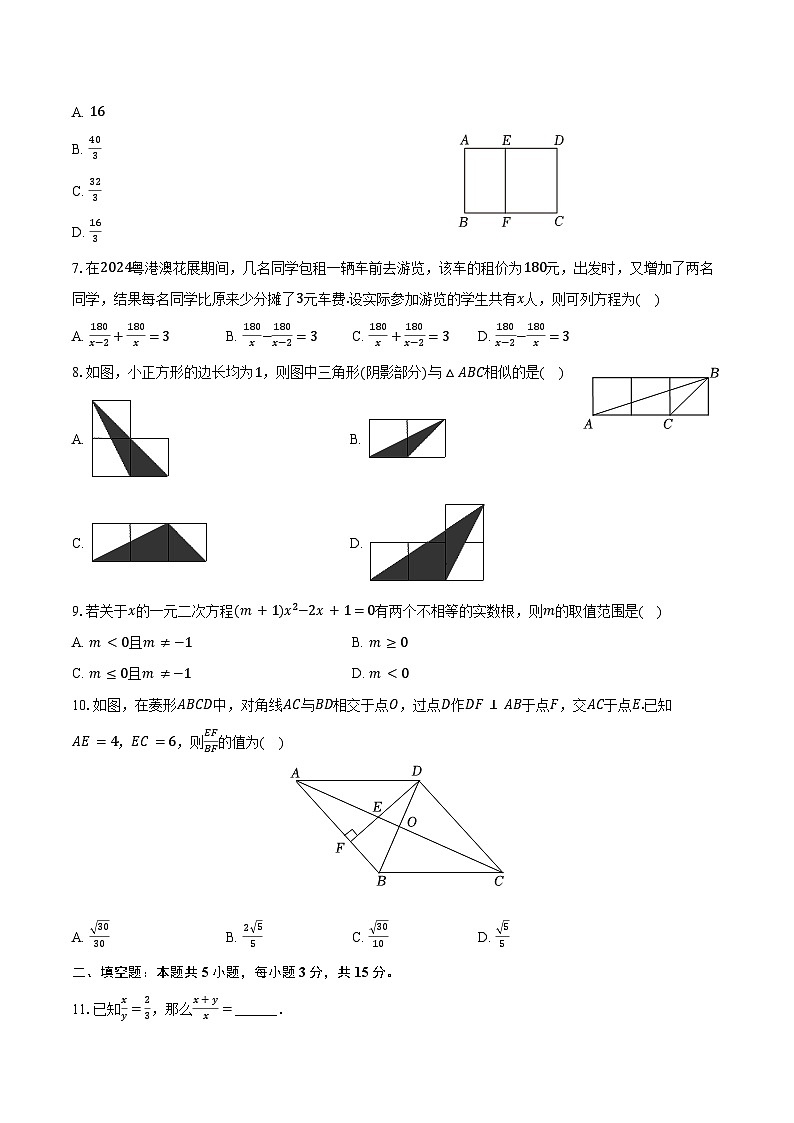
6.如图，在矩形ABCD中，AB=4，BC=6，点E，F分别在AD，BC上，且EF/​/AB，矩形ABCD与矩形BFEA相似，则矩形BFEA的面积为( )
A. 16
B. 403
C. 323
D. 163
7.在2024粤港澳花展期间，几名同学包租一辆车前去游览，该车的租价为180元，出发时，又增加了两名同学，结果每名同学比原来少分摊了3元车费.设实际参加游览的学生共有x人，则可列方程为( )
A. 180x−2+180x=3B. 180x−180x−2=3C. 180x+180x−2=3D. 180x−2−180x=3
8.如图，小正方形的边长均为1，则图中三角形(阴影部分)与△ABC相似的是( )
A. B.
C. D.
9.若关于x的一元二次方程(m+1)x2−2x+1=0有两个不相等的实数根，则m的取值范围是( )
A. m<0且m≠−1B. m≥0
C. m≤0且m≠−1D. m<0
10.如图，在菱形ABCD中，对角线AC与BD相交于点O，过点D作DF⊥AB于点F，交AC于点E.已知AE=4，EC=6，则EFBF的值为( )
A. 3030B. 2 55C. 3010D. 55
二、填空题：本题共5小题，每小题3分，共15分。
11.已知xy=23，那么x+yx=______．
12.已知关于x的方程x2+5x+m=0有一个根为−2，则m为______．
13.如图，正方形ABCD的边长为3，点E为AD边的中点，连接BD、CE，BD与CE相交于点F，则DF的长为______．
14.如图，在直角△ABC中，∠A=90°，AB=3，AC=4，正方形ADEF的顶点F，E，D分别在边AC，BC，AB上，若在△ABC内取一点，这点取自正方形ADEF的概率为______．
15.如图，在等腰Rt△ABC中，∠ACB=90°，P为BC边上的动点，CM⊥AP于点M，连接BM并延长交AC于点N，当N为AC边上中点时，若BC=4，则BP= ______．
三、解答题：本题共7小题，共55分。解答应写出文字说明，证明过程或演算步骤。
16.(本小题8分)
解方程：
①1x−3+x+13−x=1；
②(x−3)2−4=0．
17.(本小题6分)
先化简(1−1x+2)÷x2+2x+1x2−4，然后在−1，0，2中选一个你喜欢的x值，代入求值．
18.(本小题7分)
一个不透明的袋子中装有四个小球，这四个小球上各标有一个数字，分别是1，1，2，3.这些小球除标有的数字外都相同．
(1)从袋中机摸出一个小球，则摸出的这个小球上标有的数字是1的概率为______；
(2)先从袋中随机摸出一个小球，记下小球上标有的数字后，放回，摇匀，再从袋中随机摸出一个小球，记下小球上标有的数字，请利用画树状图或列表的方法、求摸出的这两个小球上标有的数字之积是偶数的概率．
19.(本小题8分)
某商场销售一种学生用的计算器，进价为每台20元，售价为每台30元，每周可卖160台.根据市场调查，发现如果每台计算器的售价每上涨1元，每周就会少卖10台，但厂家规定最高每台售价不能超过33元．
(1)设每台售价上涨x元，每周的销售量为y台，则y与x之间的函数关系式为______；
(2)当计算器售价为多少元时，商场每周的利润恰好为1680元？
20.(本小题8分)
如图，△ABC中，AB=2，BC=4，D为BC边上一点，BD=1．
(1)求证：△ABD∽△CBA；
(2)如果AD=52，求AC的长．
21.(本小题8分)
如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根，且其中一个根比另一个根大2，那么称这样的方程为“邻2根方程”.例如，一元二次方程x2+2x=0的两个根是x1=0，x2=−2，则方程x2+2x=0是“邻2根方程”.(1)通过计算，判断方程x2+9x+20=0是否是“邻2根方程”；
(2)已知关于x的一元二次方程x2−(m−1)x+3m−12=0(m是常数)是“邻2根方程”，求m的值．
22.(本小题10分)
已知四边形ABCD中，E、F分别是AB、AD边上的点，DE与CF交于点G．
【问题发现】
(1)如图1，若四边形ABCD是正方形，且DE⊥CF于G，则DECF= ______；
【拓展研究】
(2)如图2，当四边形ABCD是矩形时，且DE⊥CF于G，AB=m，AD=n，则DECF= ______；
【解决问题】
(3)老师上课时提出这样的问题：如图3，若四边形ABCD是平行四边形，且∠B+∠EGC=180°时，求证：DECF=ADCD；
小圳同学冥思苦想不得其解，提问到：在做题过程中，我先将DECF=ADCD转化成：DEAD=CFCD，发现△DEA与△CFD显然不相似，所以没办法直接得出DECF=ADCD，怎么办呢？
老师提示说：你是不是可以考虑引入一个桥梁或者考虑下添加辅助线来帮助解题呢？
同学们，请你帮助小圳同学解决此题，写出完整证明过程；
(4)如图4，若BA=BC=6，DA=DC=10，∠BAD=90°，DE⊥CF于G，请直接写出DECF的值．
参考答案
1.B
2.B
3.B
4.A
5.B
6.C
7.D
8.B
9.A
10.B
11.52
12.6
13. 2
14.2449
15.6−2 5
16.解：①1x−3+x+13−x=1
去分母得，1−(x+1)=x−3，
去括号得，1−x−1=x−3，
移项得，−x−x=−3−1+1，
合并同类项得，−2x=−3，
x的系数化为1得，x=32，
经检验，x=32是原分式方程的解；
②(x−3)2−4=0，
移项得，(x−3)2=4，
开方得，x−3=±2，
故x1=5，x2=1．
17.解：(1−1x+2)÷x2+2x+1x2−4
=x+2−1x+2⋅(x+2)(x−2)(x+1)2
=x+1x+2⋅(x+2)(x−2)(x+1)2
=x−2x+1，
∵x−2≠0，x+1≠0，
∴x≠2，−1，
∴当x=0时，原式=0−20+1=−2．
【答案】(1)12；
(2)树状图如下：
由上可得，一共有16种等可能性，其中两数之积是偶数的可能性有7种，
∴摸出的这两个小球上标有的数字之积是偶数的概率716．
【答案】(1)y=160−10x；
(2)由题意得：(30+x−20)(160−10x)=1680，
整理得：x2−6x+8=0，
解得：x1=2，x2=4，
当x=2时，30+x=32，符合题意；
当x=4时，30+x=34，不符合题意，舍去；
答：当计算器售价为32元时，商场每周的利润恰好为1680元．
20.(1)证明：∵在△ABC中，AB=2，BC=4，BD=1，
∴BDAB=ABBC=12，
∵∠ABD=∠CBA，
∴△ABD∽△CBA；
(2)由(1)知△ABD∽△CBA，
∴BDAB=ADAC，
∵AD=52，BC=4，AB=2，BD=1，
∴52AC=12，
∴AC=5．
21.解：(1)解方程x2+9x+20=0得：x=−4或x=−5，
∵−4−(−5)≠2，
∴x2+9x+20=0不是“邻2根方程”；
(2)由方程x2−(m−1)x+3m−12=0解得：x=m−4或x=3，
由于关于x的二次方程x2−(m−1)x+3m−12=0(m是常数)是“邻2根方程”，
则m−4−3=2或3−(m−4)=2，
解得m=9或5．
【答案】(1)1；
(2)nm；
(3)证明：∵四边形ABCD为平行四边形，
∴AD//|BC，AB/​/CD，
如图，在AD的延长线上取点M，使CM=CF，
则∠CMF=∠CFM，
∵AB/​/CD，
∴∠A=∠CDM，
∵AD/​/BC，
∴∠B+∠A=180°，
∵∠B+∠EGC=180°，∠EGF+∠EGC=180°，
∴∠B=∠EGF，
∴∠EGF+∠A=180°，
∴∠AED=∠CFM=∠CMF，
∴△ADE∽△DCM，
∴DECM=ADCD，即DECF=ADCD；
(4)解：过点C作CM⊥AB于点M，作CN⊥AD于点N，设CN=a，
∵∠BAD=90°，
∴四边形AMCN为矩形，BM=a−6，
∵BA=BC=6，DA=DC=10，BD为公共边，
∴△ABD≌△CBD(SSS)，
∴∠BCD=∠BAD=∠MCN=90°，
∴∠BCM=∠DCN，
∴△BCM∽△DCN，
∴CMCN=BCDC，即CMa=610，
∴CM=35a，
在Rt△BCM中，BM2+CM2=BC2，即(a−6)2+(35a)2=62，
解得a=0(舍去)或a=15017，
∴CN=15017，
∵∠BAD=90°，DE⊥CF，
∴∠BAD+∠EGF=180°，
∴∠AED+∠AFC=180°，
∴∠AEG=∠NFC，
∴Rt△ADE∽Rt△NCF，
∴DECF=ADNC=1015017=1715．