

2023-2024学年广东省大湾区高一下学期期末联合考试数学试题(含解析)
展开1.若复数z=1+i2+i,则z的模为( )
A. 2B. 5C. 3D. 10
2.已知向量a=1,2与向量b=k,k+1平行,则k=( )
A. 1B. 0C. −1D. −2
3.设△ABC的内角A,B,C所对的边分别为a,b,c,若a= 3,b=1,A=60∘,则B等于( )
A. 30∘B. 30∘或150∘C. 60∘D. 150∘
4.已知空间两条不同的直线m,n和两个不同的平面α,β,则下列命题中正确的是( )
A. 若m//α,n⊂α,则m//n
B. 若α∩β=m,m⊥n,则n⊥α
C. 若m//α,n//α,则m//n
D. 若m//α,m⊂β,α∩β=n,则m//n
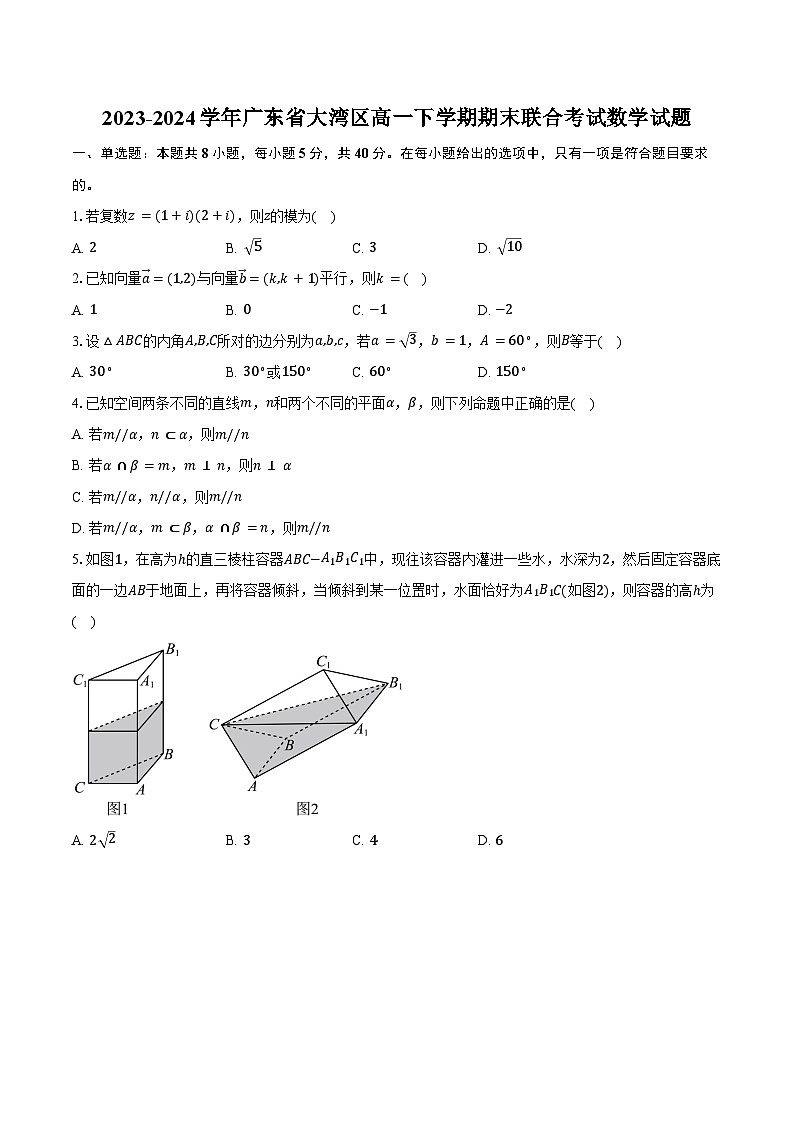
5.如图1,在高为ℎ的直三棱柱容器ABC−A1B1C1中,现往该容器内灌进一些水,水深为2,然后固定容器底面的一边AB于地面上,再将容器倾斜,当倾斜到某一位置时,水面恰好为A1B1C(如图2),则容器的高ℎ为( )
A. 2 2B. 3C. 4D. 6
6.已知扇形AOB的半径为13,以O为原点建立如图所示的平面直角坐标系,OA=13,0,OB=12,5,弧AB的中点为C,则OC=( )
A. 3 13,2 13B. 52 26,12 26C. 4 10,3D. 153,4
7.将函数y=sin2x的图象向左平移φ个单位长度后,得到函数y=cs(2x+π3)的图象,则φ的值可以是( )
A. 7π12B. 5π12C. π12D. π3
8.如图:正方体ABCD−A1B1C1D1的棱长为2,E为DD1的中点,过点D作正方体截面使其与平面A1EC1平行,则该截面的面积为( )
A. 2 3B. 2 6C. 4 6D. 4 3
二、多选题:本题共3小题,共15分。在每小题给出的选项中,有多项符合题目要求。
9.已知z1=2−i,z2为复数,则( )
A. 存在唯一的z2,使 |z1z2|=5 B. 存在唯一的z2,使z1z2=5
C. 存在唯一的z2,使z1+z2=4D. 存在唯一的z2,使z1z2+z1+z2=9
10.如图,ABCD是底面直径为2高为1的圆柱OO1的轴截面,四边形OO1DA绕OO1逆时针旋转θ0≤θ≤π到OO1D1A1,则( )
A. 圆柱OO1的侧面积为4π
B. 当0<θ<π时,DD1⊥A1C
C. 当θ=π3时,异面直线A1D与OO1所成的角为π4
D. ▵A1CD面积的最大值为 3
11.直角ΔABC中,斜边AB=2,P为ΔABC所在平面内一点,AP=12sin2θ⋅AB+cs2θ⋅AC(其中θ∈R),则( )
A. AB⋅AC的取值范围是(0,4)
B. 点P经过ΔABC的外心
C. 点P所在轨迹的长度为2
D. PC⋅(PA+PB)的取值范围是−12,0
三、填空题:本题共3小题,每小题5分,共15分。
12.已知圆锥的轴截面是边长为2的等边三角形,则此圆锥的表面积为 .
13.计算:2sinπ18−csπ92sinπ9= .
14.已知对任意平面向量AB=x,y,把AB绕其起点A沿逆时针方向旋转θ角得到向量AP=(xcsθ−ysinθ,xsinθ+ycsθ),叫做把点B绕点A沿逆时针方向旋转θ角得到点P.已知平面内点A1,2,点B1+ 2,2−2 2,把点B绕点A沿逆时针方向旋转π4角得到点P,则点P的坐标为 .
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题12分)
在四棱锥P−ABCD中,底面ABCD为直角梯形,BC//AD,∠ADC=90∘,E,F分别为线段AD,PC的中点,PE⊥底面ABCD,BC=CD=12AD=12PE=1.
(1)作出平面BEF与平面PCD的交线l,并证明l//BE;
(2)求点C到平面FBE的距离.
16.(本小题12分)
如图,△ABC是等边三角形,D是BC边上的动点(含端点),记∠BAD=α,∠ADC=β.
(1)求2csα−csβ的最大值;
(2)若BD=1,csβ=17,求△ABD的面积.
17.(本小题12分)
人脸识别技术在各行各业的应用改变着人类的生活,所谓人脸识别,就是利用计算机分析人脸视频或者图像,并从中提取出有效的识别信息,最终判别对象的身份,在人脸识别中为了检测样本之间的相似度主要应用距离的测试,常用测量距离的方式有曼哈顿距离和余弦距离.若二维空间有两个点Ax1,y1,Bx2,y2,则曼哈顿距离为:dA,B=x1−x2+y1−y2,余弦相似度为:csA,B=x1 x12+y12×x2 x22+y22+y1 x12+y12×y2 x22+y22,余弦距离为1−csA,B
(1)若A−1,2,B35,45,求A,B之间的曼哈顿距离dA,B和余弦距离;
(2)已知Msinα,csα,Nsinβ,csβ,Qsinβ,−csβ,若csM,N=15,csM,Q=25,求tanαtanβ的值
(3)已知0<α<β<π2,M5csα,5sinα、N13csβ,13sinβ,P5csα+β,5sinα+β,若csM,P=513,csM,N=6365,求M、P之间的曼哈顿距离.
18.(本小题12分)
已知平行四边形ABCD中,DE=2EC,AF+DF=0,AE和BF交于点P.
(1)试用AB,AD表示向量AP.
(2)若▵BPE的面积为S1,▵APF的面积为S2,求S1S2的值.
(3)若AB+AD=AB−AD,AC⋅BD=0,求∠APF的余弦值.
19.(本小题12分)
如图,三棱台ABC−A1B1C1中,AB=AC= 5,B1C1=2BC=2 2,AA1=2 6,点A在平面A1B1C1上的射影在∠B1A1C1的平分线上.
(1)求证:AA1⊥B1C1;
(2)若A到平面A1B1C1的距离为4,求直线AC与平面AA1B1B所成角的正弦值.
答案解析
1.D
【解析】由复数z=1+i2+i=1+3i,所以z= 12+32= 10.
故选:D.
2.A
【解析】因为向量a=1,2与向量b=k,k+1平行,所以1×k+1=2k,解得k=1.
故选:A
3.A
【解析】解:由正弦定理可得sinB=basinA=1 3sin60∘=1 3× 32=12,
由a= 3,b=1,可得a>b,则A>B,故B<60∘,
又sinB=12,则B=30∘.
故选:A.
4.D
【解析】对选项A:若m//α,n⊂α,则m//n或m,n为异面直线,错误;
对选项B:若α∩β=m,m⊥n,则n和α可以是任何位置关系,错误;
对选项C:若m//α,n//α,则n和m可以是任何位置关系,错误;
对选项D:若m//α,m⊂β,α∩β=n,则m//n,正确;
故选:D.
5.B
【解析】解:在图(1)中的几何体中,水的体积为V1=S▵ABC×2=2S▵ABC,
在图(2)的几何体中,水的体积为:V2=V ABC−A1B1C1−VC−A1B1C1=S▵ABC×ℎ−13×S ▵A1B1C1×ℎ=23S▵ABCℎ,
因为V1=V2,可得23S▵ABCℎ=2S▵ABC,解得ℎ=3.
故选:B.
6.B
【解析】因为csOA,OB=OA⋅OBOA⋅OB=13,0⋅12,513× 144+25=1213,
故csOA,OC= 1+csOA,OB2= 2526=5 2626,
故xC=13csOA,OC=5 262,
故yC= 132−5 2622= 262,故OC=52 26,12 26.
故选:B
7.B
【解析】因为y=cs(2x+π3)=sin(2x+5π6).
将函数y=sin2x的图象向左平移φ个单位长度后,得到函数y=sin(2x+2φ)的图象,
所以有sin(2x+2φ)=sin(2x+5π6),所以2φ+2kπ=5π6,k∈Z,
所以有,φ=5π12−kπ,k∈Z.
对于A项,令φ=7π12,即5π12−kπ=7π12,解得k=−16∉Z,A项错误;
对于B项,令φ=5π12,即5π12−kπ=5π12,解得k=0∈Z,B项正确;
对于C项,令φ=π12,即5π12−kπ=π12,解得k=13∉Z,C项错误;
对于D项,令φ=π3,即5π12−kπ=π3,解得k=112∉Z,D项错误
故选:B.
8.B
【解析】根据题意,取AA1,CC1的中点分别为M,N,连接DM,DN,B1M,B1N,MN,如下图所示:
易知DE=C1N=1,且DE//C1N,所以四边形DEC1N是平行四边形;
即DN//EC1,又DN⊄平面A1EC1,EC1⊂平面A1EC1,
所以DN//平面A1EC1;
同理可得DM//平面A1EC1;
DN∩DM=D,DN,DM⊂平面DMN,
所以平面DMN//平面A1EC1平行,
即过点D作正方体截面使其与平面A1EC1平行的截面即为平面DMN;
显然A1E//B1N,A1E=B1N= 5,且DM//A1E,A1E=DM= 5;
所以四边形DMB1N是边长为 5的菱形,即所求截面面积即为菱形DMB1N的面积;
易知MN=2 2,B1D=2 3,所以其面积为12MN⋅B1D=12×2 2×2 3=2 6.
故选:B
9.BCD
【解析】解:设z2=a+bi,a,b均为实数,
则z1z2=(2−i)(a+bi)=2a+b+(2b−a)i,
对于A,|z1z2|=5时,(2a+b)2+(2b−a)2=25,
化简得,a2+b2=5,有无数组解,故选项A错误;
对于B,z1z2=5时,2a+b+(2b−a)i=5,
所以2a+b=52b−a=0,解得a=2b=1,有唯一解,故选项B正确;
对于C,z1+z2=4时,z2=4−z1=4−(2−i)=2+i,存在唯一解,故选项C正确;
对于D,z1z2+z1+z2=9,
即2a+b+(2b−a)i+2−i+a+bi=(3a+b+2)+(3b−a−1)i=9,
所以3a+b+2=93b−a−1=0,
解得a=2b=1,有唯一解,故选项D正确.
故选:BCD.
10.BC
【解析】对于A,圆柱OO1的侧面积为2π×1×1=2π, A错误;
对于B,因为0<θ<π,所以DD1⊥D1C,又DD1⊥A1D1,
所以DD1⊥平面A1D1C,所以DD1⊥A1C, B正确;
对于C,因为A1D1//OO1,所以∠DA1D1就是异面直线A1D与OO1
所成的角,因为∠DO1D1=π3,所以▵DO1D1为正三角形,
所以DD1=A1D1=1,因为A1D1⊥DD1,所以∠DA1D1=π4, C正确;
对于D,作D1E⊥DC,垂足为E,连接A1E,所以DC⊥平面A1D1E,所以A1E⊥DC.
在Rt▵A1D1E中,A1E= A1D12+ED12= 1+D1E2≤ 1+D1O12= 2,
S▵A1CD=12×DC×A1E≤12×2× 2= 2,所以S▵A1CDmax= 2, D错误.
故选:BC.
11.ABD
【解析】解:由AB⋅AC=AC2,又斜边AB=2,则|AC|∈(0,2),则AB⋅AC∈(0,4),A正确;
若O为AB中点,则AO=12AB,故AP=sin2θ⋅AO+cs2θ⋅AC,又sin2θ+cs2θ=1,
所以O,P,C共线,故P在线段OC上,轨迹长为1,又O是△ABC的外心,B正确,C错误;
由上PA+PB=2PO,则PC⋅(PA+PB)=2PC⋅PO=−2|PC||PO|,
又|PC|+|PO|=|OC|=1,则|PC||PO|≤(|PC|+|PO|22)2=14,
当且仅当|PC|=|PO|=12等号成立,
所以PC⋅(PA+PB)=−2|PC||PO|∈[−12,0],D正确.
故选ABD.
12.3π
【解析】∵圆锥轴截面是边长为2的等边三角形,∴圆锥底面半径r=1,圆锥母线长l=2,
∴圆锥的表面积S=πrl+πr2=2π+π=3π.
故答案为:3π.
13.− 32或−12 3
【解析】2sinπ18−csπ92sinπ9
=2sinπ6−π9−csπ92sinπ9
=2sinπ6csπ9−2csπ6sinπ9−csπ92sinπ9
=−csπ6=− 32.
故答案为:− 32.
14.(4,1)
【解析】解:AB=( 2,−2 2),
AP=( 2cs π4−(−2 2)sin π4, 2sin π4+(−2 2)cs π4)=(3,−1)
OP=OA+AP=(1,2)+(3,−1)=(4,1),
所以P点坐标为P(4,1).
故答案为(4,1)
15.(1)
在图形中作出交线l
∵BC//AD,且E为AD中点,BC=12AD
∴BC//DE且BC=DE
∴四边形BCDE为平行四边形
∴BE//CD,∵BE⊄面PCD,CD⊂面PCD,
∴BE//面PCD
又BE⊂面BEF,面BEF∩面PCD=l,
∴BE//l
(2)
设点C到平面FBE的距离为ℎ,l∩PD=G,连接GE,
∵F为PC中点,∴G为PD中点,∴GE=12PA
∵BE//CD,∠ADC=90∘,∴BE⊥AD,
∵PE⊥平面ABCD,∴PE⊥BE
∵PE∩AD=E,∴BE⊥平面PAD,∴BE⊥EG.
∵VC−BEF=VF−BCE=VG−BCE=VG−BED
∴13S▵BEF⋅ℎ=13S▵BED⋅12PE
∴12BE⋅GE⋅ℎ=12BE⋅DE
∴ℎ=DEGE=1 52=2 55
【解析】(1)先利用线面平行的判定定理可证得BE//面PCD,再由线面平行的性质定理可证得结论,
(2)利用等体积VC−BEF=VF−BCE=VG−BCE=VG−BED求解即可
16.解:(1)由△ABC是等边三角形,得β=α+π3,0≤α≤π3,
故2cs α−cs β=2cs α−cs(α+π3)
=32csα+ 32sinα= 3sin(α+π3),
故当α=π6,即D为BC中点时,原式取最大值 3.
(2)由cs β=17,得sin β=4 37,
故sin α=sin(β−π3)=sin βcs π3−cs βsin π3=3 314,
由正弦定理ABsin∠ADB=BDsin∠BAD,
故AB=sinβsinαBD=83,
故S△ABD=12AB⋅BD⋅sin B=12×83×1× 32=2 33.
【解析】(1)求出β=α+π3,0≤α≤π3,根据三角函数的运算性质求出其最大值即可;
(2)根据正弦定理求出AB的值,从而求出三角形的面积即可.
17.(1)
dA,B=−1−35+2−45=145,
csA,B=−1 5×35+2 5×45= 55,故余弦距离等于1−csA,B=1− 55;
(2)
csM,N=sinα sin2α+cs2α⋅sinβ sin2β+cs2β+csα sin2α+cs2α⋅csβ sin2β+cs2β=sinαsinβ+csαcsβ=15;
csM,Q=sinα sin2α+cs2α⋅sinβ sin2β+cs2β+csα sin2α+cs2α⋅−csβ sin2β+cs2β=sinαsinβ−csαcsβ=25
故sinαsinβ=310,csαcsβ=−110,则tanαtanβ=sinαsinβcsαcsβ=−3.
(3)
因为 5sinα2+5csα2=5, 5sinα+β2+5csα+β2=5,
所以csM,P=5csα5×5csα+β5+5sinα5×5sinα+β5=csβ=513.
因为0<β<π2,所以sinβ= 1−cs2β=1213.
因为 13sinα2+13csα2=13,
所以csM,N=5csα5×13csβ13+5sinα5×13sinβ13=csα−β=6365.
因为0<α<β<π2,则−π2<α−β<0,
所以sinα−β=− 1−cs2α−β=−1665.
因为csα=csα−β+β=csα−βcsβ−sinα−βsinβ=35,
sinα= 1−cs2α=45,所以M3,4.
因为csα+β=csαcsβ−sinαsinβ=−3365,
sinα+β=sinαcsβ+csαsinβ=5665,
所以P−3313,5613.
因为3−−3313+4−5613=7213+413=7613,
所以M、P之间的曼哈顿距离是7613.
【解析】(1)根据公式直接计算即可.
(2)根据公式得到sinαsinβ+csαcsβ=15,sinαsinβ−csαcsβ=25,计算得到答案.
(3)利用两角和与差的正弦、余弦公式可求出点M、P的坐标,结合题中定义可求得M、P之间的曼哈顿距离.
18.(1)解:∵点P在BF上,∴AP=xAF+1−xAB=x2AD+1−xAB
又∵AE=AD+23AB,AP//AE,
∴x2=1−x23,解得x=34,∴AP=14AB+38AD.
(2)解:由(1)可得AP=38AE,∴APAE=38,即APPE=35
∵AP=14AB+34AF,14+34AP=14AB+34AF
∴BP=3PF,BPPF=3,∴S1S2=S▵BPES▵APF=BP⋅PEPF⋅AP=5.
(3)解:由AB+AD=AB−AD,所以AB+AD2=AB−AD2,
即AB2+2AB⋅AD+AD2=AB2−2AB⋅AD+AD2,所以4AB⋅AD=0,即AB⊥AD,
又AC⋅BD=0,所以平行四边形ABCD是正方形,如图所示的建系
则∠APF是向量AE和FB的夹角,不妨设AB=1,AE=23,1,FB=1,−12
∴cs ⟨AE,FB⟩=AE⋅FB|AE|⋅|FB|= 6565,∴∠APF的余弦值是 6565.
【解析】(1)根据平面向量共线定理的推论得到AP=xAF+(1−x)AB,再由AE=AD+23AB且AP//AE,即可得到方程,求出x,即可得解;
(2)由(1)得到线段的比,即可得到面积之比;
(3)依题意可得平行四边形ABCD是正方形,建立平面直角坐标系,利用坐标法求出两向量夹角的余弦值,即可得解;
19.解:(1)(1)证明:设点A在平面A1B1C1上的射影为O,
则点O在∠B1A1C1的平分线A1D上,
所以AO⊥平面A1B1C1,因为B1C1⊂平面A1B1C1,所以AO⊥B1C1,
因为AB=AC,△ABC∽△A1B1C1,所以A1B1=A1C1,所以A1D⊥B1C1,
又因为AO∩A1D=O,AO⊂平面AA1O
所以B1C1⊥平面AA1O,又因为AA1⊂平面AA1O,所以AA1⊥B1C1;
(2)以O为原点,OD所在直线为y轴,OA所在直线为z轴,建立空间直角坐标系,如图所示:
因为A到平面A1B1C1的距离为4,所以A(0,0,4),
A1O= AA12−AO2= (2 6)2−42=2 2,
所以A1(0,−2 2,0),
由已知得B1C1=2BC=2 2,结合△ABC∽△A1B1C1,及(1)中A1B1=A1C1,
得A1B1=A1C1=2AB=2 5,
所以A1D= (2 5)2−( 2)2=3 2,所以OD= 2,
所以B1( 2, 2,0),C1(− 2, 2,0),所以AC=12A1C1=(− 22,3 22,0),
A1A=(0,2 2,4),A1B1=( 2,3 2,0),
设平面AA1B1B的一个法向量为n=(x,y,z),
则n•A1A=0n•A1B1=0,即2 2y+4z=0 2x+3 2y=0,令y=−1,得x=3,z= 22,
所以n=(3,−1, 22),设直线AC与平面AA1B1B所成的角为θ,
则sinθ=|cs
=−3 22−3 22+0 9+1+0× 12+92+0=2 10535,
所以直线 AC 与平面 AA1B1B 所成角的正弦值为 2 10535 .
【解析】(1)利用线面垂直证线线垂直即可;
(2)建立空间直角坐标系,利用空间向量进行求解.
2023-2024学年广东省大湾区高一下学期期末联合考试数学试题(含答案): 这是一份2023-2024学年广东省大湾区高一下学期期末联合考试数学试题(含答案),共11页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
广东省大湾区2023-2024学年高二下学期期末联合考试数学试题: 这是一份广东省大湾区2023-2024学年高二下学期期末联合考试数学试题,共6页。
广东省大湾区2023-2024学年高一下学期期末联合考试数学试题(解析版): 这是一份广东省大湾区2023-2024学年高一下学期期末联合考试数学试题(解析版),共19页。












