初中数学3 正方形的性质与判定教案配套课件ppt

这是一份初中数学3 正方形的性质与判定教案配套课件ppt，共28页。
1. 下列性质中，正方形具有但菱形却不一定具有的性质是 （　C　）
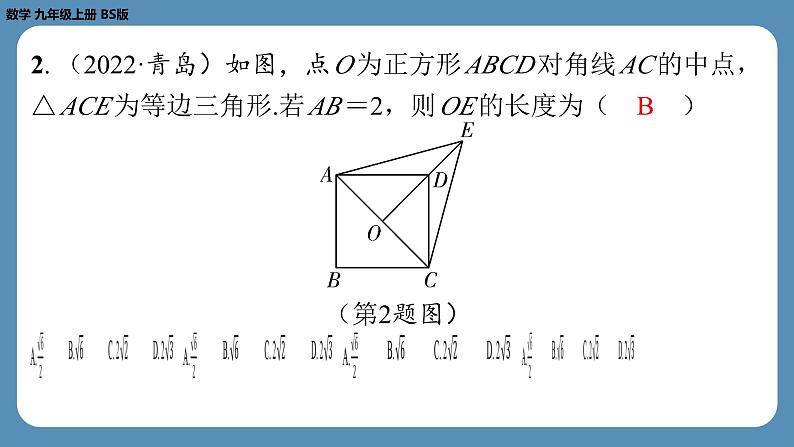
2. （2022·青岛）如图，点 O 为正方形 ABCD 对角线 AC 的中点， △ ACE 为等边三角形.若 AB ＝2，则 OE 的长度为（　B　）
3. （2022·黔东南）如图，在边长为2的等边三角形 ABC 的外侧 作正方形 ABED ，过点 D 作 DF ⊥ BC ，垂足为 F ，则 DF 的长为 （　D　）
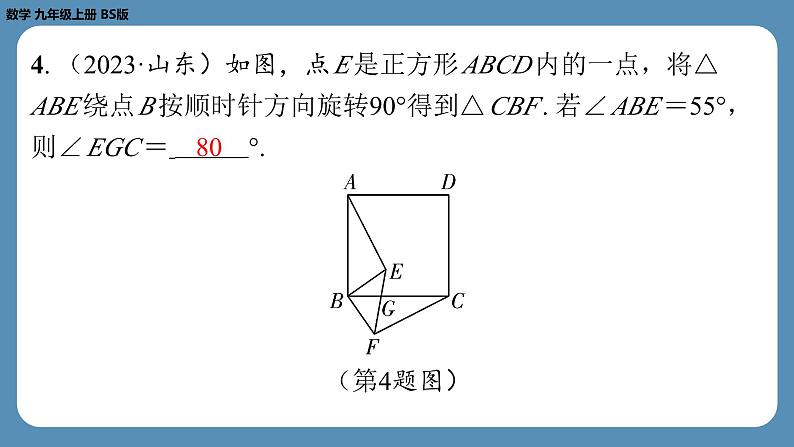
4. （2023·山东）如图，点 E 是正方形 ABCD 内的一点，将△ ABE 绕点 B 按顺时针方向旋转90°得到△ CBF . 若∠ ABE ＝55°， 则∠ EGC ＝ ⁠°.
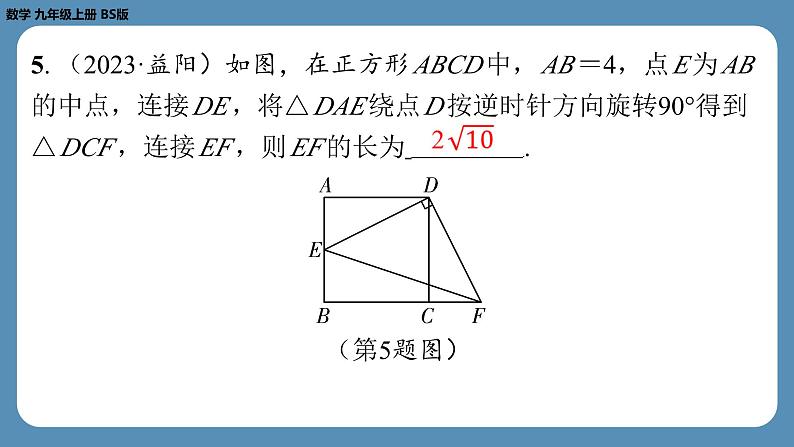
5. （2023·益阳）如图，在正方形 ABCD 中， AB ＝4，点 E 为 AB 的中点，连接 DE ，将△ DAE 绕点 D 按逆时针方向旋转90°得到 △ DCF ，连接 EF ，则 EF 的长为 ⁠.
7. 如图，已知点 E 是正方形 ABCD 外一点， AE ＝ AD ，∠ ADE ＝75°，求∠ AEB 的度数.
8. 如图，在正方形 ABCD 中，已知点 E 是 AB 上一点，点 F 是 AD 延长线上一点，且 CE ＝ CF . （1）求证： BE ＝ DF ；
（2）连接 EF ，若 CE ＝5，求 EF 的长.
9. （2023·内江）如图，已知四边形 ABCD 是边长为4的正方形， △ BPC 是等边三角形，则阴影部分的面积为 ⁠.
11. 如图，在正方形 ABCD 中， G 是对角线 BD 上的一点， GE ⊥ CD 于点 E ， GF ⊥ BC 于点 F ，连接 AG ， EF . （1）求证： AG ＝ EF ；
（2）若∠ DAG ＝30°， GE ＝1，求正方形 ABCD 的面积.
12. 如图，已知点 D 在边 CG 上，四边形 ABCD 和 CEFG 均为正 方形，点 H 是 AF 的中点.求证：（1） BG ＝ DE ；
13. （选做）在边长为5的正方形 ABCD 中，点 E 在边 CD 所在直 线上，连接 BE ，以 BE 为边，在 BE 的下方作正方形 BEFG ，并 连接 AG . （1）如图1，当点 D ， E 重合时，则 AG ＝ ⁠；
（2）如图2，当点 E 在线段 CD 上时，若 DE ＝2，求 AG 的长；