2024-2025学年度北师版八上数学-第十周自主评价练习（课件）

这是一份2024-2025学年度北师版八上数学-第十周自主评价练习（课件），共35页。

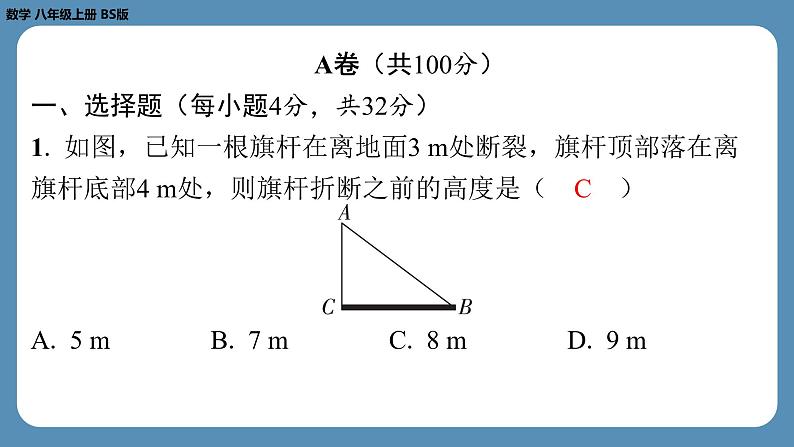
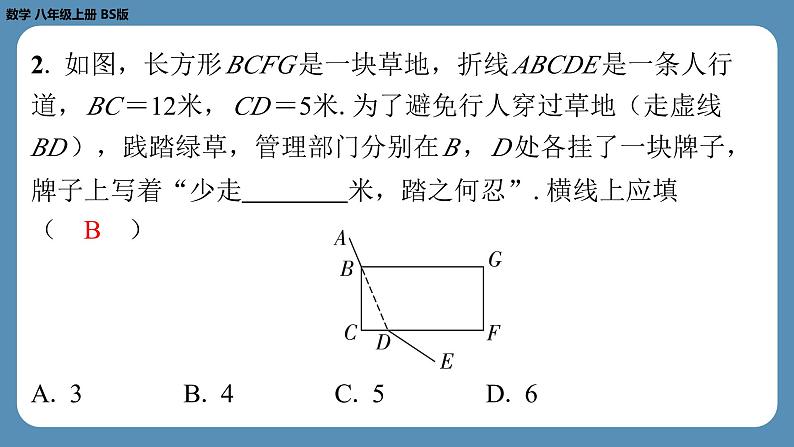
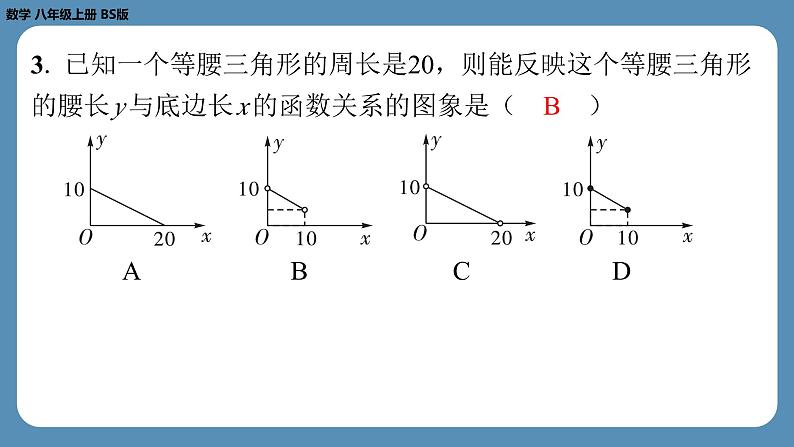
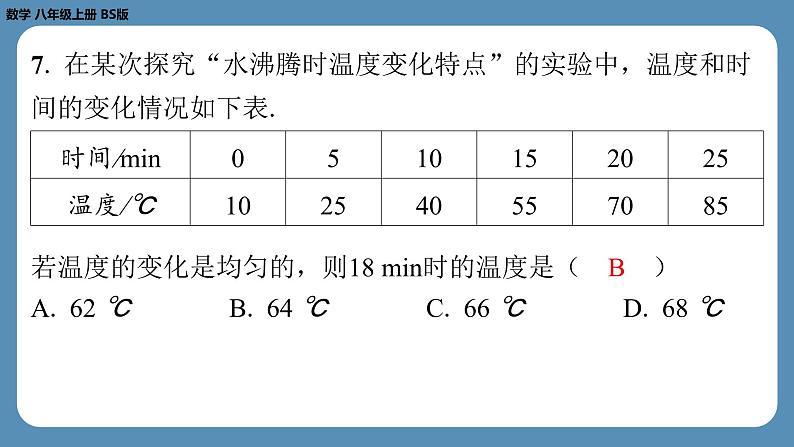
第十周自主评价练习（专题练习） 【1.3勾股定理的应用及4.4一次函数的应用】A卷（共100分）一、选择题（每小题4分，共32分）1. 如图，已知一根旗杆在离地面3 m处断裂，旗杆顶部落在离旗杆底部4 m处，则旗杆折断之前的高度是（　C　）C2. 如图，长方形 BCFG 是一块草地，折线 ABCDE 是一条人行道， BC ＝12米， CD ＝5米.为了避免行人穿过草地（走虚线 BD ），践踏绿草，管理部门分别在 B ， D 处各挂了一块牌子，牌子上写着“少走 　　　　米，踏之何忍”.横线上应填（　B　）B3. 已知一个等腰三角形的周长是20，则能反映这个等腰三角形的腰长 y 与底边长 x 的函数关系的图象是（　B　）ABCDB4. 若用长为50的栏杆围成一个长为 x ，宽为 y 的长方形，则 y 与 x 的函数表达式为（　A　）A5. 如图，有一个正方体盒子，棱长为1 cm.若一只蚂蚁要从盒底的点 A 沿盒子的表面爬到盒顶的点 B ，则蚂蚁爬行的最短路程是（　D　）D6. 若弹簧的长度 y （cm）与所挂物体的质量 x （kg）的关系如图所示，则弹簧所挂物体质量为2 kg时的长度是（　D　）D7. 在某次探究“水沸腾时温度变化特点”的实验中，温度和时间的变化情况如下表.若温度的变化是均匀的，则18 min时的温度是（　B　）B8. 某生物小组观察一植物生长，得到植物高度 y （cm）与观察时间 x （天）的关系，并画出如图所示的图象，下列说法错误的是（　A　）A二、填空题（每小题4分，共20分）9. 已知一个三角形的底边长为4，高为 x ，面积为 y ，则 y 与 x 之间的关系式为 ⁠.10. 下列表格是一项实验的统计数据（单位：cm）.当它表示篮球从一定高度落下时，弹跳高度 y 是下落高度 x 的一次函数，则 y 与 x 之间的关系式为 ⁠.y ＝2 x 　 11. 如图，已知圆柱的底面周长为16， BC ＝12，动点 P 从点 A 出发，沿着圆柱的侧面运动到 BC 的中点 S ，则运动的最短路程为 ⁠.10　12. 已知一水池现蓄水20m3，用水管以15m3/h的速度向水池中注水，则水池蓄水量 y （m3）与注水时间 x （h）之间的关系式是 ⁠.y ＝15 x ＋20　13. 甲、乙两人进行比赛，甲比乙跑得快，现在甲让乙先跑10 m，甲再起跑.如图， l1和 l2分别表示甲、乙两人跑步的路程 y （m）与甲跑步的时间 x （s）之间的函数关系，其中 l1的函数表达式为 y1＝8 x .甲追上乙用了 s.5　三、解答题（本大题共5小题，共48分）14. （本小题满分12分，每题6分）（1）如图，小明准备测量一段水渠的深度，他把一根竹竿 AB 竖直插到水底，此时竹竿 AB 离岸边点 C 处的水平距离 CD ＝1.5 m，竹竿高出水面的部分 AD 长0.5 m.若把竹竿的顶端 A 拉到岸边点 C 处，竿顶和岸边的水面刚好相齐，则水渠的深度 BD 为多少米？解：设 BD ＝ x m，则 AB ＝ BC ＝（ x ＋0.5）m.在Rt△ CDB 中，由勾股定理，得1.52＋ x2＝（ x ＋0.5）2， 解得 x ＝2.故水渠的深度 BD 为2 m.（2）如图，甲、乙两条渔船从港口 O 同时出发，甲渔船以8 n mile/h的速度向东北方向航行，乙渔船以6 n mile/h的速度向西北方向航行.一个半小时后，甲、乙两条渔船相距多少海里？ 15. （本小题满分8分）根据市卫生防疫部门的要求，游泳池必须定期换水后才能对外开放.在换水时需要经“排水—清洗—注水”的过程.某游泳馆从8：00开始对游泳池进行换水，已知该游泳池的排水速度是注水速度的2倍，其中游泳池内剩余的水量 y （m3）与换水时间 x （h）之间的函数图象如图所示.根据图象解答下列问题：（1）该游泳池清洗需要 h；（2）求排水过程中 y 与 x 之间的函数关系式，并写出自变量 x 的取值范围；1.2　（3）求该游泳馆换水结束的时间.解：（2）设排水过程中 y （m3）与 x （h）之间的函数关系式为 y ＝ kx ＋ b .由题意，得 b ＝1 200，1.5 k ＋ b ＝0，解得 k ＝－800.所以排水过程中 y 与 x 之间的函数关系式为 y ＝－800 x ＋1 200（0≤ x ≤1.5）.（3）由题意，得排水的速度为1 200÷1.5＝800（m3/h）.所以注水的速度为800÷2＝400（m3/h）.所以注水的时间为1200÷400＝3（h）.因为8＋2.7＋3＝13.7（h）＝13：42，所以该游泳馆在13：42换水结束.16. （本小题满分8分）如图，一架长25 m的云梯斜靠在一面墙上，梯子底端 C 离墙角 B 的距离为7 m.（1）这架梯子的顶端 A 距地面有多高？（2）若梯子的顶端 A 下滑了4 m，则梯子的底端在水平方向滑动了多少米？  17. （本小题满分10分）某同学通过查阅资料发现声音在空气中传播的速度和气温存在如下的关系：（1）若声音在空气中的传播速度 y （m/s）是气温 x （℃）的一次函数，求 y 与 x 之间的函数关系式；（2）当日气温为17℃，小明看到烟花燃放5s后才听到声响，则小明与燃放烟花所在地大约相距多远？  18. （本小题满分10分）1号探测气球从海拔10m处出发，以1m/min的速度竖直上升，与此同时，2号探测气球从海拔20m处出发，以 a m/min的速度竖直上升.两个气球都上升了60min，1号、2号气球所在位置的海拔 y1， y2（m）与上升时间 x （min）的函数关系如图所示.请根据图象回答下列问题：（1） b ＝ ⁠；（2）请求出 y2与 x 之间的函数关系式；30　（3）当上升多长时间时，两个气球的海拔差为5m？解：（2）设 y2＝ ax ＋20.因为 y2＝ ax ＋20过点（20，30），所以30＝20 a ＋20，解得 a ＝0.5.所以 y2与 x 之间的函数关系式为 y2＝0.5 x ＋20.（3）由题意，得 y1＝ x ＋10.①2号气球比1号气球高5m时，则有（0.5 x ＋20）－（ x ＋10）＝5，解得 x ＝10；②1号气球比2号气球高5m时，则有（ x ＋10）－（0.5 x ＋20）＝5，解得 x ＝30.故上升了10min或30min后两个气球的海拔差为5m.B卷（共20分）一、填空题（每小题4分，共12分）19. 如图，长方体的底面边长分别为1 cm和3 cm，高为6 cm.若用一根细线从点 A 开始经过4个侧面缠绕一圈到达点 B ，则所用细线最短需要 cm.10　 20. 已知一次函数 y ＝（1－3 k ） x ＋ k 的函数值 y 随着 x 值的增大而增大，且图象经过第一、二、三象限，则 k 的取值范围是 ⁠.    二、解答题（本大题满分8分）22. （1）如图，河道上 A ， B 两点（看作直线上的两点）相距200 m， C ， D 为两个菜园（看作两个点）， AD ⊥ AB ， BC ⊥ AB ，垂足分别为 A ， B ， AD ＝80 m， BC ＝70 m，现在菜农要在 AB 上确定一个抽水点 P ，使得抽水点 P 到两个菜园 C ， D 的距离和最短，求该最短距离； 17　（1）解：如图1，作点 C 关于 AB 的对称点 E ，连接 PD ， PC ， PE ， DE . 由题意，得 PC ＝ PE ， PC ＋ PD ＝ PD ＋ PE . 由三角形的三边关系，得 PD ＋ PE ＞ DE ，所以当 D ， P ， E 三点共线时， PD ＋ PE ＝ DE . 所以 PC ＋ PD 的最小值为 DE 的长度. 图1图1 图2演示完毕 谢谢观看