沪科版初中九年级数学上册专项素养巩固训练卷(二)抛物线背景下的线段、面积的最值问题练课件

这是一份沪科版初中九年级数学上册专项素养巩固训练卷(二)抛物线背景下的线段、面积的最值问题练课件，共23页。
类型一　线段的最值问题
1. (2023四川资阳中考节选,24,★★☆)如图,直线y= x+3与x轴、y轴分别交于A、B两点,抛物线y=- x2+bx+c经过A、B两点. (1)求抛物线的表达式;(2)点D是抛物线上位于第二象限内的点,过点D作x轴的平行线与直线AB交于点 C,求DC的长的最大值. 
∴C ,∴DC=-m2-3m-m=-m2-4m=-(m+2)2+4,∴当m=-2时,DC的值最大,则DC的长的最大值为4.
方法归纳　直接构造二次函数求线段最值　　当要求最值的线段平行于坐标轴时,常通过设点的坐标,表示出线段长,化简 后得到一个二次函数,利用二次函数的最值求出线段的最值.
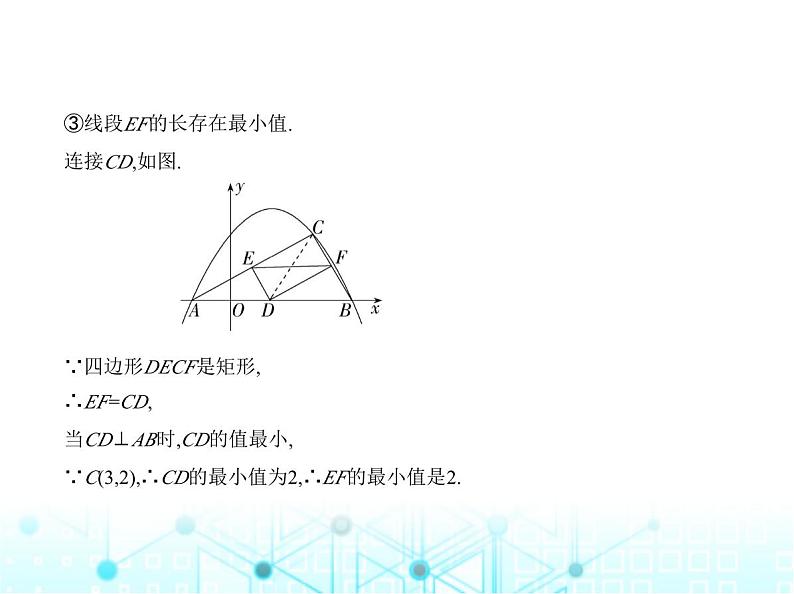
2. [最短距离问题](★★★)如图,已知抛物线y=- (x-k)2+h经过点A(-1,0),且对称轴为直线x= .     (1)求抛物线的表达式.(2)若C(m,m-1)是抛物线上位于第一象限内的点,D是线段AB上的一个动点(不与 A、B重合),过点D分别作DE∥BC交AC于E,DF∥AC交BC于F.①求点C的坐标.②求证:四边形DECF是矩形.③连接EF,线段EF的长是否存在最小值?若存在,求出EF的最小值;若不存在,请 说明理由.
③线段EF的长存在最小值.连接CD,如图. ∵四边形DECF是矩形,
∴EF=CD,当CD⊥AB时,CD的值最小,∵C(3,2),∴CD的最小值为2,∴EF的最小值是2.
类型二　线段和的最值问题
3. [将军饮马模型](2023湖南张家界中考节选,23,★★☆)如图,在平面直角坐标 系中,已知二次函数y=ax2+bx+c的图象与x轴交于点A(-2,0)和点B(6,0),与y轴交于 点C(0,6),点D为线段BC上的一动点.    (1)求二次函数的表达式;(2)如图,求△AOD周长的最小值. 
4. (2023宁夏中考,25,★★★)如图,抛物线y=ax2+bx+3(a≠ 0)与x轴交于A,B两点,与y轴交于点C.已知点A的坐标是(-1,0),抛物线的对称轴是 直线x=1.    (1)直接写出点B的坐标;(2)在对称轴上找一点P,使PA+PC的值最小,求点P的坐标和PA+PC的最小值;(3)第一象限内的抛物线上有一动点M,过点M作MN⊥x轴,垂足为N,连接BC交MN 于点Q,依题意补全图形,当MQ+ CQ的值最大时,求点M的坐标.      
解析    (1)∵抛物线y=ax2+bx+3(a≠0)的对称轴是直线x=1,∴- =1,∴b=-2a①.∵抛物线y=ax2+bx+3(a≠0)与x轴交于A,B两点,点A的坐标是(-1,0),∴a-b+3=0②.联立①②得 解得 ∴二次函数的表达式为y=-x2+2x+3,令y=0,得-x2+2x+3=0,解得x=3或x=-1,∴点B的坐标为(3,0).(2)如图1,连接BC,线段BC与直线x=1的交点即为满足条件的点P,
此时PA+PC的值最小,设直线CB的表达式为y=kx+b',把C(0,3)和B(3,0)代入,得 解得 ∴直线CB的表达式为y=-x+3,当x=1时,y=2,∴P(1,2),∵OB=OC=3,∴在Rt△BOC中,BC=3 ,∵点A,B关于直线x=1对称,∴PA=PB,
∴PA+PC=PB+PC=BC=3 . (3)补全图形如图2所示,由(1)知抛物线的表达式为y=-x2+2x+3,由(2)知yBC=-x+3,设M(t,-t2+2t+3),则Q(t,-t+3),∴MQ=-t2+3t,过点Q作QD⊥OC,垂足为D,则△CDQ是等腰直角三角形,∴CQ= t,
∴MQ+ CQ=-t2+3t+2t=-t2+5t=- + ,∴当t= 时,MQ+ CQ有最大值,此时点M的坐标为 . 
类型三　线段差的最值问题
5. (2022湖南常德中考,25,★★★)如图,已知抛物线过点O(0,0),A(5,5),且它的对称轴为直线x=2,点B是抛物线对称轴上的一点,且点B在第一象限.(1)求此抛物线的表达式;(2)当△OAB的面积为15时,求点B的坐标;(3)在(2)的条件下,P是抛物线上的动点,当PA-PB的值最大时,求点P的坐标以及 PA-PB的最大值. 
∵S△OAB=15,∴ ×|m-2|×5=15,解得m=8或m=-4(舍).∴点B的坐标为(2,8). (3)设直线AB的表达式为y=cx+d,把A(5,5),B(2,8)代入,得 解得 
∴直线AB的表达式为y=-x+10,如图2,当PA-PB的值最大时,A、B、P在同一条直线上(点P不与点A重合),∵P是抛物线上的动点,∴当PA-PB的值最大时,点P为直线AB与抛物线的另一个交点,∴ 解得 或 (舍去),∴P(-2,12),此时PA-PB=AB= =3 .
类型四　面积的最值问题
6. (2024安徽淮北月考,23,★★★)已知抛物线与x轴相交 于A,B两点,与y轴相交于点C(0,6),顶点为D(2,8).    (1)求此抛物线的表达式;(2)如图①,点P为抛物线对称轴(直线l)上的动点,求当|PB-PC|取得最小值时点P 的坐标;(3)如图②,在第一象限内,抛物线上有一动点M,求△BCM面积的最大值.      
解析    (1)∵抛物线的顶点为D(2,8),∴可设其表达式为y=a(x-2)2+8,代入点C(0,6),得a(0-2)2+8=6,解得a=- ,∴抛物线的表达式为y=- (x-2)2+8.(2)当y=0时,- (x-2)2+8=0,解得x1=-2,x2=6,∴A(-2,0),B(6,0),∵点P为抛物线对称轴上的动点,∴可设P(2,m),∴当PB=PC时,|PB-PC|取得最小值,为0,