沪科版初中九年级数学上册专项素养巩固训练卷(五)证比例式或等积式的技巧练课件

这是一份沪科版初中九年级数学上册专项素养巩固训练卷(五)证比例式或等积式的技巧练课件，共21页。
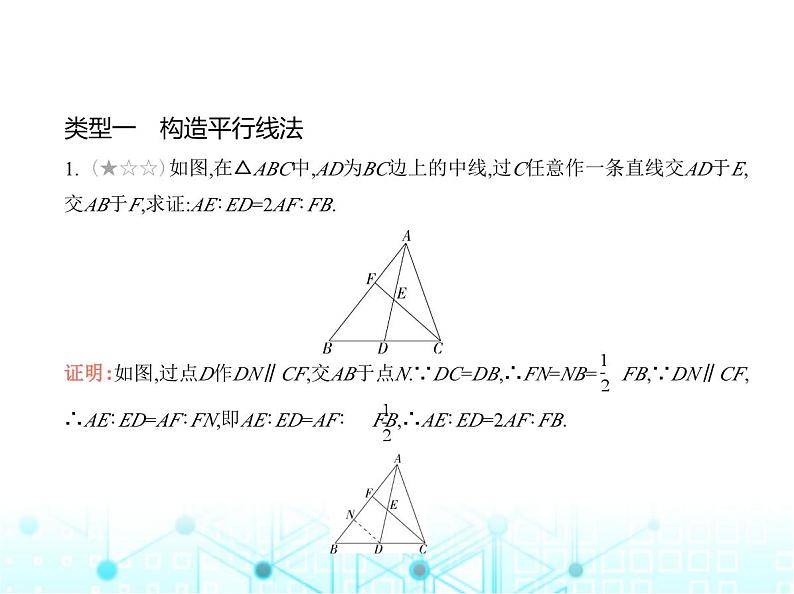
1. (★☆☆)如图,在△ABC中,AD为BC边上的中线,过C任意作一条直线交AD于E, 交AB于F,求证:AE∶ED=2AF∶FB. 证明:如图,过点D作DN∥CF,交AB于点N.∵DC=DB,∴FN=NB= FB,∵DN∥CF,∴AE∶ED=AF∶FN,即AE∶ED=AF∶ FB,∴AE∶ED=2AF∶FB. 
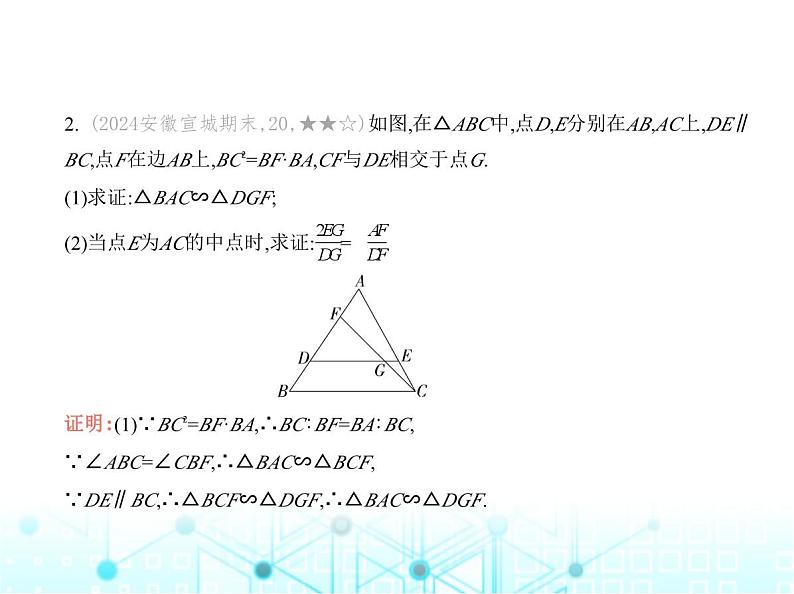
2. (2024安徽宣城期末,20,★★☆)如图,在△ABC中,点D,E分别在AB,AC上,DE∥ BC,点F在边AB上,BC2=BF·BA,CF与DE相交于点G.    (1)求证:△BAC∽△DGF;(2)当点E为AC的中点时,求证: = . 证明:(1)∵BC2=BF·BA,∴BC∶BF=BA∶BC,∵∠ABC=∠CBF,∴△BAC∽△BCF,∵DE∥BC,∴△BCF∽△DGF,∴△BAC∽△DGF.
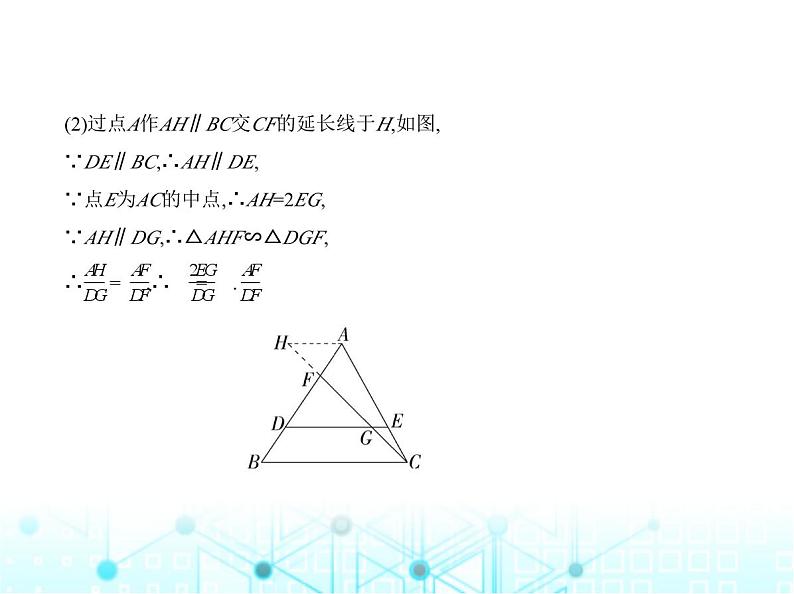
(2)过点A作AH∥BC交CF的延长线于H,如图,∵DE∥BC,∴AH∥DE,∵点E为AC的中点,∴AH=2EG,∵AH∥DG,∴△AHF∽△DGF,∴ = ,∴ = . 
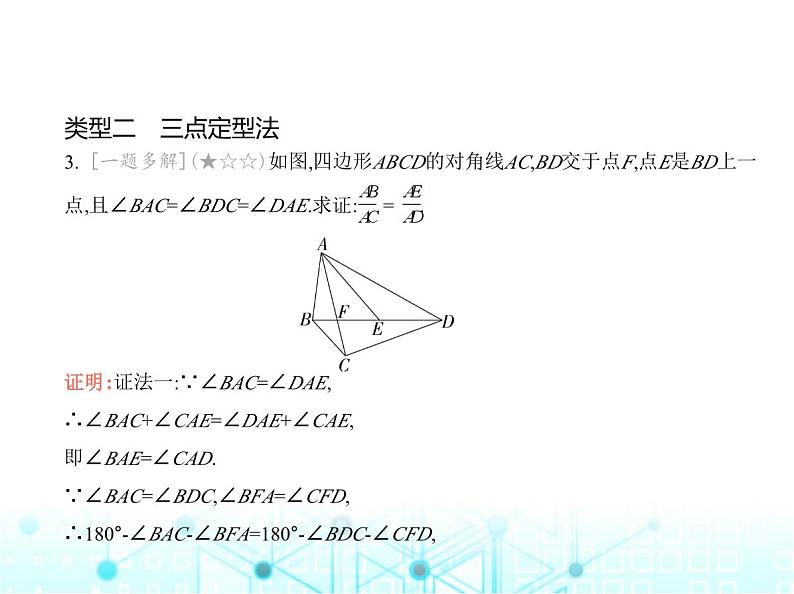
3. [一题多解](★☆☆)如图,四边形ABCD的对角线AC,BD交于点F,点E是BD上一 点,且∠BAC=∠BDC=∠DAE.求证: = . 证明:证法一:∵∠BAC=∠DAE,∴∠BAC+∠CAE=∠DAE+∠CAE,即∠BAE=∠CAD.∵∠BAC=∠BDC,∠BFA=∠CFD,∴180°-∠BAC-∠BFA=180°-∠BDC-∠CFD,
即∠ABE=∠ACD,∴△ABE∽△ACD,∴ = .证法二:∵∠BAC=∠DAE,∴∠BAC+∠CAE=∠DAE+∠CAE,即∠BAE=∠CAD.又∵∠BEA=∠DAE+∠ADE,∠ADC=∠BDC+∠ADE,∠DAE=∠BDC,∴∠AEB=∠ADC.∴△ABE∽△ACD,∴ = .
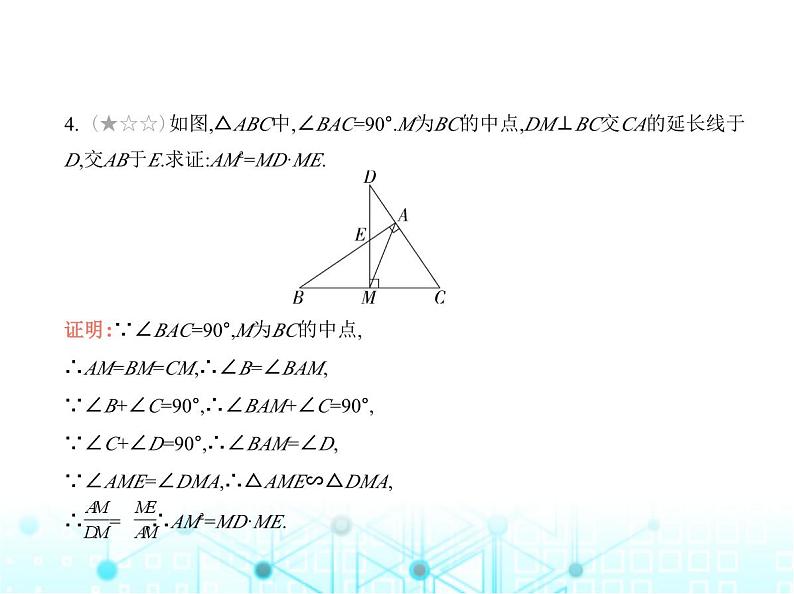
4. (★☆☆)如图,△ABC中,∠BAC=90°.M为BC的中点,DM⊥BC交CA的延长线于 D,交AB于E.求证:AM2=MD·ME. 证明:∵∠BAC=90°,M为BC的中点,∴AM=BM=CM,∴∠B=∠BAM,∵∠B+∠C=90°,∴∠BAM+∠C=90°,∵∠C+∠D=90°,∴∠BAM=∠D,∵∠AME=∠DMA,∴△AME∽△DMA,
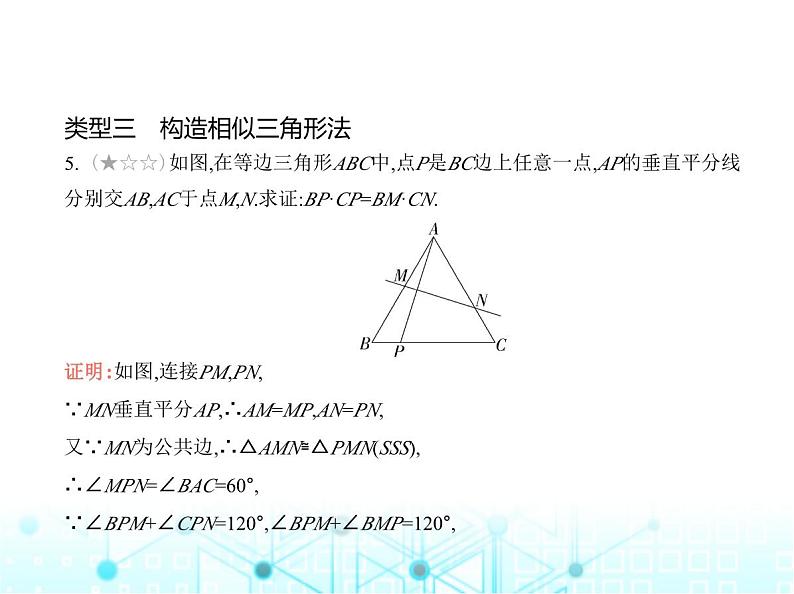
类型三　构造相似三角形法
5. (★☆☆)如图,在等边三角形ABC中,点P是BC边上任意一点,AP的垂直平分线 分别交AB,AC于点M,N.求证:BP·CP=BM·CN. 证明:如图,连接PM,PN,∵MN垂直平分AP,∴AM=MP,AN=PN,又∵MN为公共边,∴△AMN≌△PMN(SSS),∴∠MPN=∠BAC=60°,∵∠BPM+∠CPN=120°,∠BPM+∠BMP=120°,
∴∠BMP=∠CPN,又∵∠B=∠C=60°,∴△MPB∽△PNC,∴ = ,即BP·CP=BM·NC.  
6. (新独家原创,★★☆)如图,F为正方形ABCD的边AB的中点,E是AD上的一点, AE= AD,FG⊥CE于G.求证:FG2=EG·CG.     证明:如图,连接EF,CF.∵AE= AD,AF=BF= AB,四边形ABCD为正方形,∴ = = ,∵∠A=∠B=90°,∴△EFA∽△FCB,∴∠AFE=∠BCF.∵∠BFC+∠BCF=90°,∴∠AFE+∠BFC=90°,∴∠EFC=90°,∴∠EFG+∠CFG=90°.
又∵FG⊥CE,∴∠EFG+∠FEG=90°,∴∠CFG=∠FEG.∵∠EGF=∠CGF=90°,∴△EFG∽△FCG,∴ = ,∴FG2=EG·CG. 
类型四　等比或等积代换法
7. (2024安徽滁州定远期末,19,★☆☆)如图,点E为▱ABCD的边CD延长线上的 一点,连接BE交AC于点O,交AD于点F.(1)求证: = ;(2)求证:BO2=EO·FO. 
8. (★☆☆)如图,在△ABC中,AB=AC,DE∥BC,点F在边AC上,DF与BE相交于点G, 且∠EDF=∠ABE.求证:    (1)△DEF∽△BDE;(2)△GDE∽△EDF;(3)DG·DF=DB·EF. 证明:(1)∵AB=AC,∴∠ABC=∠ACB,∵DE∥BC,∴∠ABC+∠BDE=180°,∠ACB+∠CED=180°.∴∠BDE=∠CED,
∵∠EDF=∠ABE,∴△DEF∽△BDE.(2)∵△DEF∽△BDE,∴∠BED=∠DFE.∵∠GDE=∠EDF,∴△GDE∽△EDF.(3)由(2)知,△GDE∽△EDF,∴ = ,∴DE2=DG·DF,∵△DEF∽△BDE,∴ = ,∴DE2=DB·EF,∴DG·DF=DB·EF.
9. (★☆☆)如图,D是△ABC的边AB上一点,DE∥BC,交边AC于点E,延长DE至点 F,使EF=DE,连接BF,交边AC于点G,连接CF.(1)求证: = ;(2)如果CF2=FG·FB,求证:CG·CE=BC·DE. 证明:(1)∵DE∥BC,∴△ADE∽△ABC,△EFG∽△CBG,∴ = , = ,又∵DE=EF,∴ = ,∴ = .
(2)∵CF2=FG·FB,∴ = ,又∵∠CFG=∠CFB,∴△CFG∽△BFC,∴ = ,∠FCE=∠CBF,又∵DF∥BC,∴∠EFG=∠CBF,∴∠FCE=∠EFG,又∵∠ FEG=∠CEF,∴△EFG∽△ECF,∴ = = ,∴ = ,即CG·CE=BC·DE.
10. (2024安徽合肥庐阳期末,21,★★☆)如图,在△ABC中,点D,E分别在边AB,AC 上,ED、CB的延长线相交于点F.(1)如图①,若∠FBD=∠FEC,BF=4,FD=5,FE=8,求FC的长;(2)如图②,若BD=CE,求证: = .      解析    (1)∵∠FBD=∠FEC,∠BFD=∠EFC,∴△FBD∽△FEC,∴FB∶FE=FD∶ FC,即4∶8=5∶FC,解得FC=10.(2)证明:过点D作DM∥AC交FC于点M,如图,∵DM∥AC,∴△BDM∽△BAC,
∴  = ,∴ = ,∵BD=CE,∴ = .∵DM∥CE,∴△FCE∽△FMD,∴ = ,∴ = . 
11. (2024安徽六安裕安中学月考,19,★☆☆)如图,直线DN平行于△ABC的中线 AF交AB于点D,交CA的延长线于点E,交BC于点N,求证: = . 证明:由DN∥AF易得 = , = ,∵在△ABC中,AF是BC边上的中线,∴ FB=FC,∴ = .