沪科版初中九年级数学上册专项素养巩固训练卷(六)相似三角形的基本类型练课件

这是一份沪科版初中九年级数学上册专项素养巩固训练卷(六)相似三角形的基本类型练课件，共22页。
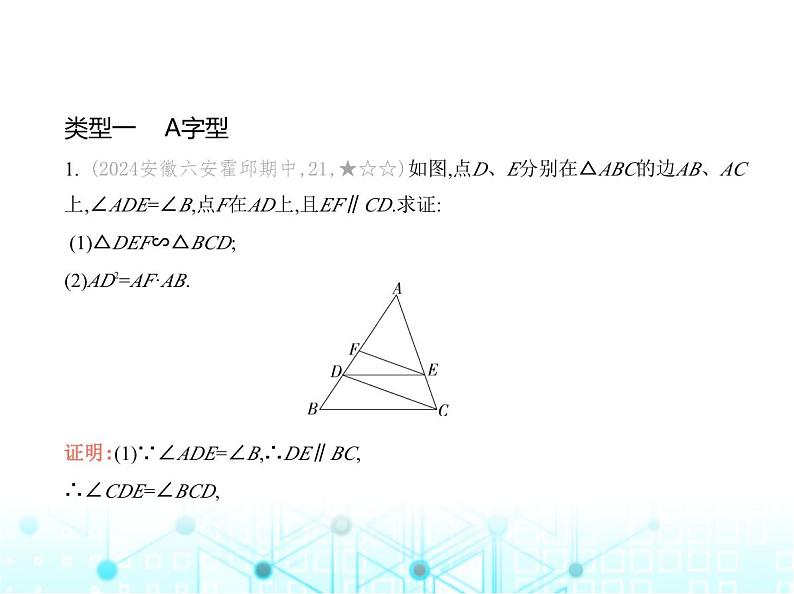
类型一    A字型1. (2024安徽六安霍邱期中,21,★☆☆)如图,点D、E分别在△ABC的边AB、AC 上,∠ADE=∠B,点F在AD上,且EF∥CD.求证:     (1)△DEF∽△BCD;(2)AD2=AF·AB. 证明:(1)∵∠ADE=∠B,∴DE∥BC,∴∠CDE=∠BCD,
∵EF∥CD,∴∠CDE=∠DEF,∴∠BCD=∠DEF,∵∠ADE=∠B,∴△DEF∽△BCD.(2)∵∠ADE=∠B,∴DE∥BC,∴∠AED=∠ACB,∴△ADE∽△ABC,∴ = ,∵EF∥CD,∴∠AEF=∠ACD,∴△AEF∽△ACD,∴ = ,∴ = ,∴AD2=AF·AB.
2. (2024安徽阜阳太和期末,18,★☆☆)如图,△ABC中,∠A=55°,∠B=45°,点D、E 分别在△ABC的边AB、AC上,且∠ADE=80°.(1)求证:△AED∽△ABC;(2)如果AD=4,BD=6,AE=5,求CE的长. 解析    (1)证明:∵∠A=55°,∠B=45°,∴∠C=80°, ∵∠A=∠A,∠ADE=∠C,∴△AED∽△ABC.
(2)由(1)得△AED∽△ABC,∴ = ,∵AD=4,BD=6,∴AB=10,∵AE=5,∴ = ,∴AC=8,∴CE=AC-AE=8-5=3.
类型二    X(8)字型
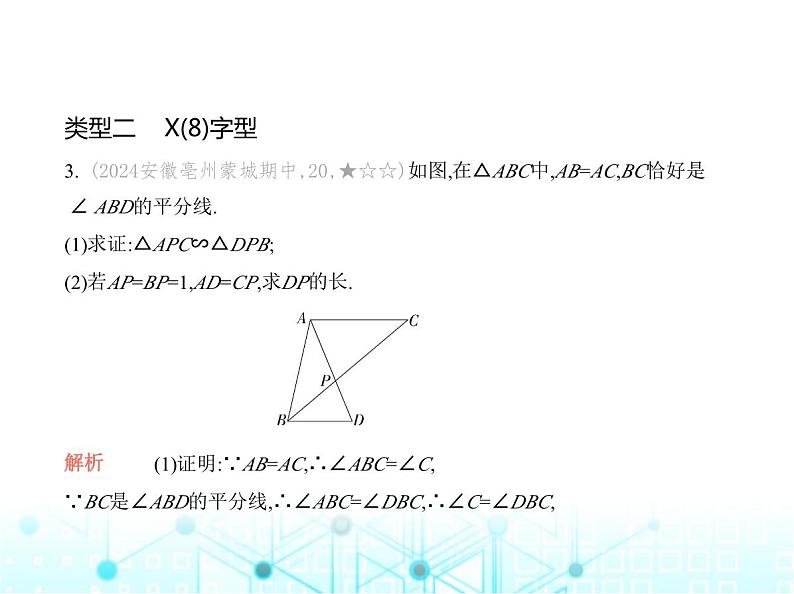
3. (2024安徽亳州蒙城期中,20,★☆☆)如图,在△ABC中,AB=AC,BC恰好是 ∠ ABD的平分线.    (1)求证:△APC∽△DPB;(2)若AP=BP=1,AD=CP,求DP的长. 解析    (1)证明:∵AB=AC,∴∠ABC=∠C,∵BC是∠ABD的平分线,∴∠ABC=∠DBC,∴∠C=∠DBC,
又∵∠APC=∠DPB,∴△APC∽△DPB.(2)设DP=x,∵AP=PB=1,∴AD=AP+DP=1+x,∵AD=CP,∴CP=1+x,由(1)得△APC∽△DPB,∴AP∶DP=PC∶BP,即1∶x=(x+1)∶1,∴x2+x=1,∴x2+x-1=0,解得x1= ,x2= (不合题意,舍去).∴DP= .
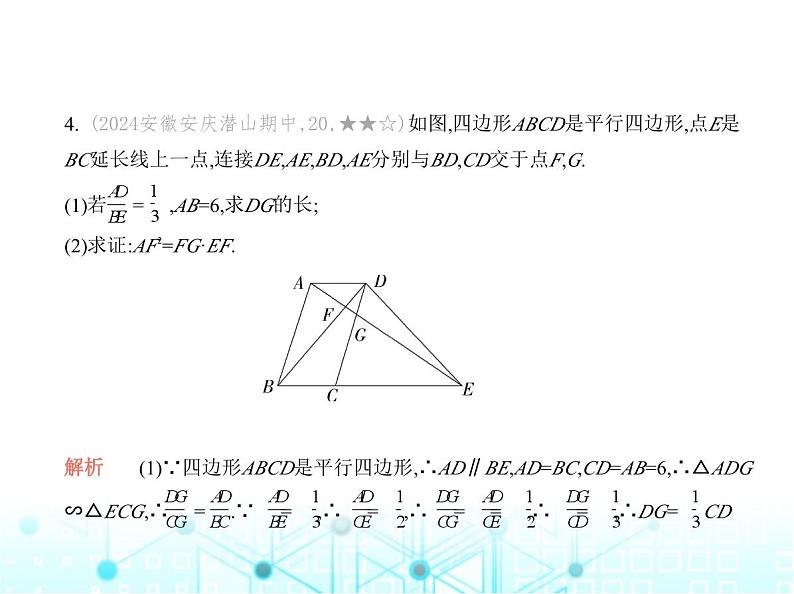
4. (2024安徽安庆潜山期中,20,★★☆)如图,四边形ABCD是平行四边形,点E是 BC延长线上一点,连接DE,AE,BD,AE分别与BD,CD交于点F,G.(1)若 = ,AB=6,求DG的长;(2)求证:AF2=FG·EF. 解析    (1)∵四边形ABCD是平行四边形,∴AD∥BE,AD=BC,CD=AB=6,∴△ADG ∽△ECG,∴ = .∵ = ,∴ = ,∴ = = ,∴ = ,∴DG= CD
= ×6=2.(2)证明:∵四边形ABCD是平行四边形,∴AD∥BE,AB∥CD,∴△DFG∽△BFA, △ADF∽△EBF,∴ = , = ,∴ = ,即AF2=FG·EF.
5. [分类讨论思想](★★☆)如图,AD∥BC,AB⊥BC于点B,AB=8,AD=3,BC=4,点P 为AB边上一动点,若△PAD与△PBC是相似三角形,求AP的长.解析　∵AB⊥BC,∴∠B=90°.∵AD∥BC,∴∠A=180°-∠B=90°,∴∠PAD= ∠PBC=90°.设AP的长为x,则BP的长为8-x.若AB边上存在点P,使△PAD与△PBC 相似,则分以下两种情况:①若△APD∽△BPC,则AP∶BP=AD∶BC,即x∶(8-x)= 3∶4,解得x= ;②若△APD∽△BCP,则AP∶BC=AD∶BP,即x∶4=3∶(8-x),解得x=2或x=6.故AP的长为 或2或6.
6. (★☆☆)如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+ ∠CBE=90°,连接BF.    (1)求证:△CAE∽△CBF;(2)若BE=1,AE=2,求CE的长. 解析    (1)证明:∵△ABC和△CEF均为等腰直角三角形,∴ = = ,∠ACB=∠ECF=45°,∴∠ACE=∠BCF,∴△CAE∽△CBF.
(2)∵△CAE∽△CBF,∴∠CAE=∠CBF, = = ,∵AE=2,∴ = ,∴BF= ,∵∠CAE+∠CBE=90°,∴∠CBF+∠CBE=90°,∴∠EBF=90°,∴EF2=BE2+BF2=12+( )2=3,∴EF= ,∵ CE2=2EF2=6,∴CE= .
7. (2024江苏扬州梅苑双语学校,23,★☆☆)如图,∠BAD=∠CAE,∠ABD=∠ACE. 求证:(1)AB·AE=AC·AD;(2)△ABC∽△ADE. 证明:(1)∵∠BAD=∠CAE,∠ABD=∠ACE,∴△ABD∽△ACE,∴ = ,∴AB·AE=AC·AD.
(2)∵∠BAD=∠CAE,∴∠BAD+∠DAC=∠DAC+∠CAE,即∠BAC=∠DAE,∵ = ,∴ = ,∴△ABC∽△ADE.
8. (★☆☆)如图,在△ABC中,D为BC上一点,AD平分∠BAC,AD=DC.(1)求证:△ABC∽△DBA;(2)若BD=2,DC=3,求AC的长.解析    (1)证明:∵AD平分∠BAC,∴∠BAD=∠CAD,∵AD=DC,∴∠CAD=∠C,∴∠BAD=∠C.∵∠B=∠B,∴△ABC∽△DBA.(2)∵BD=2,DC=3,∴BC=5,∵AD=DC,∴AD=3.
9. (2023黑龙江绥化期末,12,★☆☆)如图,AD,BC是△AOB的两条高,AD=2OD,连 接CD,下列结论:①BC=2OC;②△AOB∽△DOC;③ = .其中正确的个数为 (　    ) A.0　　　    B.1　　　    C.2　　　    D.3
10. (★☆☆)如图,AD为直角三角形ABC斜边上的高,DE⊥AB于点E,图中相似三 角形共有　　　    对. 
答案    10解析　∵AD是Rt△ABC斜边上的高,DE⊥AB,∴∠AED=∠ADC=∠BED=∠ADB =∠CAB=90°.∵∠C=∠C,∠B=∠B,∴△ACD∽△BCA∽△BDE∽△BAD,∵∠DAE=∠BAD,∴△DAE∽△BAD,∴△ACD∽△BCA∽△BDE∽△BAD∽△DAE,∴题图中共有10对相似三角形.
11. (2023湖南邵阳中考,21,★☆☆)如图,CA⊥AD,ED⊥AD,点B是线段AD上的一 点,且CB⊥BE.已知AB=8,AC=6,DE=4.    (1)证明:△ABC∽△DEB;(2)求线段BD的长.解析    (1)证明:∵CA⊥AD,ED⊥AD,CB⊥BE,∴∠A=∠CBE=∠D=90°,∴∠C+ ∠CBA=90°,∠CBA+∠DBE=90°,∴∠C=∠DBE,∴△ABC∽△DEB.(2)∵△ABC∽△DEB,∴ = ,∴ = ,∴BD=3.
12. (★☆☆)如图,在等边△ABC中,边长为6,D是BC边上的动点,∠EDF=60°.(1)求证:△BDE∽△CFD;(2)当BD=1,CF=3时,求BE的长. 解析    (1)证明:∵△ABC为等边三角形,∴∠B=∠C=60°,∵∠EDF=60°,∴∠BED +∠EDB=∠EDB+∠FDC=120°,∴∠BED=∠FDC,∴△BDE∽△CFD.(2)由(1)知△BDE∽△CFD,∴ = ,∵BC=6,BD=1,∴CD=BC-BD=5,∴ = ,解得BE= .
13. (2024安徽合肥月考,21,★★☆)如图,在△ABC中,AB=AC,中线AE与高CD相 交于点P,连接DE.    (1)求证:PA·PE=PC·PD;(2)过点E作EF⊥AC于点F,求 的值.