沪科版初中九年级数学上册专项素养巩固训练卷(八)阅读理解试题练课件

这是一份沪科版初中九年级数学上册专项素养巩固训练卷(八)阅读理解试题练课件，共8页。
类型一　二次函数中的阅读理解试题
1. (2023安徽滁州二模,22,★★☆)【阅读理解】已知关于x的二次函数y=x2-2ax+ a2+2a=(x-a)2+2a,它的图象的顶点坐标为(a,2a),故无论a取何值时,对应的抛物线的顶点都在直线y=2x上,我们称顶点位于同一条直线上且形状相同的抛物线所对应的函数为同源二次函数,该条直线所对应的函数为根函数.  【问题解决】(1)若二次函数y=x2+2x-3和y=-x2-4x-3是同源二次函数,求它们的根函数.(2)已知关于x的二次函数C:y=x2-4mx+4m2-4m+1,完成下列问题:①求满足二次函数C的所有二次函数的根函数;②若二次函数C的图象与直线x=-3交于点P,求点P到x轴的最小距离及此时m的值.
解析    (1)∵y=x2+2x-3=(x+1)2-4,∴该抛物线的顶点坐标为(-1,-4).∵y=-x2-4x-3=-(x +2)2+1,∴该抛物线的顶点坐标为(-2,1).设经过点(-1,-4)和点(-2,1)的直线的表达 式为y=kx+b,∴ 解得 ∴y=-5x-9,∴它们的根函数为y=-5x-9.(2)①∵y=x2-4mx+4m2-4m+1=(x-2m)2-4m+1,∴该抛物线的顶点坐标为(2m,-4m+1), 设顶点(2m,-4m+1)在直线y=ax+1上,∴-4m+1=2ma+1,解得a=-2,∴顶点(2m,-4m+1) 在直线y=-2x+1上,∴满足二次函数C的所有二次函数的根函数为y=-2x+1.②∵二次函数C的图象与直线x=-3交于点P,∴当x=-3时,y=(-3)2-4m×(-3)+4m2-4m+ 1=4m2+8m+10.∴P(-3,4m2+8m+10).∵4m2+8m+10=4(m+1)2+6,∴当m=-1时,点P的 纵坐标的最小值为6.∴点P到x轴的最小距离为6,此时m=-1.
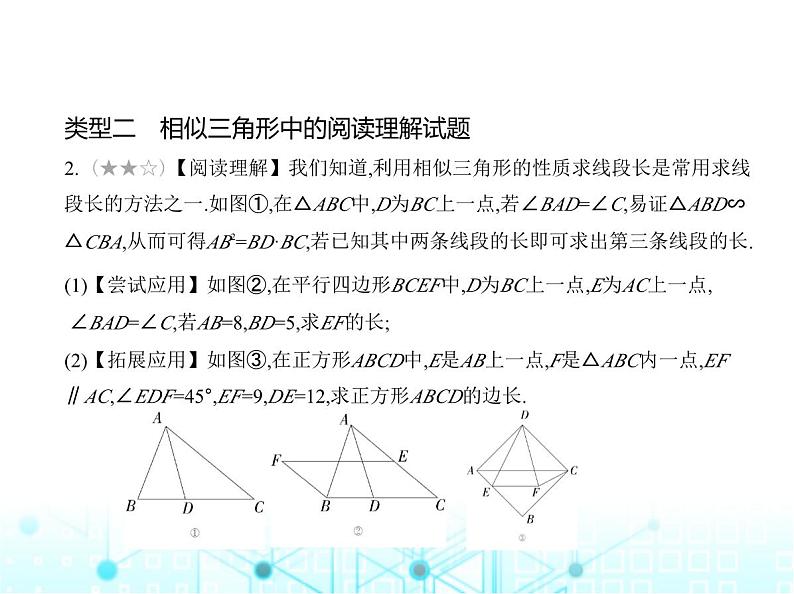
类型二　相似三角形中的阅读理解试题
2. (★★☆)【阅读理解】我们知道,利用相似三角形的性质求线段长是常用求线 段长的方法之一.如图①,在△ABC中,D为BC上一点,若∠BAD=∠C,易证△ABD∽△CBA,从而可得AB2=BD·BC,若已知其中两条线段的长即可求出第三条线段的长.(1)【尝试应用】如图②,在平行四边形BCEF中,D为BC上一点,E为AC上一点, ∠BAD=∠C,若AB=8,BD=5,求EF的长;(2)【拓展应用】如图③,在正方形ABCD中,E是AB上一点,F是△ABC内一点,EF ∥AC,∠EDF=45°,EF=9,DE=12,求正方形ABCD的边长.
解析    (1)∵∠BAD=∠C,∠ABD=∠CBA,∴△ABD∽△CBA,∴ = ,即 = ,解得BC= ,∵四边形BCEF为平行四边形,∴EF=BC= .(2)如图,分别延长EF,DC相交于点G.
∵四边形ABCD是正方形,∴∠ACD=45°,AC= AD,∵EF∥AC,∴∠EGD=∠ACD=45°,∵∠EDF=45°,∴∠EDF=∠EGD,∵∠DEG=∠DEF,∴△EDF∽△EGD,∴ = ,即 = ,解得EG=16,∵AC∥EG,AB∥CD,∴四边形AEGC为平行四边形,∴AC=EG=16,∴AD= ×16=8 .
类型三　三角函数中的阅读理解试题
3. (2024黑龙江哈尔滨期中,25,★★☆)阅读理解:通过学习三角函数,我们知道在 直角三角形中,一个锐角的大小,与两条边长的比值相互唯一确定,因此边长与角 的大小之间可以相互转化.类似地,可以在等腰三角形中,建立边角之间的联系. 我们定义:等腰三角形中底边与腰的比叫做顶角正对(sad).如图①,在△ABC中, AB=AC,顶角A的正对记作sad A,这时sad A=底边÷腰= .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述顶角正对的定义,解下列问题.(1)计算sad 60°=　　    ;(2)对于0°