沪科版初中九年级数学上册专项素养综合练(六)函数与相似综合题课件

这是一份沪科版初中九年级数学上册专项素养综合练(六)函数与相似综合题课件，共13页。
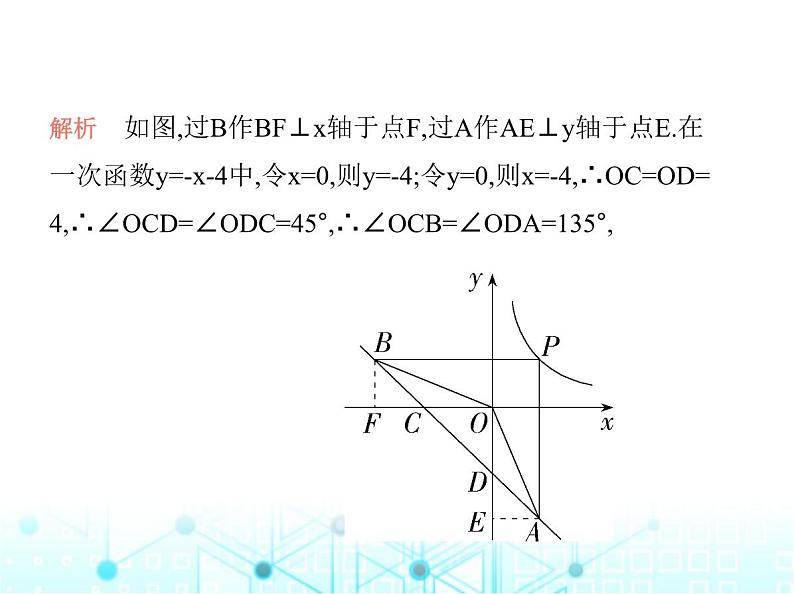
类型一　反比例函数与相似结合1.(2024安徽安庆潜山期中)如图,直线y=-x-4分别交x轴、y轴 于点C,D,点P为反比例函数y= (k>0)在第一象限内的图象上的一点,过点P分别作x轴、y轴的垂线交直线CD于点A,B,且 ∠AOB=135°,则下列结论错误的是 (　    )A.△AOD与△OBC相似B.BP=APC.BC·AD=16D.k=9
解析　如图,过B作BF⊥x轴于点F,过A作AE⊥y轴于点E.在 一次函数y=-x-4中,令x=0,则y=-4;令y=0,则x=-4,∴OC=OD= 4,∴∠OCD=∠ODC=45°,∴∠OCB=∠ODA=135°,
∠BCF=∠ADE=45°,∴△COD,△BFC和△ADE都是等腰直 角三角形,∴BC= BF,AD= AE.∵∠AOB=135°,∴∠OBC+∠BAO=45°.又∵∠OBC+∠BOC=45°,∴∠BAO=∠BOC, ∴△AOD∽△OBC,故选项A正确,不符合题意;∵△BFC和△ ADE都是等腰直角三角形,∴∠CBF=∠DAE=45°,∴∠PBC= ∠PAB=45°,∴BP=AP,故选项B正确,不符合题意;∵△AOD ∽△OBC,∴ = ,即AD·BC=OC·OD=16,故选项C正确,不符合题意;设P(m,n),则k=mn,BC= BF= n,AD= AE= m,∴ m× n=16,即mn=8=k,故选项D错误,符合题意.
2.(2023江苏镇江中考)如图,正比例函数y=-3x与反比例函数y = (k≠0)的图象交于A、B(1,m)两点,C点在x轴负半轴上,∠ACO=45°.(1)m=　    ,k=　    ,点C的坐标为　　　    ;(2)点P在x轴上,若以B、O、P为顶点的三角形与△AOC相 似,求点P的坐标.
解析    (1)当x=1时,y=-3x=-3=m,即点B(1,-3),将点B的坐标代 入反比例函数的表达式,得k=-3×1=-3,即反比例函数的表达式为y=- ,联立得 解得 或 ∴点A(-1,3),
如图,过点A作AH⊥x轴于点H,∵A点坐标为(-1,3),∴AH=3, OH=1,∵∠ACO=45°,∴CH=AH=3,则CO=CH+OH=4,则点C 的坐标为(-4,0).(2)当点P在x轴的负半轴上时,∵∠BOP>90°>∠AOC,∠BOP>∠ACO,∠BOP>∠CAO,∴△BOP和△AOC不可能相似;当点P在x轴的正半轴上时,∠AOC=∠BOP,若△AOC∽△BOP,则 = =1,
则OP=OC=4,即点P(4,0);若△AOC∽△POB,则 = ,由(1)知AO= = ,同理可得OB= ,即 = ,解得OP=2.5,即点P(2.5,0).综上,点P的坐标为(4,0)或(2.5,0).
类型二　二次函数与相似结合3.(新考向·新定义试题)给出定义:抛物线y=ax2+bx+c(a≠0)与 x轴交于A,B两点,与y轴交于点C,连接AC、CB,若满足△A- CO∽△CBO,则称这样的抛物线为“相似抛物线”,如图,二 次函数y=ax2+bx+2(a≠0)的图象是“相似抛物线”,且AC=2  ,则此抛物线的对称轴为　　　　　    .
解析　在y=ax2+bx+2中,令x=0,则y=2,∴C(0,2),∴OC=2.∵△ ACO∽△CBO,AC=2 ,∴ = = ,即 = = ,设OB=x,则BC= x,∵∠BOC=90°,∴OB2+OC2=BC2,即x2+22=( x)2,∴x=1,∴OB=1,∴B(1,0),OA= =4,∴A(-4,0),∴此抛物线的对称轴为直线x= =-1.5.
4.(2024陕西西安临潼期末)如图,二次函数y=ax2+bx+c(a