初中数学沪科版九年级上册21.5 反比例函数教课ppt课件

展开

这是一份初中数学沪科版九年级上册21.5 反比例函数教课ppt课件，共40页。

1.(2023安徽蚌埠禹会二模)反比例函数y=- 的大致图象是(M9121006)(　    ) A     B     C     D
解析　∵k=-1<0,∴此函数图象在第二、四象限.故选D.
2.(跨学科·物理)(2023湖南怀化中考)已知压力F(N)、压强p (Pa)与受力面积S(m2)之间有如下关系式:F=pS.当F为定值时, 下列图象大致表示压强p与受力面积S之间的函数关系的是 (M9121006)(　    ) A     B     C     D
解析　∵压力F(N)、压强p(Pa)与受力面积S(m2)之间有如下关系式:F=pS,∴当F为定值时,压强p与受力面积S之间的函数关系是反比例函数关系,故选D.
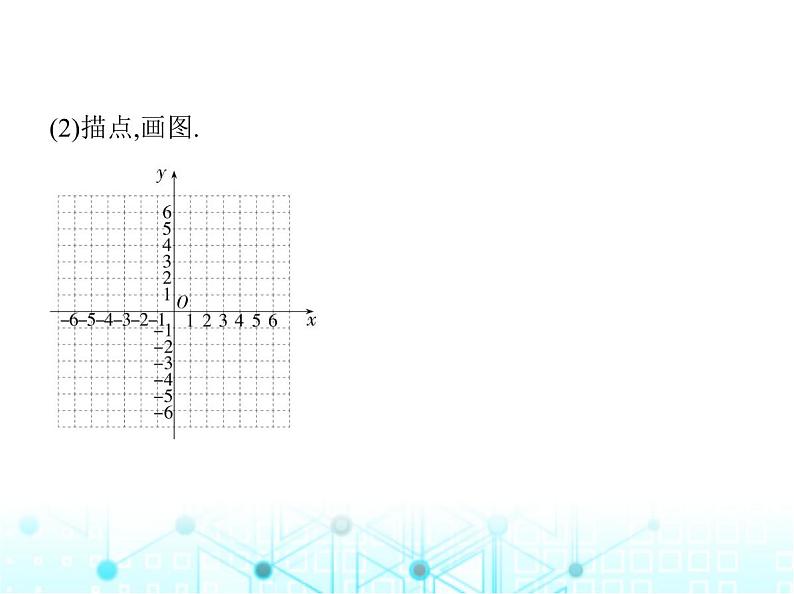
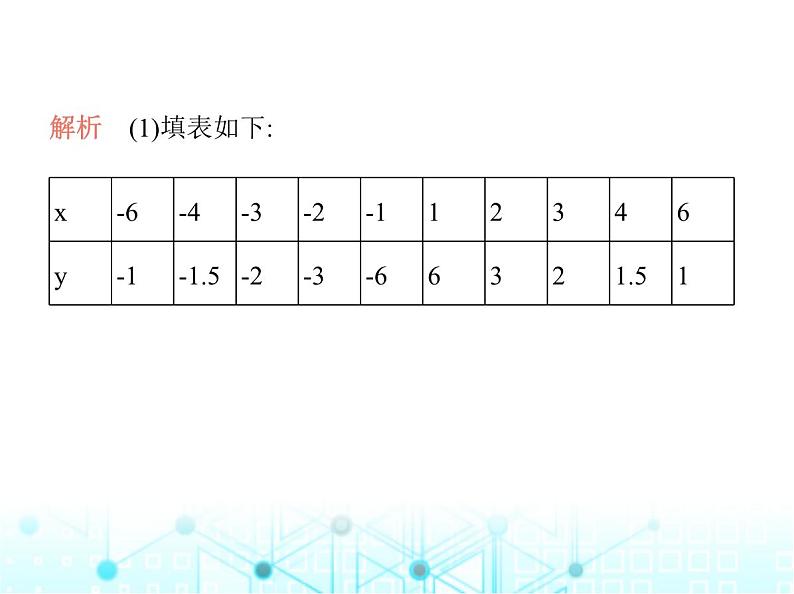
3.画出函数y= 的图象.(M9121006)(1)完成下列表格:
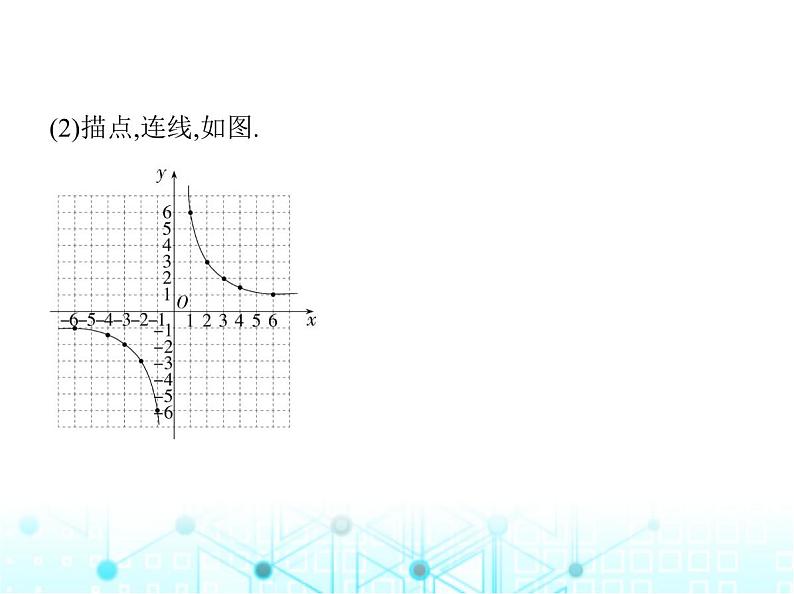
(2)描点,画图.
解析    (1)填表如下:
(2)描点,连线,如图.
5.(2024安徽合肥三十八中期中)如图,一次函数y=ax+b的图象与反比例函数y= 的图象交于点A(2,3),B(m,-2),则不等式ax+b> 的解集是(M9121006)(　    ) A.-32B.x<-3或0C.-22D.-33
6.(2023湖北武汉中考)关于反比例函数y= ,下列结论正确的是(M9121006)(　    )A.图象位于第二、四象限B.图象与坐标轴有公共点C.图象所在的每一个象限内,y随x的增大而减小D.图象经过点(a,a+2),则a=1
解析　反比例函数y= 的图象位于第一、三象限,与坐标轴没有交点,故A,B选项错误;反比例函数y= 的图象在每一个象限内,y随x的增大而减小,故C选项正确;反比例函数y= 的图象经过点(a,a+2),∴a(a+2)=3,解得a=1或a=-3,故D选项错误. 故选C.
7.(新考向·开放性试题)(2022福建中考)已知反比例函数y= 的图象分别位于第二、四象限,则实数k的值可以是　　         .(只需写出一个符合条件的实数)
解析　∵反比例函数的图象位于第二、四象限,∴k<0,∴k的取值不唯一,可取-3.答案不唯一.
(新独家原创)(转化法求面积)如图,在平面直角坐标系中,平行四边形的中心在原点,且平行四边形的一组对边与x轴平行,平行四边形的面积为4,则平行四边形与双曲线相交形成的阴影部分的面积为　　　    .(M9121006)
解析　如图,根据图象的性质,将题图中第三象限内的阴影部分与第一象限内的阴影部分拼在一起,组成的四边形OABC 的面积是平行四边形面积的 ,即所求面积为4× =1.
9.(教材变式·P47例3)已知反比例函数y= .(M9121006)(1)如果这个反比例函数的图象与直线y=- x的一个交点坐标为(a,5),求出a和k的值,并直接写出另一个交点的坐标;(2)如果对于反比例函数y= ,当x<0时,y的值随x值的增大而增大,求k的取值范围.
解析    (1)∵点(a,5)在直线y=- x上,∴5=- a,解得a=-3,∴点(-3,5)在反比例函数y= 的图象上,则5= ,解得k=-7.∵直线y=- x过原点,∴反比例函数y= 的图象与直线y=- x的另一个交点的坐标为(3,-5).
(2)由x<0时,y的值随x值的增大而增大,可知2k-1<0,解得k< .
10.(数形结合思想)(2023山东淄博临淄期末)下面四个图中反比例函数的表达式均为y= ,则阴影部分的面积为3的有 (　    ) A.1个 B.2个 C.3个 D.4个
解析　第1个题图中,阴影部分的面积为3;第2个题图中,阴影部分的面积为 ×3=1.5;第3个题图中,阴影部分的面积为2× ×3=3;第4个题图中,阴影部分的面积为3+2× ×3=6.故选B.
11.(2023云南昆明十中开学测试)如图,点A、B是双曲线y= 上的点,分别过点A、B作x轴和y轴的垂线段,若图中阴影部分的面积为2,则两个空白矩形面积的和为　　　    .(M9121 006)
解析　如图,∵点A、B是双曲线y= 上的点,∴ = =6.∵ =2,∴ + =6+6-2-2=8.
方法归纳　双曲线中的面积与k的关系如图,过双曲线y= (k≠0)上任意一点P(x,y)分别作x轴,y轴的垂线PM,PN,垂足分别为M,N,所得的矩形PMON的面积等于| k|.连接点P与原点O,还可以得到两个直角三角形,这两个直角三角形的面积都等于 .k的正负性可由图象所在象限确定.
解析如图,连接正方形的对角线,由正方形的性质知对角线交于原点O,过点A,B分别作x轴的垂线,垂足分别为点C、D,点B在函数y= 的图象上,∵四边形是正方形,∴AO=BO,∠AOB=∠BDO=∠ACO=90°,∴∠CAO=90°-∠AOC=∠BOD, ∴△AOC≌△OBD,∴ = = = ,∵点A在第二象限内,∴n=-3,故选A.
13.(安徽常考·反比例函数与一次函数综合题)(2024安徽安庆期中,21, )如图,一次函数y=ax+b的图象与反比例函数y= 的图象交于A(2,m)、B(-1,-6)两点.(M9121006)(1)求反比例函数和一次函数的表达式;(2)求△AOB的面积;(3)根据图象直接写出当x为何值时,ax+b- >0.
解析    (1)把(-1,-6)代入y= ,得-6= ,解得k=6,∴反比例函数的表达式为y= .把(2,m)代入y= ,得m=3,∴点A的坐标为(2,3).把(-1,-6),(2,3)代入y=ax+b,得解得 ∴一次函数的表达式为y=3x-3.
(2)如图,设直线AB与y轴交于点C,把x=0代入y=3x-3,得y=-3,∴OC=3.∴S△AOB=S△BOC+S△AOC= ×OC·|xB|+ ×OC·xA= ×3×1+ ×3×2= . (3)由ax+b- >0得ax+b> ,
∵直线与双曲线的交点为A(2,3)、B(-1,-6),∴由图象可知,-12时,ax+b- >0.
(1)根据表格中x和y1的对应关系可得,m=　　    ,n=　　    .(2)在平面直角坐标系中,画出该函数的图象.根据函数图象, 写出该函数的一条性质:　　　　　　　    .(3)当函数y1的图象与直线y2=ax+1有三个交点时,直接写出a 的取值范围.
解析    (1)∵y1= ∴x=-2时,m=y1=|2×(-2)+4|=0.∵x=0时,y1=4,∴b=4,∴当x≥0时,y1= ,∴x=3时,n=y1=1.(2)描点、连线,函数图象如图所示(图中实线).
性质:答案不唯一,如:当x<-2时,y随x的增大而减小.(3)0≤a< 或a=-7+4 .【详解】①当直线y=ax+1经过(-2,0)时,a= .
观察图象可知,函数y1的图象与直线y2=ax+1有三个交点时,a 的取值范围为0≤a< ;②由得ax2+(a+1)x-3=0,当Δ=0时,a2+14a+1=0,解得a=-7+4 或-7-4 (舍去).∴a的取值范围为0≤a< 或a=-7+4 .
例题    (2024安徽蚌埠怀远期中)已知点A(-2,y1),点B(1,y2),点 C(3,y3)都在反比例函数y= 的图象上,则 (　    )A.y2变式1.(系数由数字变为字母)(2024安徽合肥四十七中期中)若点 A(-3,y1)、B(-1,y2)、C(3,y3)都在反比例函数y= (k>0)的图象上,则y1、y2、y3的大小关系是 (　    )A.y1>y2>y3　　　B.y3>y1>y2C.y2>y1>y3　　　D.y1>y3>y2
解析　∵反比例函数y= 中,k>0,∴函数图象的两个分支分别位于第一、三象限,且在每一象限内,y随x的增大而减小. ∵-3<-1<0,∴点A(-3,y1),B(-1,y2)位于第三象限,∴y20,∴点C(3,y3)位于第一象限,∴y3>0,∴y3>y1>y2.故选B.
2.(点的横坐标由数字变成字母)(2024安徽阜阳临泉期中)若点(x1,y1)、(x2,y2)和(x3,y3)分别在反比例函数y=- 的图象上,且x1<0解析　由题意,得点(x1,y1)在第二象限,(x2,y2)和(x3,y3)在第四象限,∴y1>0,∵x23.(系数和横坐标都变成字母)(2024安徽六安汇文中学月考) 反比例函数y= 的图象上有三个点(x1,y1),(x2,y2),(x3,y3),其中x1<0

相关课件更多