初中数学华师大版八年级上册5 边边边背景图ppt课件

这是一份初中数学华师大版八年级上册5 边边边背景图ppt课件，共19页。
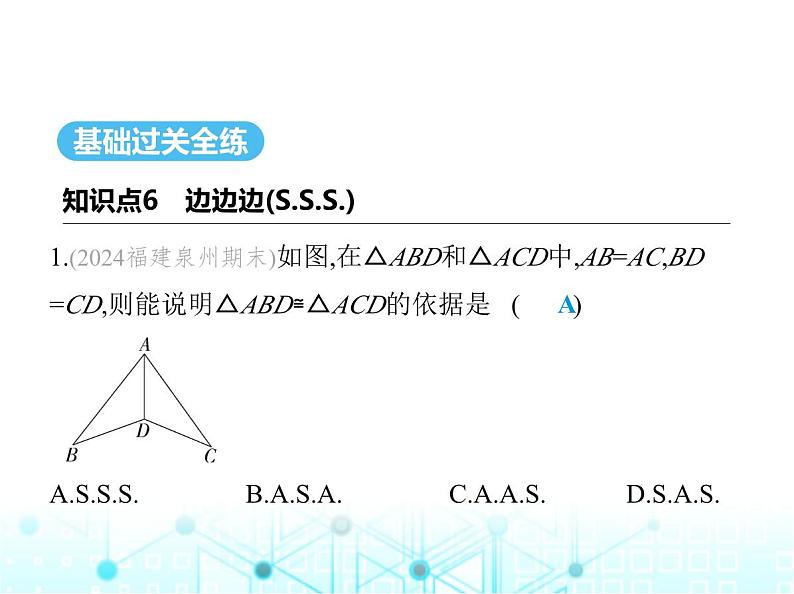
1.(2024福建泉州期末)如图,在△ABD和△ACD中,AB=AC,BD =CD,则能说明△ABD≌△ACD的依据是 (　    ) 　　　    　　　    　　    
解析　在△ABD和△ACD中, ∴△ABD≌△ACD().故选A.
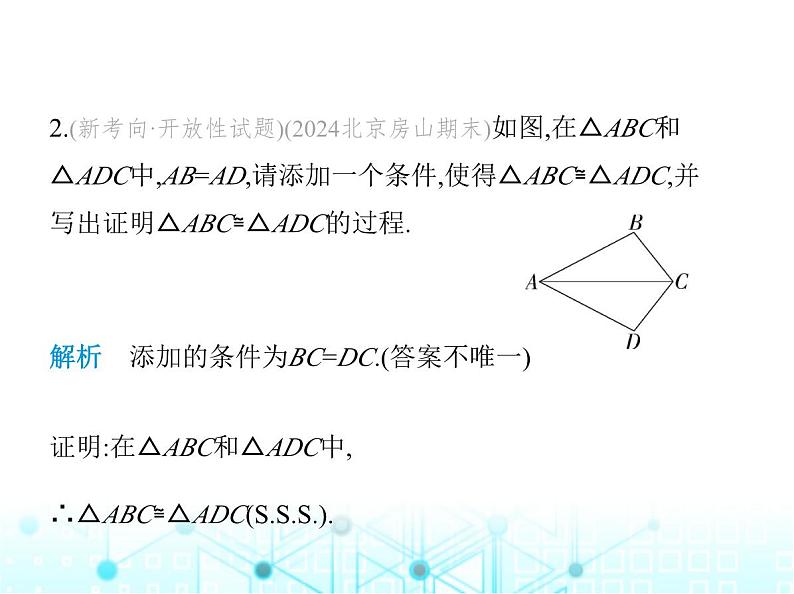
2.(新考向·开放性试题)(2024北京房山期末)如图,在△ABC和 △ADC中,AB=AD,请添加一个条件,使得△ABC≌△ADC,并 写出证明△ABC≌△ADC的过程. 
解析　添加的条件为BC=DC.(答案不唯一)证明:在△ABC和△ADC中, ∴△ABC≌△ADC().
3.(2024广西桂林期末)如图,AB=DC,AC=DB,AC与BD相交于 点O.(1)求证:△ABC≌△DCB.(2)若∠ACB=40°,求∠DOC的度数. 
解析    (1)证明:在△ABC和△DCB中, ∴△ABC≌△DCB().(2)∵△ABC≌△DCB,∴∠ACB=∠DBC,∵∠ACB=40°,∴∠ DBC=∠ACB=40°,∴∠DOC=∠ACB+∠DBC=40°+40°=80°.
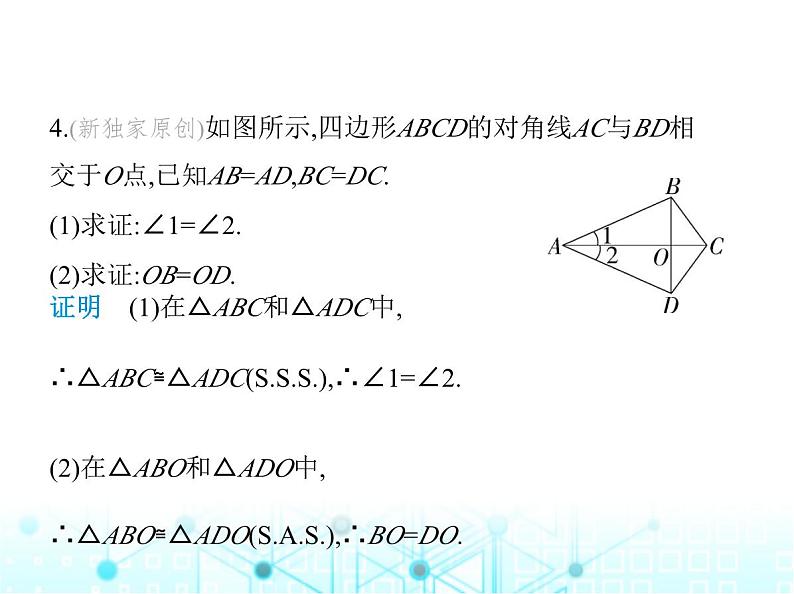
4.(新独家原创)如图所示,四边形ABCD的对角线AC与BD相 交于O点,已知AB=AD,BC=DC.(1)求证:∠1=∠2.(2)求证:OB=OD. 
证明    (1)在△ABC和△ADC中, ∴△ABC≌△ADC(),∴∠1=∠2.(2)在△ABO和△ADO中, ∴△ABO≌△ADO(),∴BO=DO.
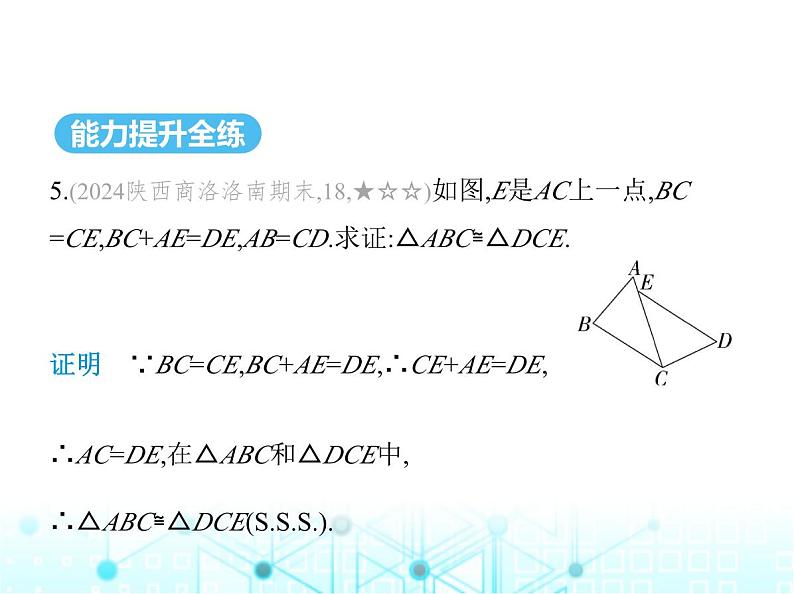
5.(2024陕西商洛洛南期末,18,★☆☆)如图,E是AC上一点,BC =CE,BC+AE=DE,AB=CD.求证:△ABC≌△DCE.
证明　∵BC=CE,BC+AE=DE,∴CE+AE=DE,∴AC=DE,在△ABC和△DCE中, ∴△ABC≌△DCE().
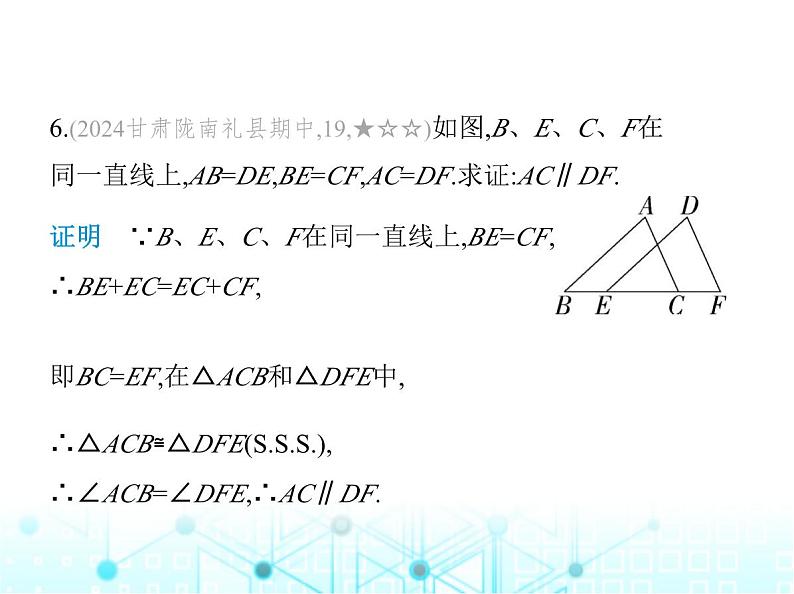
6.(2024甘肃陇南礼县期中,19,★☆☆)如图,B、E、C、F在 同一直线上,AB=DE,BE=CF,AC=DF.求证:AC∥DF. 
证明　∵B、E、C、F在同一直线上,BE=CF,∴BE+EC=EC+CF,即BC=EF,在△ACB和△DFE中, ∴△ACB≌△DFE(),∴∠ACB=∠DFE,∴AC∥DF.
7.(2024吉林长春宽城期末,20,★☆☆)如图,点A、C、D、B 在同一条直线上,点E、F分别在直线AB的两侧,AE=BF,CE= DF,AD=BC.(1)求证:△ACE≌△BDF.(2)若∠CDF=55°,求∠ACE的度数. 
解析    (1)证明:∵AD=BC,∴AD-CD=BC-CD,∴AC=BD,在△ACE和△BDF中, ∴△ACE≌△BDF().(2)由(1)可知△ACE≌△BDF,∴∠ACE=∠BDF,∵∠CDF=5 5°,∴∠BDF=180°-55°=125°,∴∠ACE=125°.
8.(应用意识)(连公共边法)将四根木条首尾相连,在相连处用 螺钉固定,就能构成一个平面图形.(1)若固定三根木条AB,BC,AD不动,AB=AD=2 cm,BC=5 cm, 如图,量得第四根木条CD=5 cm,判断此时∠B与∠D是否相 等,并说明理由.
(2)若固定一根木条AB不动,AB=2 cm,量得木条CD=5 cm,如 果木条AD,BC的长度不变,当点D移到BA的延长线上时,点C 也在BA的延长线上;当点C移到AB的延长线上时,点A、C、 D能构成周长为30 cm的三角形.求木条AD,BC的长度.
解析    (1)相等.理由:连结AC,在△ACD和△ACB中,∵ ∴△ACD≌△ACB(),∴∠B=∠D.(2)设AD=x cm,BC=y cm.假设点C在点D右侧,可得 解得 此时AB+BC=2+10=12(cm),∵CD=5 cm,AD=13
cm,12+5>13,∴符合题意,∴AD=13 cm,BC=10 cm;假设点C在点D左侧,可得 解得 此时AB+BC=2+15=17(cm),∵CD=5 cm,AD=8 cm,8+5=13