数学华师大版第13章 全等三角形13.5 逆命题与逆定理2 线段垂直平分线示范课ppt课件

这是一份数学华师大版第13章 全等三角形13.5 逆命题与逆定理2 线段垂直平分线示范课ppt课件，共24页。

知识点2　线段的垂直平分线的性质定理
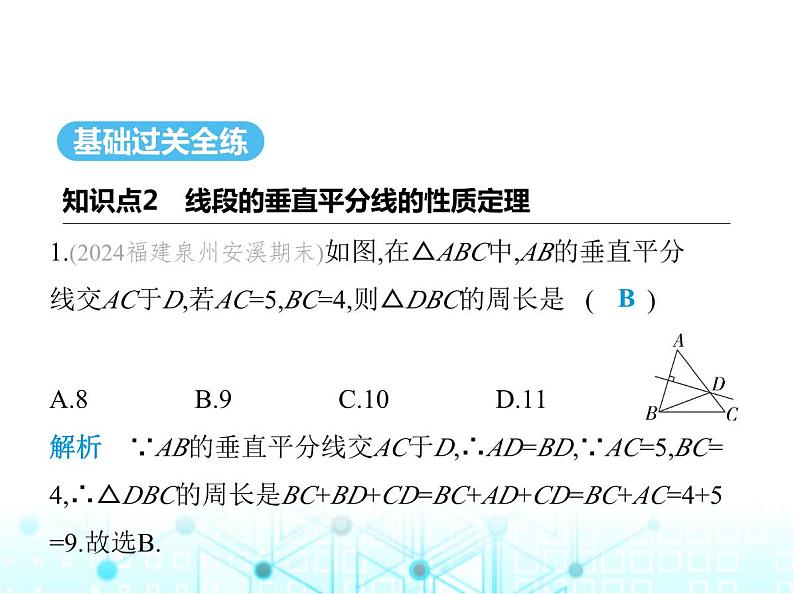
1.(2024福建泉州安溪期末)如图,在△ABC中,AB的垂直平分 线交AC于D,若AC=5,BC=4,则△DBC的周长是 (　    )A.8　　　    B.9　　　    C.10　　　    D.11
解析　∵AB的垂直平分线交AC于D,∴AD=BD,∵AC=5,BC= 4,∴△DBC的周长是BC+BD+CD=BC+AD+CD=BC+AC=4+5 =9.故选B.
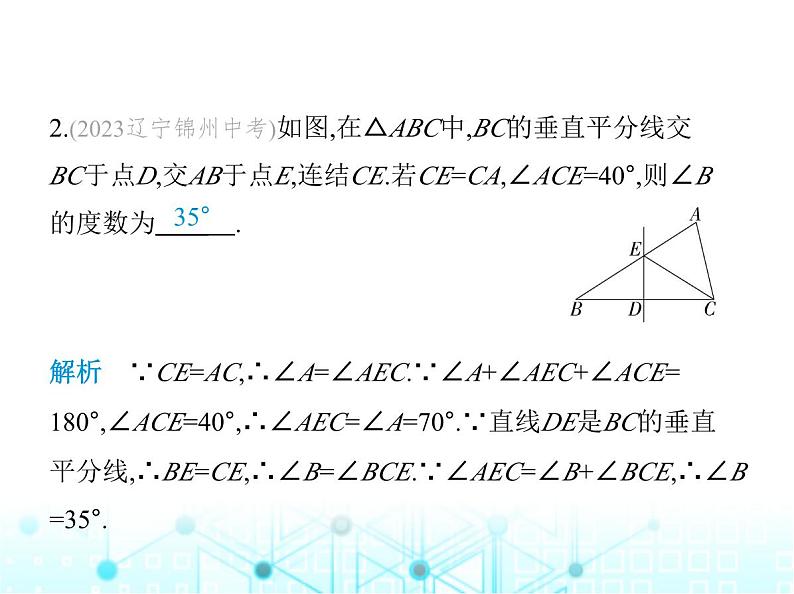
2.(2023辽宁锦州中考)如图,在△ABC中,BC的垂直平分线交 BC于点D,交AB于点E,连结CE.若CE=CA,∠ACE=40°,则∠B 的度数为　　    .
解析　∵CE=AC,∴∠A=∠AEC.∵∠A+∠AEC+∠ACE=180°,∠ACE=40°,∴∠AEC=∠A=70°.∵直线DE是BC的垂直平分线,∴BE=CE,∴∠B=∠BCE.∵∠AEC=∠B+∠BCE,∴∠B =35°.
知识点3　线段的垂直平分线性质定理的逆定理
3.(新独家原创)在“丢沙包”游戏中,A、B、C三名同学站在 一个三角形的三个顶点位置上,要求他们往中间丢沙包,谁丢 到规定的位置,谁就获胜,为使游戏公平,则沙包的最适当的 位置是在△ABC的 (　    )A.三边中线的交点B.三条角平分线的交点C.三边垂直平分线的交点D.三边上高的交点
解析　∵三角形的三条垂直平分线的交点到三角形各顶点 的距离相等,∴沙包最适当的位置是在△ABC的三条垂直平 分线的交点.故选C.
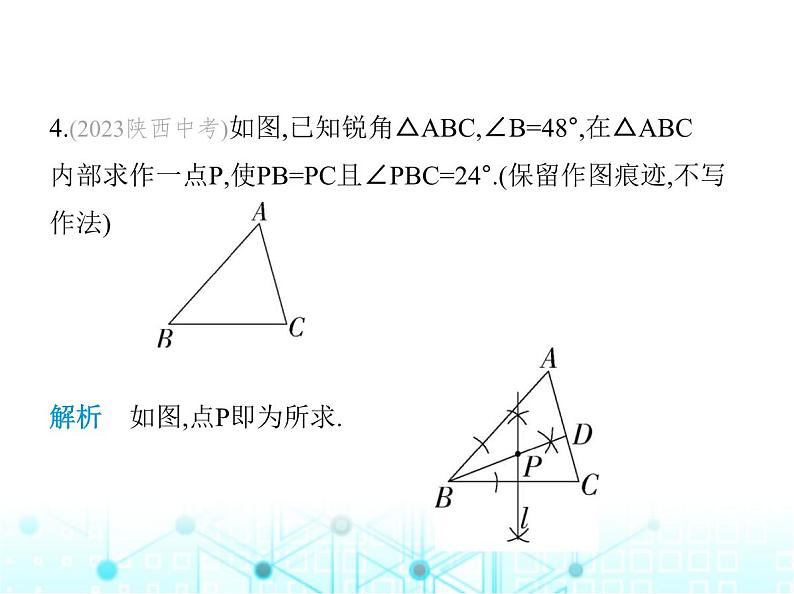
4.(2023陕西中考)如图,已知锐角△ABC,∠B=48°,在△ABC 内部求作一点P,使PB=PC且∠PBC=24°.(保留作图痕迹,不写 作法) 
解析　如图,点P即为所求. 
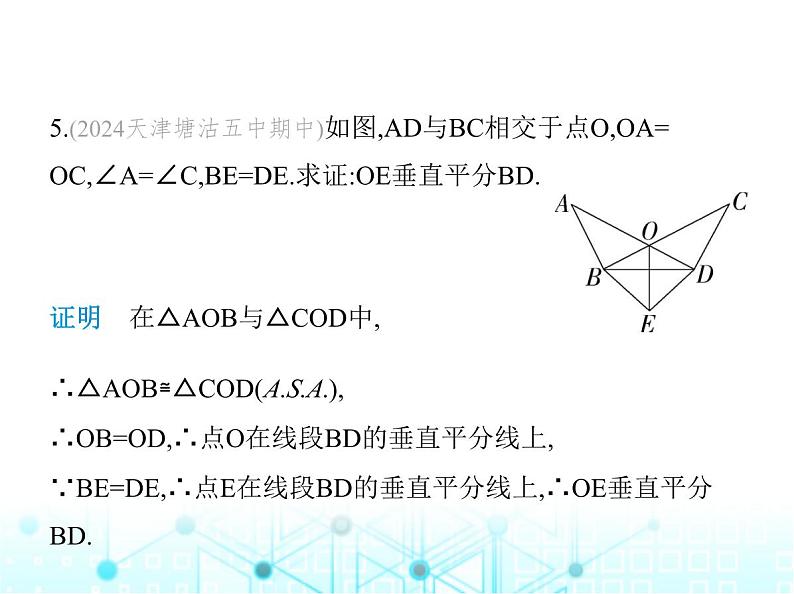
5.(2024天津塘沽五中期中)如图,AD与BC相交于点O,OA= OC,∠A=∠C,BE=DE.求证:OE垂直平分BD. 
证明　在△AOB与△COD中, ∴△AOB≌△COD(),∴OB=OD,∴点O在线段BD的垂直平分线上,∵BE=DE,∴点E在线段BD的垂直平分线上,∴OE垂直平分 BD.
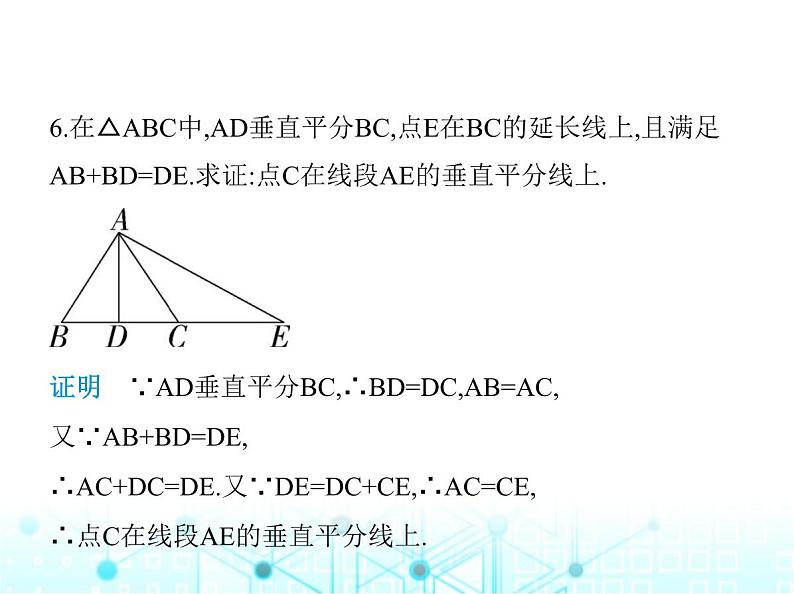
6.在△ABC中,AD垂直平分BC,点E在BC的延长线上,且满足 AB+BD=DE.求证:点C在线段AE的垂直平分线上.
证明　∵AD垂直平分BC,∴BD=DC,AB=AC,又∵AB+BD=DE,∴AC+DC=DE.又∵DE=DC+CE,∴AC=CE,∴点C在线段AE的垂直平分线上.
7.(2021重庆渝中求精中学期末,17,★★☆)如图,P为△ABC 内一点,过点P的线段MN分别交AB、BC于点M、N,且M、N 分别在PA、PC的中垂线上.若∠ABC=80°,则∠APC的度数 为 (　    )A.120°　　　    B.125°　　　    C.130°　　　    D.135°
解析　∵∠ABC=80°,∴∠BMN+∠BNM=180°-80°=100°,∵ M、N分别在PA、PC的中垂线上,∴MA=MP,NC=NP,∴∠ MPA=∠MAP,∠NPC=∠NCP,∴∠MPA+∠NPC= (∠BMN+∠BNM)=50°,∴∠APC=180°-50°=130°.故选C.
8.(2024吉林白城洮城期末,9,★★☆)在△ABC中,边AB,BC 的垂直平分线l1、l2相交于点P,若∠PAC=x°,则∠1的度数是  (　    ) A.90°-x°　　　    B.x°C.90°- x°　　　    D.60°- x°
解析　连结PB、PC,∵边AB,BC的垂直平分线l1、l2相交于 点P,∴PA=PB,PB=PC,∴∠PBA=∠PAB,∠PBC=∠PCB,PA= PC,∴∠PCA=∠PAC=x°,∠PAB+∠PCB=∠PBA+∠PBC=∠ ABC,∴2∠ABC+2x°=180°,∴∠ABC=90°-x°,∴∠DPE=180° -∠ABC=90°+x°,∴∠1=180°-∠DPE=90°-x°,故选A. 
9.(2024河南信阳罗山期中,21,★★☆)如图,在△ABC中,∠ABC=45°,CD⊥AB于点D,AC的垂直平分线BE与CD交于点F,与AC交于点E.(1)判断△DBC的形状并证明你的结论.(2)求证:BF=AC.(3)试说明CE= BF. 
解析    (1)△DBC是等腰直角三角形.证明:∵∠ABC=45°,CD⊥AB,∴∠BCD=45°,∴BD=CD,∴△DBC是等腰直角三角形.(2)证明:∵BE⊥AC,CD⊥AB,∴∠BDC=∠BEC=∠ADC=90°,∵∠BFD=∠CFE,∴∠DBF=∠ACD,在△BDF与△CDA中, ∴△BDF≌△CDA(),∴BF=AC.
(3)证明:∵BE所在直线是AC的垂直平分线,∴CE= AC,∴CE= BF.
10.(新考向·开放性试题)(2023江苏泰州中考,20,★★☆)如图, CD是五边形ABCDE的一边,若AM垂直平分CD,垂足为M,且 　　　    ,　　　    ,则　　　    .给出下列信息:①AM平分∠BAE;②AB=AE;③BC=DE.请从中 选择适当信息,将对应的序号填到横线上方,使之构成真命 题,补全图形,并加以证明. 
解析　②;③;①(或①;②;③,选择一种即可).选择②;③;①.证明:根据题意补全图形并连结AC、AD,如图所示:∵AM垂直平分CD,∴AC=AD,∴∠CAM=∠DAM,在△ABC与 △AED中, ∴△ABC≌△AED(),∴∠BAC=∠EAD,∴∠BAC+∠CAM=∠EAD+∠DAM,即∠BAM=∠EAM=  ∠BAE,∴AM平分∠BAE.
 选择①;②;③.证明:根据题意补全图形并连结AC、AD,如图所示:∵AM垂直平分CD,∴AC=AD, ∴∠CAM=∠DAM,∵AM平分 ∠BAE,∴∠BAM=∠EAM,∴∠BAM-∠CAM=∠EAM-∠DAM,即∠ BAC=∠EAD,
在△ABC与△AED中, ∴△ABC≌△AED(),∴BC=DE.
11.(推理能力)(新考向·过程性学习试题)如图,在△ABC中,边 AB的垂直平分线l1交BC于点D,边AC的垂直平分线l2交BC于 点E,l1与l2相交于点O.(1)如图1,当∠ABC=∠ACB=25°时,直接写出∠DAE的度数.(2)如图1,当AB≠AC,且90°≤∠BAC<180°时.①若∠BAC=120°,则∠DAE=　　　    °.②当AD⊥AE时,求∠BAC的度数.(3)如图2,连结OA,OB,OC.若△ADE的周长为9 cm,△OBC的 周长为21 cm,则BC=　　　    cm,OB=　　　    cm.
  图1 图2
解析    (1)80°.(2)①∵l1垂直平分AB,∴DA=DB,∴∠BAD=∠B,同理∠EAC=∠C,∴∠BAD+∠EAC=∠B+∠C,∵∠BAC=120°,∴∠B+∠C=60°,∴∠BAD+∠EAC=60°,∴∠DAE=∠BAC-(∠BAD+∠EAC)=120°-60°=60°.②∵AD⊥AE,∴∠DAE=90°,∵l1垂直平分AB,∴DA=DB,∴∠BAD=∠B,同理∠EAC=∠C,
∴∠BAD+∠EAC=∠B+∠C,∵∠BAD+∠EAC+∠B+∠C+∠DAE=180°,∴∠BAD+∠EAC=(180°-90°)× =45°,∴∠BAC=∠BAD+∠EAC+∠DAE=90°+45°=135°.(3)∵l1垂直平分AB,∴DA=DB,OB=OA,同理EA=EC,OC=OA,∴DA+DE+EA=BD+DE+EC=BC,∵△ADE的周长是9 cm,∴BC=9 cm,