华师大版八年级上册2 直角三角形的判定教学课件ppt

这是一份华师大版八年级上册2 直角三角形的判定教学课件ppt，共21页。PPT课件主要包含了基础过关全练，能力提升全练，素养探究全练等内容，欢迎下载使用。

知识点3　直角三角形的判定——勾股定理的逆定理
1.(2024重庆北碚期末)下列长度的三条线段能组成直角三角 形的是 (　    )A.1,1, 　　　    B.2,3,4C.4,5,6　　　    D.6,8,11
解析　∵12+12=( )2,∴长为1,1, 的三条线段能组成直角三角形,故A选项正确;∵22+32≠42,∴长为2,3,4的三条线段不 能组成直角三角形,故B选项错误;∵42+52≠62,∴长为4,5,6的 三条线段不能组成直角三角形,故C选项错误;∵62+82≠112, ∴长为6,8,11的三条线段不能组成直角三角形,故D选项错 误.故选A.
2.(2024山东济南章丘期末)△ABC的三边长分别为a,b,c且(a +b)(a-b)=c2,则该三角形是 (　    )A.以a为斜边长的直角三角形B.以b为斜边长的直角三角形C.以c为斜边长的直角三角形D.锐角三角形
解析　∵(a+b)(a-b)=c2,∴a2-b2=c2,∴c2+b2=a2,∴△ABC是以a 为斜边长的直角三角形.故选A.
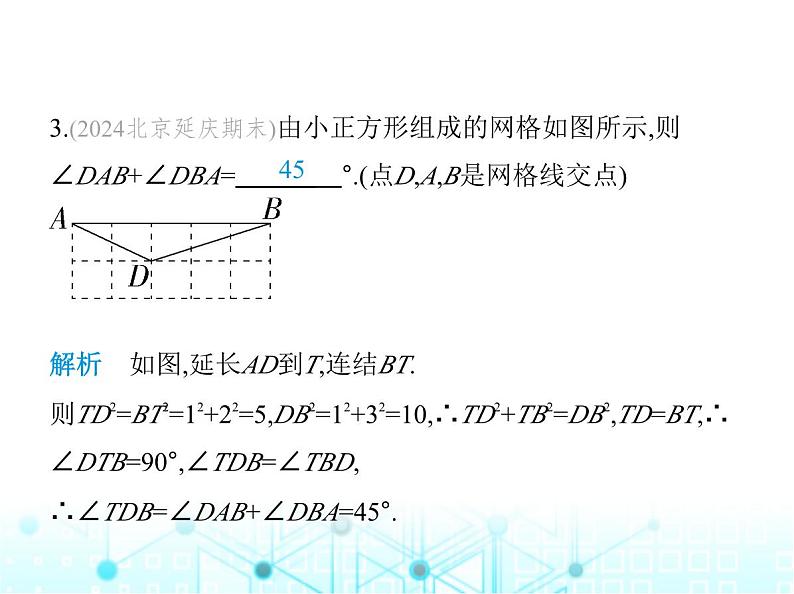
3.(2024北京延庆期末)由小正方形组成的网格如图所示,则 ∠DAB+∠DBA=　　　    °.(点D,A,B是网格线交点)
解析　如图,延长AD到T,连结BT.则TD2=BT2=12+22=5,DB2=12+32=10,∴TD2+TB2=DB2,TD=BT,∴ ∠DTB=90°,∠TDB=∠TBD,∴∠TDB=∠DAB+∠DBA=45°.
4.(等积法求面积)(2023河南南阳内乡期末)一个三角形的三 边长分别为5,12,13,则这个三角形最长边上的高为　　　    .
解析　∵三角形的三边长分别为5,12,13,且52+122=132,∴此 三角形为直角三角形,且13为直角三角形的斜边长,设斜边上 的高为h,则 h·13= ×5×12,解得h= .
5.(分类讨论思想)已知两条线段的长为5 cm和12 cm,当第三 条线段的长为　　　    cm时,这三条线段能组成一个直角三 角形.
解析　当12 cm为直角边长时,根据勾股定理得第三条线段 的长为 =13 cm;当12 cm为斜边长时,第三条线段的长为 =  cm.故答案为13或 .
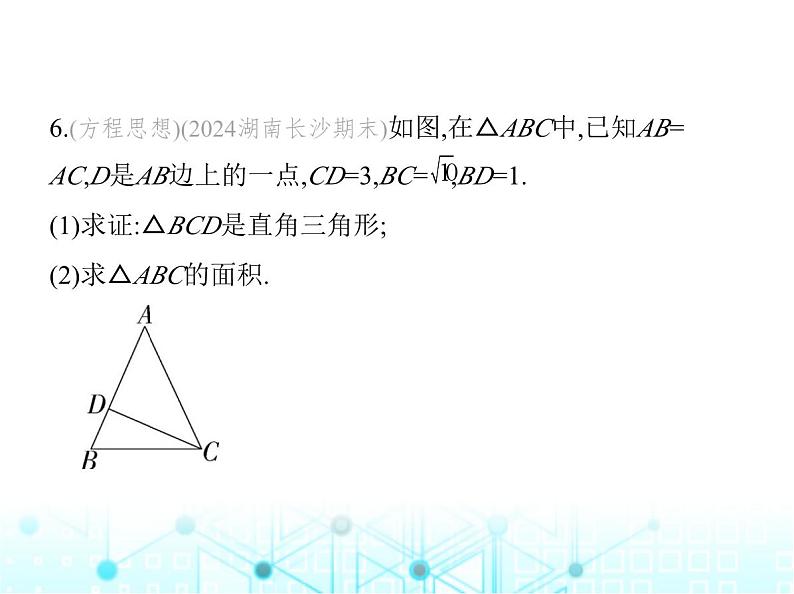
6.(方程思想)(2024湖南长沙期末)如图,在△ABC中,已知AB= AC,D是AB边上的一点,CD=3,BC= ,BD=1.(1)求证:△BCD是直角三角形;(2)求△ABC的面积. 
解析    (1)证明:∵CD=3,BC= ,BD=1,∴CD2+BD2=32+12=10=BC2,∴△BCD是直角三角形.(2)由(1)易知,△BCD是直角三角形,且∠BDC=90°,∴∠ADC= 90°,设AC=x,则AB=AC=x,∴AD=x-1,∵CD2+AD2=AC2,∴32+(x-1)2=x2,解得x=5,∴AB=AC=5,∴△ABC的面积是 = = .
7.(新独家原创)在△ABC中,∠A,∠B,∠C的对边长分别为a、 b、c,且满足a2+|c-10|+ =12a-36,试判断△ABC的形状.
解析　∵a2+|c-10|+ =12a-36,∴a2-12a+36+|c-10|+ =0,∴(a-6)2+|c-10|+ =0,∴a-6=0,c-10=0,b-8=0,∴a=6,c=10,b=8.∴a2+b2=62+82=100,c2=102=100,∴c2=a2+b2,∴△ABC是直角三角形,且∠C=90°.
8.(情境题·数学文化)(2024广东深圳福田红岭中学期末)勾股 定理被记载于我国古代著名的数学著作《周髀算经》中.下 列各组数中,是勾股数的是 (　    )A.0.3,0.4,0.5　　　    B.4,5,6C.7,8,9　　　    D.6,8,10
解析    0.3,0.4,0.5不是正整数,故不是勾股数;42+52≠62,故4,5, 6不是勾股数;72+82≠92,故7,8,9不是勾股数;82+62=102,且6,8,10是正整数,故是勾股数.故选D.
9.(新考向·规律探究试题)(2024湖南衡阳期末)勾股定理a2+b2 =c2本身就是一个关于a,b,c的方程,满足这个方程的正整数解 (a,b,c)通常叫做勾股数组.毕达哥拉斯学派提出了一个构造 勾股数组的公式,根据该公式可以构造出如下勾股数组:(3,4, 5),(5,12,13),(7,24,25),……分析上面的勾股数组可以发现,4= 1×(3+1),12=2×(5+1),24=3×(7+1),……则第5个勾股数组为     　　    . 
解析　由勾股数组(3,4,5),(5,12,13),(7,24,25),……中4=1×(3+1),12=2×(5+1),24=3×(7+1),……可得第4个勾股数组 中间的数为4×(9+1)=40,即第4个勾股数组为(9,40,41);第5个勾股数组中间的数为5×(11+1)=60,即第5个勾股数组为 (11,60,61).
10.(2024四川巴中期末,9,★★☆)若△ABC的三边长分别是a, b,c,则下列条件:①∠A+∠B=∠C;②a∶b∶c=5∶12∶13;③ ∠A∶∠B∶∠C=3∶4∶5;④b2=(a+c)(a-c).不能判定△ABC 是直角三角形的有 (　    )A.1个　　　    B.2个　　　    C.3个　　　    D.4个
解析　①∵∠A+∠B=∠C,∠A+∠B+∠C=180°,∴∠C=90°, 故△ABC是直角三角形;②∵a∶b∶c=5∶12∶13,∴可设a=5 k,b=12k,c=13k,∵(5k)2+(12k)2=(13k)2,∴a2+b2=c2,故△ABC是 直角三角形;③∵∠A∶∠B∶∠C=3∶4∶5,∴最大角∠C=  ×180°=75°,故△ABC不是直角三角形;④∵b2=(a-c)(a+c)=a2-c2,∴b2+c2=a2,故△ABC是直角三角形.综上,不能判定 △ABC是直角三角形的有1个.故选A.
11.(新考法)(2023山东济宁中考,9,★★☆)如图,在正方形方 格中,每个小正方形的边长都是一个单位长度,点A,B,C,D,E 均在小正方形方格的顶点上,线段AB,CD交于点F,若∠CFB= α,则∠ABE等于 (　    ) A.180°-α　　 　    B.180°-2αC.90°+α　　　     D.90°+2α
解析　本题将直角三角形的判定与平行线的性质联系在一 起考查,比较新颖.如图,过B点作BG∥CD,连结EG,∵BG∥ CD,∴∠ABG=∠CFB=α.∵BG2=12+42=17,BE2=12+42=17,EG2 =32+52=34,∴BG2+BE2=EG2,∴△BEG是直角三角形,∴∠GBE=90°,∴∠ABE=∠GBE+∠ABG=90°+α.故选C.
12.(新考向·新定义试题)(2024四川成都圣菲学校月考,23,★★☆)满足a2+b2=c2的三个正整数,称为勾股数.若正整数a,n满足a2+n2=(n+1)2,则称三个正整数a,n,n+1(如:3,4,5或5,12,13)为一组“完美勾股数”,当n<115时,共有 　　　    组这样的“完美勾股数”.
解析　∵a2+n2=(n+1)2,∴a2=(n+1)2-n2=2n+1,∴a2为奇数,且为 完全平方数,∵n<115,∴2n+1<231,∴a2<231,∴a2为231以内的奇数,且为完全平方数,有9,25,49,81,121,16 9,225,一共7个,∴共有7组这样的“完美勾股数”.
13.(推理能力)阅读下列解题过程:已知a、b、c为△ABC的三边长,且满足a2c2-b2c2=a4-b4,试判断 △ABC的形状.解:因为a2c2-b2c2=a4-b4,①所以c2(a2-b2)=(a2-b2)(a2+b2).②所以c2=a2+b2.③所以△ABC是直角三角形.回答下列问题:
(1)上述解题过程,从哪一步开始出现错误?请写出该步的序号:　　　    .(2)错误的原因为　　　 　　　　    .(3)请你将正确的解答过程写下来.
忽略了a2-b2=0的可能.