华东师大版初中八年级数学上册专项素养综合练(五)几何动态问题与全等三角形课件

这是一份华东师大版初中八年级数学上册专项素养综合练(五)几何动态问题与全等三角形课件，共21页。

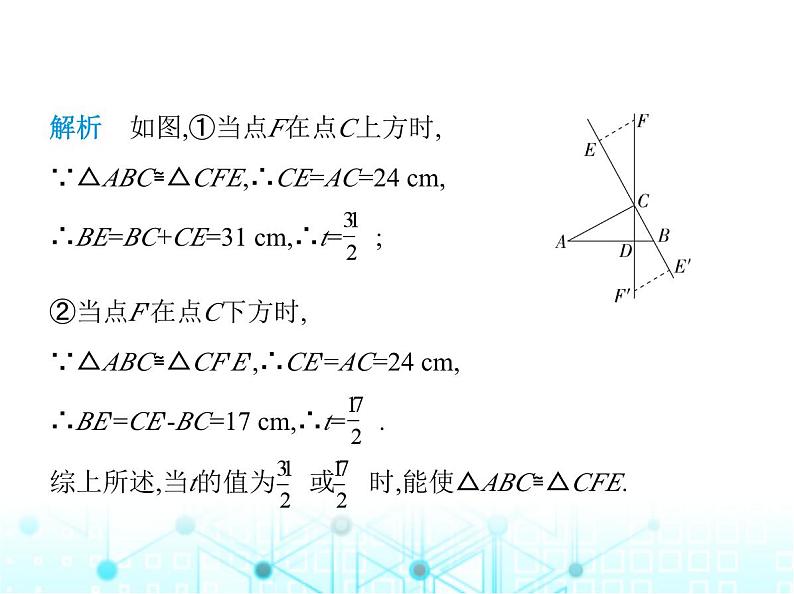
专项素养综合全练(五)几何动态问题与全等三角形1.(2024海南海口华侨中学期中)如图,在长方形ABCD中,AB=题型一　动点问题10 cm,点E在线段AD上,且AE=6 cm,动点P在线段AB上,从点A出发以2 cm/s的速度向点B运动,同时点Q在线段BC上,以v cm/s的速度由点B向点C运动,当△EAP与△PBQ全等时,v的值为 (　    )A.2　　　    B.4C.4或 　　　    D.2或  D解析　△EAP与△PBQ全等,有两种情况:①当EA=PB时,△APE≌△BQP,∴BQ=AP,∵AB=10 cm,AE=6 cm,∴BP=AE=6 cm,∴AP=4 cm,∴BQ=AP=4 cm,∵动点P在线段AB上,从点A出发以2 cm/s的速度向点B运动,∴点P和点Q的运动时间为4÷2=2 s,∴v的值为4÷2=2;②当AP=BP时,△AEP≌△BQP,∴BQ=AE,∵AB=10 cm,AE=6 cm,∴AP=BP=5 cm,BQ=AE=6 cm,∵动点P在线段AB上,从点A出发以2 cm/s的速度向点B运动,∴点P和点Q的运动时间为5÷2=2.5 s,∴v的值为 = .综上,v的值为2或 .故选D.2.(2024河南南阳淅川期中)如图,在Rt△ABC中,∠ACB=90°,BC=7 cm,AC=24 cm,AB=25 cm,CD为AB边上的高,直线CD上一点F满足CF=AB,点E从点B出发,在直线BC上朝固定方向以2 cm/s的速度移动,设运动时间为t秒,当t=　　　    时,能使△ABC≌△CFE.解析　如图,①当点F在点C上方时,∵△ABC≌△CFE,∴CE=AC=24 cm,∴BE=BC+CE=31 cm,∴t= ;②当点F'在点C下方时,∵△ABC≌△CF'E',∴CE'=AC=24 cm,∴BE'=CE'-BC=17 cm,∴t= .综上所述,当t的值为 或 时,能使△ABC≌△CFE.3.(2024重庆九龙坡期末)如图,在△ABC中,∠ACB=90°,AC=6,BC=8.点P从点A出发,沿折线AC-CB以每秒1个单位长度的速度向终点B运动,点Q从点B出发沿折线BC-CA以每秒3个单位长度的速度向终点A运动,P、Q两点同时出发,当其中一点到达终点时,另一点立刻停止运动.分别过P、Q两点作PE⊥l于E,QF⊥l于F,当△PEC与△QFC全等时,求CQ的长.  解析　设运动时间为t秒,当P在AC上,Q在BC上时,∵∠ACB=90°,∴∠PCE+∠QCF=90°,∵PE⊥l于E,QF⊥l于F,∴∠PEC=∠CFQ=90°,∴∠EPC+∠PCE=90°,∴∠EPC=∠QCF,分析易得△PCE≌△CQF,∴PC=CQ,∴6-t=8-3t,解得t=1,∴CQ=8-3t=5;当P在AC上,Q在AC上时,分析易得P、Q重合时,△PCE≌△QCF,则CQ=PC,由题意得6-t=3t-8,解得t=3.5,∴CQ=3t-8=2.5;当点Q与点A重合,点P运动到BC上时,分析易得△PCE≌△CQF,此时CQ=AC=CP=6.综上,当△PEC与△QFC全等时,CQ的长为5或2.5或6.题型二　半角型4.(2023山西大同平城中学校月考)定义:过等腰三角形顶角的顶点引两条射线,使两条射线的夹角为等腰三角形顶角的一半,这样的模型称为“半角模型”.常见的图形有正方形、正三角形、等腰直角三角形等,在解决“半角模型”的问题时,旋转是一种常用的方法.已知,如图1,四边形ABCD是正方形,E,F分别在边BC、CD上,且∠EAF=45°,(1)在图1中,连结EF,为了证明结论“EF=BE+DF”,小亮将△ADF绕点A顺时针旋转90°后解答了这个问题,请按小亮的思路写出证明过程.(2)当∠EAF绕点A旋转到图2的位置时,试探究EF与DF、BE之间有怎样的数量关系.  图1 图2解析    (1)证明:如图,由旋转可得GB=DF,AF=AG,∠BAG=∠DAF,∠ABG=∠ADF,∵四边形ABCD为正方形,∴∠BAD=∠ADF=∠ABC=90°,∴∠ABC+∠ABG=180°,∴G,B,C三点在一条直线上,∵∠EAF=45°,∴∠BAE+∠DAF=45°,∴∠BAG+∠BAE=45°=∠EAG,∴∠EAG=∠EAF,在△AGE和△AFE中, ∴△AGE≌△AFE(S.A.S.),∴GE=EF,∵GE=GB+BE=BE+DF,∴EF=BE+DF.(2)如图,把△ABE绕点A逆时针旋转90°,使AB与AD重合,点E与点G对应,∴△ABE≌△ADG,∴BE=DG,与(1)同理可证得△AEF≌△AGF(S.A.S.),∴EF=GF,∴EF=GF=DF-DG=DF-BE,即EF=DF-BE.5.如图,在四边形ABCD中,AB=AD,∠B=∠D=90°,∠BAD=120°,以A为顶点的∠EAF=60°,AE、AF与BC、CD边分别交于E、F两点.求证:EF=BE+DF.  证明　如图,将△ADF绕点A顺时针旋转120°得到△ABM,∴△ABM≌△ADF,∠ABM=∠D=90°,∠MAB=∠FAD,AM=AF,MB=DF,∴∠MBE=∠ABM+∠ABE=180°,∴M、B、E三点共线,∵∠MAE=∠MAB+∠BAE=∠FAD+∠BAE=∠BAD-∠EAF=60°,∴∠MAE=∠FAE,又∵AE=AE,AM=AF,∴△MAE≌△FAE(S.A.S.),∴ME=EF,∴EF=ME=MB+BE=DF+BE,即EF=BE+DF.题型三　平移型6.(2024河南驻马店西平月考)如图,已知△ABC≌△DEF,∠A=75°,∠ABC=60°,AB=8,BD=3.求∠DHB的度数与BE的长.  解析　∵∠A=75°,∠ABC=60°,∴∠ACB=180°-∠A-∠ABC=45°,∵△ABC≌△DEF,∴∠EDF=∠A=75°,DE=AB=8,∵∠ABC=60°,BD=3,∴∠DHB=180°-∠ABC-∠EDF=45°,BE=8-3=5.7.(新考向·开放性试题)(2024浙江杭州西湖期末)如图,在△ABC和△DEF中,点B,E,C,F在同一条直线上,已知∠B=∠DEF,BE=CF.下面给出四个条件:①AC=DF;②AB=DE;③AC∥DF;④∠A=∠D.请你从中任选一个条件,使得△ABC≌△DEF,并写出证明过程.解析　选②AB=DE.证明:∵BE=CF,∴BC=EF,在△ABC与△DEF中, ∴△ABC≌△DEF(S.A.S.).(答案不唯一)题型四　翻折型8.(2024福建泉州惠安第四联盟期中)如图,已知OD=OE,那么添加下列条件后,仍无法判定△OBD≌△OCE的是 (　    ) A.OB=OC　　　    B.∠D=∠EC.∠DBO=∠ECO　　　    D.BD=CED解析    A.添加OB=OC,根据S.A.S.可以判定△OBD≌△OCE.B.添加∠D=∠E,根据A.S.A.可以判定△OBD≌△OCE.C.添加∠DBO=∠ECO,根据A.A.S.可以判定△OBD≌△OCE.D.添加BD=EC,无法判定△OBD≌△OCE.故选D.9.(2024河南鹤壁淇滨第三次月考)如图,在正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G,连结AG.求证:△ABG≌△AFG.  证明　∵四边形ABCD是正方形,∴∠B=∠D=90°,AD=AB,由折叠的性质可知AD=AF,∠AFE=∠D=90°,∴∠AFG=90°=∠B,AB=AF,在Rt△ABG和Rt△AFG中, ∴Rt△ABG≌Rt△AFG(H.L.).