初中数学华师大版八年级上册1 直角三角形三边的关系课堂教学课件ppt

这是一份初中数学华师大版八年级上册1 直角三角形三边的关系课堂教学课件ppt，共20页。PPT课件主要包含了基础过关全练，能力提升全练，素养探究全练等内容，欢迎下载使用。

1.在Rt△ABC中,∠C=90°,BC=12,AC=16,则AB的长为 (        )A.26　　　    B.18　　　    C.20　　　    D.21
解析　∵Rt△ABC中,∠C=90°,BC=12,AC=16,∴AB=  = =20.故选C.
2.在Rt△ABC中,a,b,c分别是∠A,∠B,∠C的对边长,若∠A=9 0°,则 (　    )A.a2+b2=c2　　　    B.b2+c2=a2C.a2+c2=b2　　　    D.b+a=c
解析　∵在Rt△ABC中,a,b,c分别是∠A,∠B,∠C的对边长, ∠A=90°,∴a为斜边长,∴b2+c2=a2.故选B.
3.(新考法)(2024辽宁沈阳大东期末)已知Rt△ABC中,∠C=90°,a,b,c分别是∠A、∠B、∠C的对边长,若a+b=14,c=10,则△ABC的面积为 (　    )A.48　　　    B.24　　　    C.96　　　    D.20
解析　∵∠C=90°,c=10,∴a2+b2=c2=100,∵a+b=14,∴(a+b)2= 196,∴2ab=196-(a2+b2)=96,∴ab=48,∴△ABC的面积= ab= ×48=24.故选B.
4.(数形结合思想)如图,直线AO⊥OB,垂足为O,线段AO=6,BO =8,以点A为圆心,AB的长为半径画弧,交直线AO于点C,则OC 的长为 (　    )A.10　　　    B.8　　　    C.6　　　    D.4
解析　∵AO⊥OB,∴∠AOB=90°,∵AO=6,BO=8,∴AB=  = =10,∴AC=AB=10,∴OC=AC-AO=10-6=4.故选D.
5.(勾股树模型)(2021四川成都中考)如图,数字代表所在正方 形的面积,则A所代表的正方形的面积为　　　    . 
解析　由题意可知,直角三角形中,一条直角边长的平方=36, 另一条直角边长的平方=64,则斜边长的平方=36+64=100,即 A所代表的正方形的面积为100.
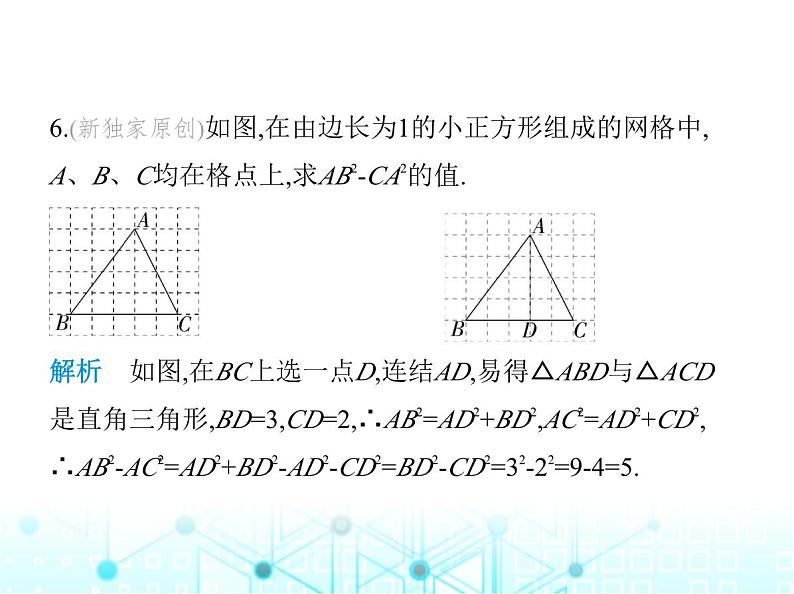
6.(新独家原创)如图,在由边长为1的小正方形组成的网格中, A、B、C均在格点上,求AB2-CA2的值. 
解析　如图,在BC上选一点D,连结AD,易得△ABD与△ACD 是直角三角形,BD=3,CD=2,∴AB2=AD2+BD2,AC2=AD2+CD2, ∴AB2-AC2=AD2+BD2-AD2-CD2=BD2-CD2=32-22=9-4=5. 
7.(设参数法)(2024江西吉安泰和期末)若直角三角形两直角 边长的比是3∶4,斜边长为20 cm,求斜边上的高.
解析　设两直角边长分别为3x cm和4x cm,斜边上的高为y cm,依题意得(3x)2+(4x)2=202,解得x=4(舍负),∴3x=12,4x=16,∴ y·20= ×12×16,∴y=9.6.∴斜边上的高为9.6 cm.
知识点2　勾股定理的证明
8.(2023江苏苏州月考)如图,四边形ABCD中,BD⊥CD于点D, AE⊥BD于点E,且△ABE≌△BCD.求证:AB2=BE2+AE2. 
证明　如图,连结AC.
∵AE⊥BD,CD⊥BD,∴AE∥CD.∵△ABE≌△BCD,∴AB=BC,AE=BD,BE=CD,∠BAE=∠CBD.∵∠ABE+∠BAE=90°,∴∠ABE+∠CBE=90°,∴∠ABC=90°,∴S四边形ABCD=S△ABD+S△BDC= BD·AE+ BD·CD= AE·AE+ BD·BE= AE2+ BD·BE.
又∵S四边形ABCD=S△ABC+S△ADC= AB·BC+ CD·DE= AB·AB+ BE·DE= AB2+ BE·DE,∴ AE2+ BD·BE= AB2+ BE·DE,∴AB2=AE2+BD·BE-BE·DE,∴AB2=AE2+(BD-DE)·BE,即AB2=BE2+AE2.
9.(数形结合思想)(2024吉林长春新区期末,9,★★☆)如图,数 轴上点A表示的数为-1,Rt△ABC的直角边AB落在数轴上,且 AB长为3个单位长度,BC长为1个单位长度,若以点A为圆心, 以斜边AC长为半径画弧交数轴于点D,则点D表示的数为 (　    )A. 　　　    B. -1　　　    C. 　　　    D. -1
解析　由勾股定理知AC= = = ,所以AD=AC= .所以点D表示的数为 -1.故选D.
10.(2023天津中考,10,★★☆)如图,在△ABC中,分别以点A 和点C为圆心,大于 AC的长为半径作弧(弧所在圆的半径都相等),两弧相交于M,N两点,直线MN分别与边BC,AC相交于 点D,E,连结AD.若BD=DC,AE=4,AD=5,则AB的长为 (　    ) A.9　　　    B.8　　　    C.7　　　    D.6
解析　由题意得,直线MN是AC的垂直平分线,∴AC=2AE=8, DA=DC,∴∠DAC=∠C,∵BD=CD,∴BD=AD,∴∠B=∠BAD,∵∠B+∠BAD+∠C+∠DAC=180°,∴2∠BAD+2∠DAC=180°,∴∠BAD+∠DAC=90°,∴∠BAC=90°, 在Rt△ABC中,BC=BD+CD=2AD=10,∴AB= =
11.(2024河南南阳方城期末,12,★☆☆)在△ABC中,AB=AC, AD是BC边上的中线,若AB=10,BC=12,则AD的长为　　      .
解析　∵AB=AC,AD是BC边上的中线,∴AD⊥BC,BD= BC=6,在Rt△ABD中,AB=10,BD=6,由勾股定理,得AD= = =8.
12.(应用意识)(一线三垂直模型)(2024四川成都西川中学期末)数与形是数学中的两个最古老,也是最基本的研究对象. 数与形也是有联系的,这种联系称为“数形结合”.利用“数 形结合”思想可以直观地帮助我们解决一些数学验证或运算.(1)勾股定理阐明了直角三角形的三边关系.请你利用下图对 勾股定理(即下列命题)进行验证,从中体会“数形结合”的 思想.已知:如图,在Rt△ABC和Rt△CDE中,∠B=∠D=∠ACE=90°,
点B,C,D在一条直线上,AB=b,BC=a,AC=EC=c.证明:a2+b2=c2.(2)请利用“数形结合”思想,画图推算出(a+b+c)2的结果
解析    (1)证明:梯形ABDE的面积=2× ab+ c2,梯形ABDE的面积= ,∴2× ab+ c2= ,∴ab+ c2= (a2+2ab+b2),∴ab+ c2= a2+ab+ b2,∴ c2= a2+ b2,∴a2+b2=c2.(2)如图,大正方形的面积=(a+b+c)2,