福建省泉州第一中学2024届九年级下学期第一次月考数学试卷(含解析)

这是一份福建省泉州第一中学2024届九年级下学期第一次月考数学试卷(含解析)，共21页。试卷主要包含了选择题，解答题等内容，欢迎下载使用。
一、选择题（本大题共10个小题，每小题4分，共40分）
1. ﹣6的相反数是（ ）
A. ﹣6B. ﹣C. 6D.
答案：C
解析：
详解：解：的相反数是6，
故选：C．
2. 第33届夏季奥运会将于2024年7月26日至8月11日在法国巴黎举行，下列巴黎奥运会项目图标中，轴对称图形是（ ）
A. B. C. D.
答案：B
解析：
详解：解：A、不是轴对称图形，故此选项不符合题意；
B、是轴对称图形，故此选项符合题意；
C、不是轴对称图形，故此选项不符合题意；
D、不是轴对称图形，故此选项不符合题意；
故选：B．
3. 中国立足本国国情、粮情，实施新时期国家粮食安全战略，走出了一条中国特色粮食安全之路．2022年我国全年粮食产量68653万吨，比上年增加368万吨，增产．将686530000用科学记数法表示应为（ ）
A. B. C. D.
答案：C
解析：
详解：解：686530000用科学记数法表示应为．
故选：C．
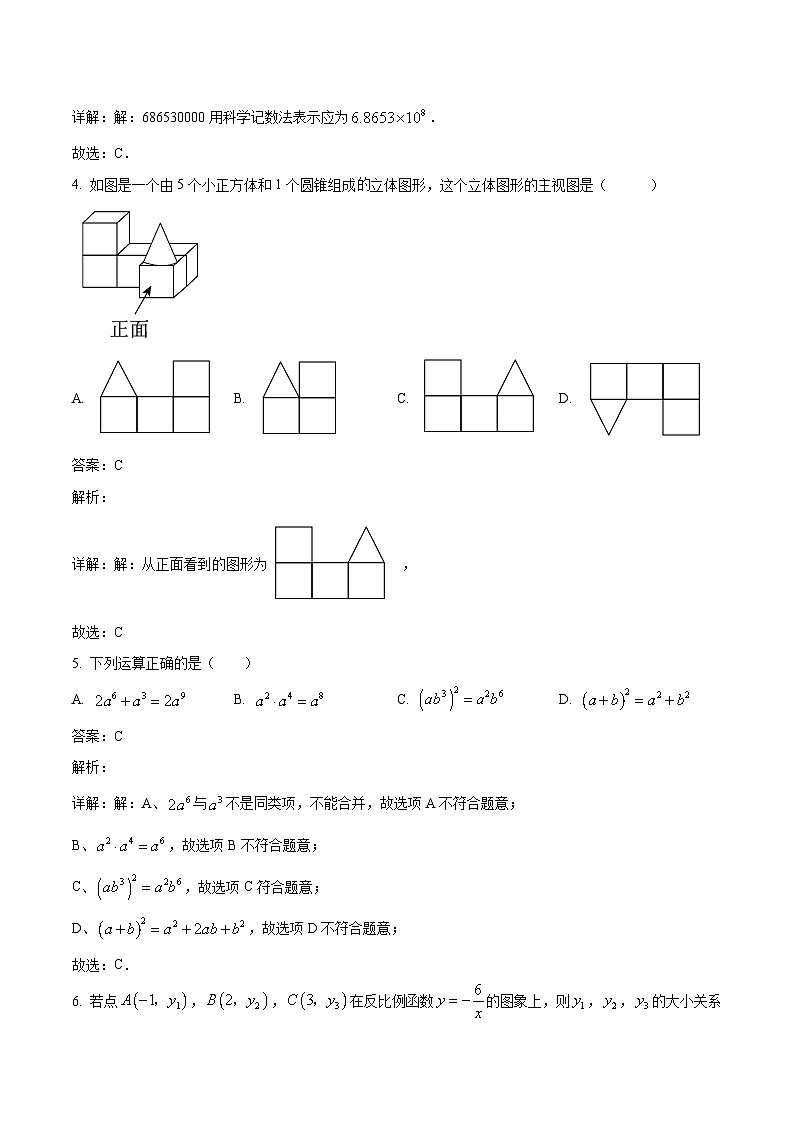
4. 如图是一个由5个小正方体和1个圆锥组成立体图形，这个立体图形的主视图是（ ）
A. B. C. D.
答案：C
解析：
详解：解：从正面看到的图形为 ，
故选：C
5. 下列运算正确的是（ ）
A. B. C. D.
答案：C
解析：
详解：解：A、与不是同类项，不能合并，故选项A不符合题意；
B、，故选项B不符合题意；
C、，故选项C符合题意；
D、，故选项D不符合题意；
故选：C．
6. 若点，，在反比例函数的图象上，则，，的大小关系是（ ）
A B. C. D.
答案：C
解析：
详解：解；∵反比例函数解析式为，，
∴反比例函数图象经过第二、四象限，在每个象限内，y随x增大而增大，
∵点，，在反比例函数的图象上，且，
∴，
故选：C．
7. 如图，点是上两点，连接并延长交切线于点，连接、、、，若，则（ ）
A. B. C. D.
答案：D
解析：
详解：解：切于，
，
，
，
，
，
，
故选：D．
8. 随着城际交通的快速发展，某次动车平均提速60，动车提速后行驶480与提速前行驶360所用的时间相同．设动车提速后的平均速度为x，则下列方程正确的是（ ）
A. B. C. D.
答案：B
解析：
详解：解：根据题意，得．
故选：B．
9. 某路灯示意图如图所示，它是轴对称图形．若，，与地面垂直且，则灯顶A到地面的高度为（ ）m
A. B. C. D.
答案：B
解析：
详解：解：如图，过点E作于点E，过点C作于点M，
所以，四边形是矩形，
∴，
∵路灯图是轴对称图形，且，
∵
在中，
又
∴，
∴
即灯顶A到地面的高度为
故选：B
10. 如图，在矩形中，O为的中点，过点O作的垂线，分别交于点F，交于点E，G是的中点，且，有下列结论：①；②；③连结，，四边形为菱形；④其中正确的是（ ）
A. ②③B. ③④C. ①②④D. ①③④
答案：D
解析：
详解：解：连接，如图，
∵G是的中点，O为的中点，
∴，故②错误，
∵，
∴，
∵，
∴，
设，则，，
在中，，
∴，，
∵矩形，
∴，，
∴，
在中，，，
∴，故①正确，
∵，，，
∴，
∴，
∵O为的中点，，
∴，，即：，
∴四边形为菱形，故③正确，
，，
∴，故④正确，
综上所述：①③④正确，
故选：D．
二、填空题（本大题共6个小题，每小题4分，共24分）
11. 若在实数范围内有意义，则x的取值范围是______．
答案：
解析：
详解：解：式子在实数范围内有意义，则，
解得：．
故答案为：．
12. 分解因式：x2－9＝______．
答案：(x＋3)(x－3)
解析：
详解：解：x2-9=（x+3）（x-3），
故答案为：（x+3）（x-3）.
13. 一组数据，它的中位数是23，则这组数据的平均数为______．
答案：
解析：
详解：解：∵一组数据，它的中位数是23，且这组数据只有5个数，
那么把这组数据从小到大排列，最中间的数为23，
∴，
∴这组数据的平均数为，
故答案为：．
14. 如图，中，，，请依据尺规作图的作图痕迹，计算______．
答案：81
解析：
详解：解：∵，，
∴，
根据作图痕迹可得AD是的平分线，
∴，
根据作图痕迹可得EF是线段BC的垂直平分线，
∴，
∴，
∴．
故答案为：81．
15. 马面裙（图1），又名“马面褶裙”，是我国古代女子穿着的主要裙式之一，如图2，马面裙可以近似地看作扇环（和的圆心为点O），A为的中点，，则该马面裙裙面（阴影部分）的面积为______．
答案：
解析：
详解：解：∵，，A为的中点，
∴为等边三角形，，
∴，
∴；
故答案为：．
16. 已知关于x的二次函数，当时，函数有最小值，则k的值为_____．
答案：1或
解析：
详解：解：∵二次函数解析式为，
∴二次函数开口向下，对称轴为直线，
∴在对称轴右侧，y随x增大而减小，在对称轴左侧，y随x增大而增大，
当时，则当时，y有最小值，
∴，
∴，
解得或，都不符合题意；
当时，则当时，y有最小值，
∴，
∴，
解得（舍去）
当时，则函数在或处取得最小值，
当时，在处取得最小值，此时或（舍去）；
当时，在处取得最小值，此时或（舍去）；
综上所述，或，
故答案为：1或．
三、解答题（本大题共86分，解答题应写出解题步骤或推理过程）
17. 计算：
答案：
解析：
详解：解：原式
18. 已知：如图，四边形是平行四边形，P，Q是对角线上的两个点，且．求证：．
答案：证明见解析
解析：
详解：证明：∵四边形是平行四边形，
∴，
∴，
在和中，
，
∴，
∴．
19. 先化简，再求值：，其中：
答案：，
解析：
详解：解：
当时，原式．
20. 《九章算术》是我国古代的数学专著，几名学生要凑钱购买1本．若每人出8元，则多了3元；若每人出7元，则少了4元．问学生人数和该书单价各是多少？
答案：学生人数为7人，该书的单价为53元．
解析：
详解：解：设学生人数为x人，由题意得：
，
解得：，
∴该书单价为（元），
答：学生人数为7人，该书的单价为53元．
21. 李白是唐朝伟大的浪漫主义诗人，被后人誉为“诗仙”．《行路难•其一》是李白不受重用，求仕无望后满怀愤慨所作的名篇．王铭和李虹将这首诗中的四句分别写在编号为，，如图所示，卡片除编号和内容外，将这4张卡片背面朝上，洗匀放好
（1）王铭从中抽取一张卡片，恰好抽到“长风破浪会有时”的概率为 ；
（2）李虹先抽一张卡片，接着王铭从剩下的卡片中抽一张，用画树状图或列表的方法求两人所抽卡片上的诗句恰好成联的概率．（注：与为一联，与为一联）
答案：（1）
（2）
解析：
小问1详解：
解：由题意得，王铭从中抽取一张卡片，恰好抽到“长风破浪会有时”的概率为，
故答案为：．
小问2详解：
解：列表如下：
共有12种等可能的结果，其中两人所抽卡片上的诗句恰好成联的结果有：，，，，共4种，
∴两人所抽卡片上的诗句恰好成联的概率为．
22. 如图，是的直径，与相交于点．过点的圆O的切线，交的延长线于点，．

（1）求的度数；
（2）若，求的半径．
答案：（1）
（2）
解析：
小问1详解：
如图，连接．

为切线，
．
，
．
，
．
，
．
小问2详解：
如图，连接，
，，
．
，
，且，
，
，即，
，
，即半径为．
23. 综合与实践
答案：任务1：图见解析，，；任务2：；任务3：此时双层部分的长度为．
解析：
详解：解：任务1：描点并作图如图所示：
根据图象可知，变量、满足一次函数关系．
设、为常数，且，
将，和，代入，
得，
解得，
．
将和代入，
得，解得；
当背带都为单层部分时，；
当背带都为双层部分时，，即，解得，
的取值范围是；
任务2：∵背带的总长度为单层部分与双层部分的长度和，
总长度为，
当单肩包背带长度调整为最佳背带总长度时，得，
；
任务3：由素材可知，当背包的背带调节到最短时都为双层部分，即，．
背包提在手上，且背包的悬挂点防地面高度为，
手到地面的距离为，即．
设小明爸爸的身高为 ．
臂展和身高一样，且肩宽为，
小明爸爸一条胳膊的长度为，
，解得，
根据任务2，得，解得，
此时双层部分的长度为．
24. 如图，在中，，点D是线段上一动点，连接，将绕点D逆时针旋转，得到．
（1）如图1，若B，E，C三点共线时，求的长；
（2）如图2，若，交AC于点F，求；
（3）如图3，连接，请直接写出的最小值．
答案：（1）
（2）
（3）CE的最小值是
解析：
小问1详解：
解：由旋转的性质可知，，
∵B，E，C三点共线，
∴，
∵，
∴，
∴，，
∴，
∴，
∴的长为．
小问2详解：
解：同理（1）可得：，
∵，
∴为等腰直角三角形，，，
∵，
∴，
∴，
又∵，
∴，
∴，
∴，
∴．
小问3详解：
解：如图3，作于，在上取点使，连接，过作于，
由（1）可知，，
由题意知，均为等腰直角三角形，
∴，，，
∴，
∵，，
∴，
∴，
∴，
∴点在过点与夹角为的直线上运动，
∴的最小值为，，
∴，
∴的最小值为．
25. 如图，抛物线经过点、两点，与y轴负半轴交于点C，且．

（1）求抛物线的解析式；
（2）如图1，连接，R为上一点，连并延长交抛物线于点T，若，求点T的坐标；
（3）如图2，点C关于抛物线对称轴的对称点为D，过点D的直线（直线不与x轴垂直）与抛物线只有一个公共点，平移直线交抛物线于E、F两点，点E在第二象限，点F在第三象限，连交y轴于点P，连交y轴于点Q，求的值．
答案：（1）
（2）或；
（3）2
解析：
小问1详解：
解：∵，，
∴，
∴，
∴，
解得：，
∴抛物线解析式为；
小问2详解：
解：设直线的解析式为，则有：
，
解得：，
∴直线的解析式为，
分别过点R、T作x轴的垂线，垂足分别为E、F，如图所示：

∴，
∴，
∵，
∴，
设，则有，
∴，
∴，
∴，
∴，
代入抛物线解析式得：，
解得：；
∴或；
小问3详解：
解：由点C关于抛物线对称轴的对称点为D，及二次函数的对称轴为直线可知点，
设直线的解析式为，则有：，
∴，
∴直线的解析式为，
联立得：，
∵直线与抛物线只有一个交点，
∴，
解得：，
∴直线的解析式为，
设直线的解析式为，
设点，联立得：，
∴根据一元二次方程根与系数的关系可得：，
设直线的解析式为，则有：
，
解得：，
∴直线的解析式为，
∴令，则有，即，
同理可得：，
∴，
∴
．生活中的数学：如何确定单肩包最佳背带长度
素材1
如图是一款单肩包，背带由双层部分、单层部分和调节扣构成．使用时可以通过调节扣加长或缩短单层部分的长度，使背带的总长度加长或缩短（总长度为单层部分与双层部分的长度和，其中调节扣的长度忽略不计）．
素材2
对于该背包的背带长度进行测量，设双层的部分长度是xcm，单层部分的长度是ycm，得到如下数据：
双层部分长度
2
6
10
14
a
单层部分长度
116
108
100
92
70
素材3
单肩包的最佳背带总长度与身高比例为2：3．
素材4
小明爸爸准备购买此款背包．爸爸自然站立，将该背包的背带调节到最短提在手上，背带在背包的悬挂点离地面的高度为；已知爸爸的臂展和身高一样，且肩宽为，头顶到肩膀的垂直高度为总身高的．
任务1
在平面直角坐标系中，以所测得数据中的x为横坐标，以y为纵坐标，描出所表示的点，并用光滑曲线连接，根据图象思考变量x、y是否满足一次函数关系．如果是，求出该函数的表达式，直接写出a值并确定x的取值范围．
任务2
设人身高为h，当单肩包背带长度调整为最佳背带总长度时，求此时人身高h与这款背包的背带双层部分的长度x之间的函数表达式
任务3
当小明爸爸的单肩包背带长度调整为最佳背带总长度时．求此时双层部分的长度．