


数学七年级上册第3章 图形的初步认识复习课件ppt
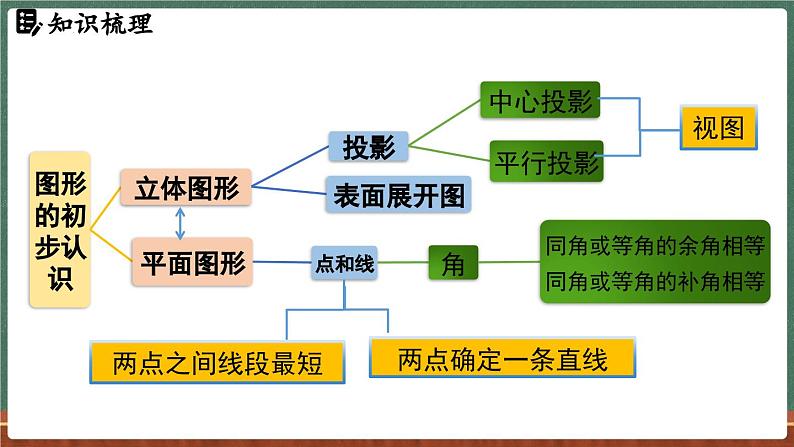
展开一、生活中的立体图形
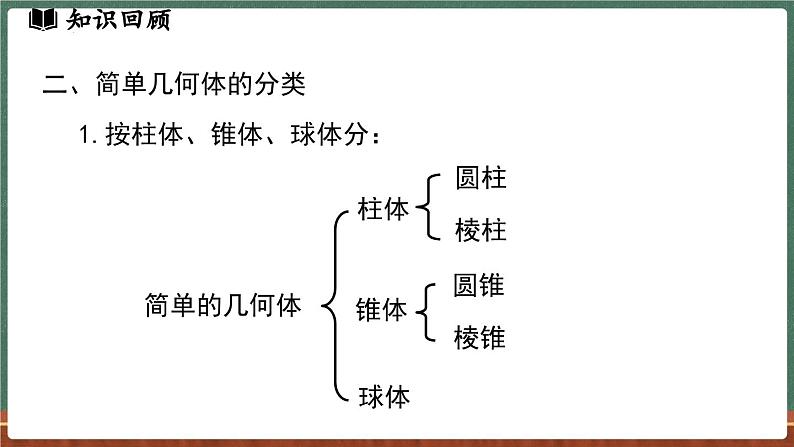
由大小相同且互相平行的两个底面(圆)和一个侧面(曲面)围成
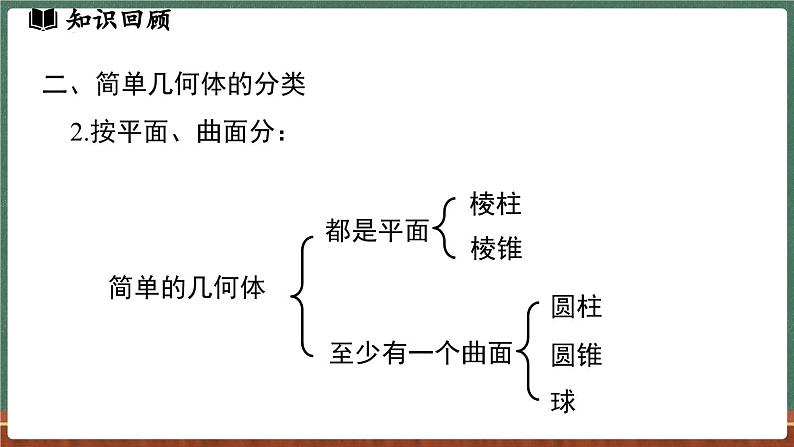
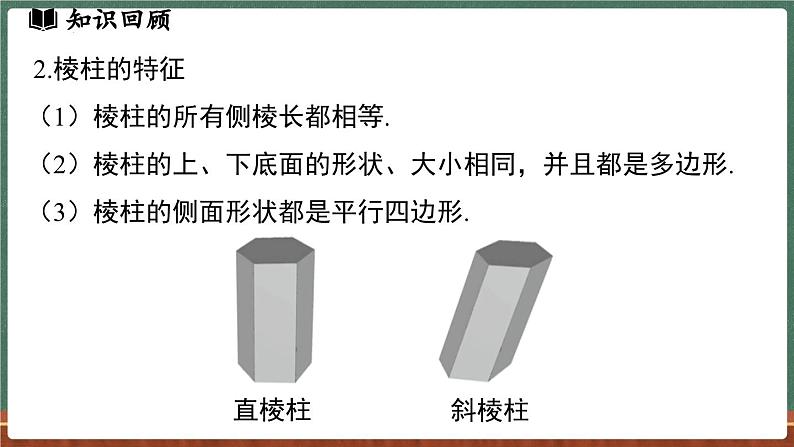
底面是多边形,侧面是长方形,n棱柱有n个侧面,有两个底面,底面互相平行且形状相同.
由一个底面(圆)和一个侧面(曲面)围成
由一个曲面围成,没有底面、侧面、顶点
1.按柱体、锥体、球体分:
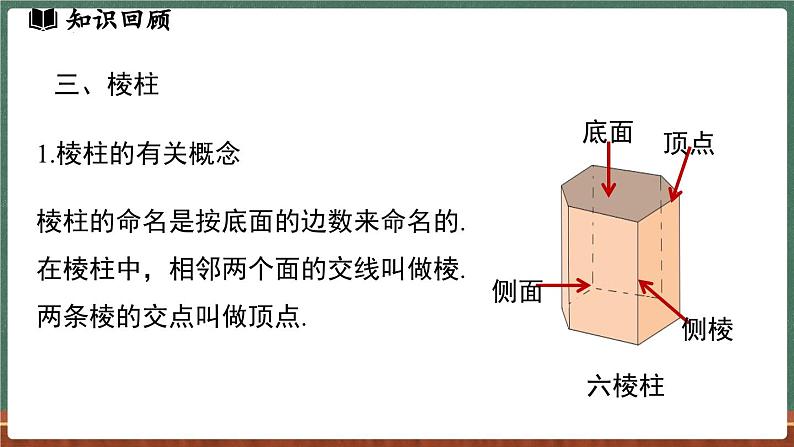
棱柱的命名是按底面的边数来命名的.在棱柱中,相邻两个面的交线叫做棱.两条棱的交点叫做顶点.
2.棱柱的特征(1)棱柱的所有侧棱长都相等.(2)棱柱的上、下底面的形状、大小相同,并且都是多边形.(3)棱柱的侧面形状都是平行四边形.
3.棱柱的顶点、棱、面:
4. n棱柱的顶点数、棱数、面数之间的关系:
n棱柱有2n个顶点,(n+2)个面,3n条棱.面数+顶点数-棱数=2
1.图形是由点、线、面构成的.
点动成线,线动成面,面动成体.
2.点、线、面、体的关系:
五、 平行投影与中心投影的区别与联系:
由平行光线形成的投影,叫做平行投影
由一点发出的光线形成的投影,叫做中心投影
都是物体在光线的照射下,在某个平面内形成的影子.
六、 三视图1.三视图的概念
2.常见几何体的三视图:
正方体展开图共有11种
正方体的表面展开图“口诀”:
一线不过四,田凹应弃之.
2.正方体的表面展开图的邻面和对面:
隔一、“Z”端是对面.
3.常见几何体的侧面及表面展开图
由线段围成的封闭图形叫做多边形.按照组成多边形的条数,多边形可分为三角形、四边形、五边形、六边形
1.线段、射线与直线的性质
线段AB或线段BA或线段a
过A,B两点作直线AB
直线AB或直线BA或直线a
以A为端点作射线AB
A,B两点有序,端点在前
经过两点有且只有一条直线.
两点之间的所有连线中,线段________ .简述为:两点之间,线段________ .
两点之间的距离是指连接两点的线段的________ .
3.比较两条线段的长短
(1)直接观察法;(2)度量法;(3)叠合法.
点M将线段AB分成_______的两条线段AM与BM,点M叫做线段AB的中点.
(1)角是由两条有公共端点的射线组成的图形.
(2)角可以看做是一条射线绕着它的端点旋转而成的图形.
一条射线绕它的端点旋转,当终边和始边成一条直线时,所成的角叫做________;终边继续旋转,当它又和始边________时,所成的角叫做周角.平角为180°,周角为360°.
(1)角的度量单位是度、分、秒.(2)它们之间的关系是六十进制的,即1°=60′,1′=60″.
借助角表示方向,通常以正北或正南为基准,配以偏西或偏东的角度来描述方向.
从一个角的顶点引出的一条射线,把这个角分成__________的角,这条射线叫作这个角的平分线.
1.下列说法错误的是( )A.长方体、正方体都是棱柱B.六棱柱有18条棱、6个侧面、12个顶点C.三棱柱的侧面是三角形D.圆柱由两个平面和一个曲面围成
2 .将下面的平面图形绕轴旋转一周,得到的立体图形是( )
A B C D
3.如图,它需再添一个面,折叠后才能围成一个正方体,下图中的黑色小正方形分别由四位同学补画,其中正确的是( )
4.如右图,是一块圆柱体形状的木头,用锯子把这个木头锯成两部分,锯开的这个面不可能是( )
5. 下图水杯的杯口与投影面平行,投影线的方向如箭头所示,它的正投影图是( )
6.下列叙述正确的是( A )
7.如图,一共有 1 条直线,是 直线AC ;能用字母表示的射线有 7 条,它们分别是射线 DA,DC,BA,BC,DB, AC ,其中在同一条直线上的射线是射线 DA,DDC , .
DA,DC,BA,BC,DB,AC,CA
DA,DC,AC,CA
8.如图所示,把一副三角板叠放在一起,则∠ACD=________°.
9.如图,∠AOB=∠COD=90° ,∠BOC=42° ,则∠AOD=( )A.48° B.148°C.138° D.128°
解析:由图可知∠AOB、∠BOC、∠COD、∠AOD组成一个周角,所以∠AOD=360°-∠AOB-∠COD-∠BOC=138°.故选C.
10.如图,线段AB=32cm,点C在AB上,且AC∶CB=5∶3,点D是AC的中点,点O是AB的中点,求DB与OC的长.
解:因为AC∶CB=5∶3,AC+CB=AB所以AC= AB= = 20 (cm),BC= AB= =12 (cm).因为D是AC的中点,所以AD= AC=10 cm,所以DB=AB-AD=32-10=22(cm).
因为O是AB的中点,所以OB= AB=16 cm,所以OC=OB-BC=16-12=4(cm),所以DB=22 cm,OC=4 cm.
11.试确定图中路灯的位置,并画出此时小赵在路灯下的影子.
12.如图,在平整的地面上,用若干个棱长完全相同的小正方体堆成一个几何体.
(1)请画出这个几何体从正面、左面、上面看到的形状图;
(2)如果现在你手中还有一些相同的小正方体,要求保持从上面和左面看到的形状图不变,最多可以再添加 个小正方体.
1.以长4 cm,宽3 cm的长方形的边所在的直线为轴,旋转一周得到一个圆柱体,则它的体积是( )
A.9π m3 B.12π m3 C.9π m3或12π m3 D.36π m3或48π m3
2.将下图所示表面带有图案的正方体沿某些棱展开后,得到的图形是( )
3.用小立方块搭一个几何体,使得它从正面看和从上面看得到的形状图,如图所示.这样的几何体只有一种吗?它最少需要多少个小立方块?最多需要多少个小立方块?
最少搭法中其中之一所需个数:3+2+1+1+1+1+1=10(个)
最多搭法时所需小立方块个数:3+3+3+2+2+2+1=16 (个)
4.如图,已知线段AB=a,点O是线段AB上的动点,且不与点A,B重合,点C,D分别是线段OA,OB的中点.(1)求线段CD的长.(2)当点O在线段AB的延长线上时,其他条件不变,请画出图形,并求出 CD的长;比较(1)(2)的结果,你发现了什么规律?
A C O D B
A C B D O
双中点线段长度计算规律(1)线段上的一点把线段分成两条线段,这两条线段的中点间的距离等于原线段长度的一半;(2)线段延长线上的一点和原线段的两个端点构成两条线段,这两条线段的中点间的距离等于原线段长度的一半.
5.探究在一条直线上n个不同的点可以构成的线段的条数.
6. 某校七年级20个班进行篮球赛,规定进行单循环赛(即每两个班比赛一场),那么该校七年级的篮球赛共要进行多少场?
7. 如图,将一张长方形纸片分别沿着EP,FP折,使点B落在点B',点C落在点C'.若点P,B',C'不在一条直线上,且两条折痕的夹角∠EPF=85°,则∠ B'PC'= .
解析:由折叠可知∠BPE=∠B'PE , ∠CPF=∠C'PF ,所以2∠B'PE+2∠C'PF-∠B'PC'=180° ,即2(∠B'PE+∠C'PF)-∠B'PC'=180° .又因为∠EPF=∠B'PE+∠C'PF-∠B'PC'=85° ,所以∠B'PE+∠C'PF=∠B'PC'+85° ,所以2(∠B'PC'+85°)-∠B'PC'=180° ,解得∠B'PC'=10° .
8.已知点O是直线AB 上一点,∠COD 是直角,OE 平分∠BOC.
(1) 如图1,若∠AOC=30°,则∠DOE 的度数为 15° ;
(2) 在图1中,若∠AOC=α,求∠DOE的度数;
初中数学沪科版(2024)七年级上册(2024)2.2 整式加减复习ppt课件: 这是一份初中数学沪科版(2024)七年级上册(2024)<a href="/sx/tb_c4053953_t3/?tag_id=26" target="_blank">2.2 整式加减复习ppt课件</a>,共21页。PPT课件主要包含了代数式,相关概念,加减运算,单项式,多项式,合并同类项,去添括号,表示数的字母,数字因数,包括前面的符号等内容,欢迎下载使用。
初中沪科版(2024)第1章 有理数复习ppt课件: 这是一份初中沪科版(2024)<a href="/sx/tb_c4053942_t3/?tag_id=26" target="_blank">第1章 有理数复习ppt课件</a>,共23页。PPT课件主要包含了有理数的基本概念,有理数的运算,有理数,相反数,20没有倒数,绝对值,有理数大小的比较,①同号相加,有理数加法法则,②异号相加等内容,欢迎下载使用。
初中数学华东师大版(2024)七年级上册1.4 绝对值课前预习ppt课件: 这是一份初中数学华东师大版(2024)七年级上册<a href="/sx/tb_c4050067_t3/?tag_id=26" target="_blank">1.4 绝对值课前预习ppt课件</a>,共15页。PPT课件主要包含了学习目标,课堂导入,绝对值的性质,例2化简,例3计算,随堂练习等内容,欢迎下载使用。













