初中数学北师大版七年级上册1.2 展开与折叠课文内容ppt课件

这是一份初中数学北师大版七年级上册1.2 展开与折叠课文内容ppt课件，共21页。PPT课件主要包含了感悟新知，课堂达标等内容，欢迎下载使用。
1.通过展开与折叠，进一步认识棱柱、圆锥和圆柱，发展空间观念．2．(2022课标)了解直棱柱、圆柱、圆锥的侧面展开图，能根据展开图想象和制作模型，培养空间想象能力．
知识点1　棱柱、圆柱、圆锥的表面展开图
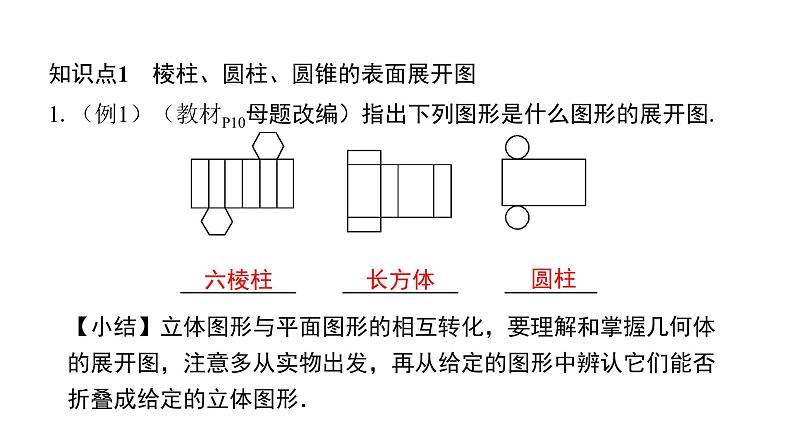
1.（例1）（教材P10母题改编）指出下列图形是什么图形的展开图.
　六棱柱　　　　长方体　　　　圆柱　
【小结】立体图形与平面图形的相互转化，要理解和掌握几何体的展开图，注意多从实物出发，再从给定的图形中辨认它们能否折叠成给定的立体图形．
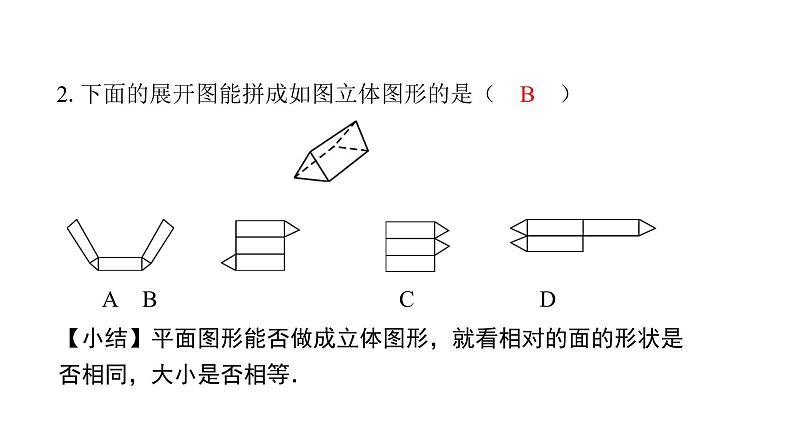
2.下面的展开图能拼成如图立体图形的是（　B　）
【小结】平面图形能否做成立体图形，就看相对的面的形状是否相同，大小是否相等．
知识点2　求立体图形的表面积
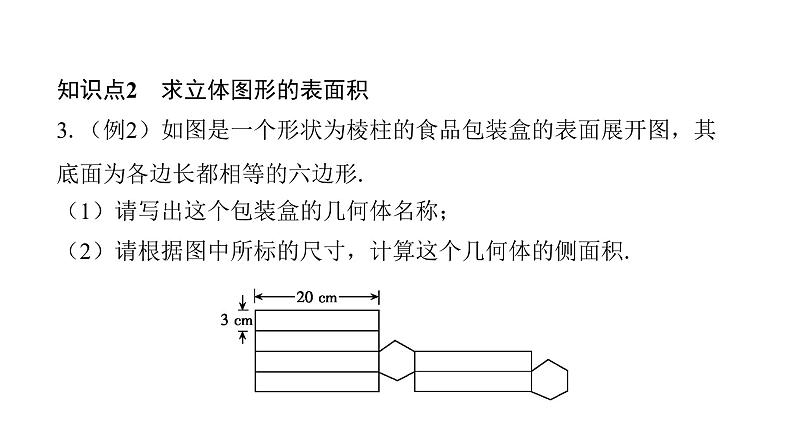
3.（例2）如图是一个形状为棱柱的食品包装盒的表面展开图，其底面为各边长都相等的六边形.
（1）请写出这个包装盒的几何体名称；
（2）请根据图中所标的尺寸，计算这个几何体的侧面积.
解：（1）这个包装盒为六棱柱.
（2）这个几何体的侧面积为6×3×20＝360（cm2）.
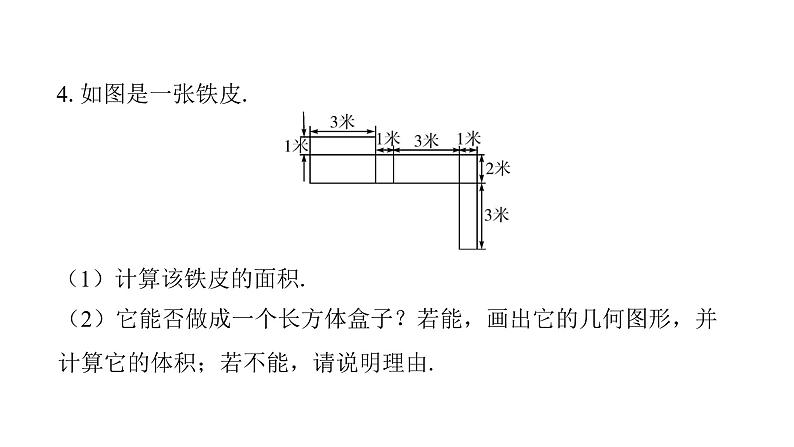
（1）计算该铁皮的面积.
（2）它能否做成一个长方体盒子？若能，画出它的几何图形，并计算它的体积；若不能，请说明理由.
解：（1）该铁皮的面积为（1×3）×2＋（2×3）×2＋（1×2）×2＝22（平方米）.
（2）能做成一个长方体盒子，如图所示.它的体积为3×1×2＝6（立方米）.
1.下列图形是三棱柱的展开图的是（　A　）
2.下列平面图形能围成一个圆锥的是（　A　）
3.下面图形不能围成一个长方体的是（　D　）
4.如图是一个长方体的展开图，每个面上都标注了字母，如果F面在前面，B面在左面（字母朝外），那么在后面的是　A面　. 
5.如图，将图中的阴影部分剪下来，围成一个几何体的侧面，使AB，DC重合，则所围成的几何图形是图中的（　D　）
A B C D
6.如图，三棱柱底面边长都是3 cm，侧棱长为5 cm，则此三棱柱共有　3　个侧面，侧面展开图的面积为　45　cm2. 
7.如图是一个几何体的平面展开图.
（1）这个几何体是　　　　　； 
（2）求这个几何体的体积.（π取3.14）
解： （2）因为圆柱的高是20 cm，底面圆的直径是10 cm，所以3.14×（10÷2）2×20＝1570（cm3）.
答：这个几何体的体积是1570 cm3.
8.[空间观念、几何直观]综合与实践如图，小明用若干个正方形和长方形拼成一个长方体的展开图.拼完后，小明觉得所拼图形似乎存在问题.
（2）若图中的正方形边长为5 cm，长方形的长为8 cm，请计算修正后所折叠而成的长方体的表面积.
解：（1）存在的问题是多余一个正方形，多余的正方形如图所示.
（2）表面积为52×2＋8×5×4＝210（cm2）.
（1）请你帮小明分析一下拼图是否存在问题，若有多余块，则把图中多余部分涂黑；若还缺少，则直接在原图中补全；