人教版八年级上册13.4课题学习 最短路径问题教学演示课件ppt

这是一份人教版八年级上册13.4课题学习 最短路径问题教学演示课件ppt，共12页。PPT课件主要包含了学习目标，学习重点，学习难点，将军饮马问题，动手探究，以此为启发，课堂练习等内容，欢迎下载使用。

能利用轴对称解决简单的最短路径问题，体会图形的变化在解决最值问题中的作用，感悟转化思想．
利用轴对称将最短路径问题转化为“两点之间，线段最短”问题．
精通数学、物理学的海伦稍加思索，利用轴对称的知识引出了这个问题．这个问题后来被称为“将军饮马问题”
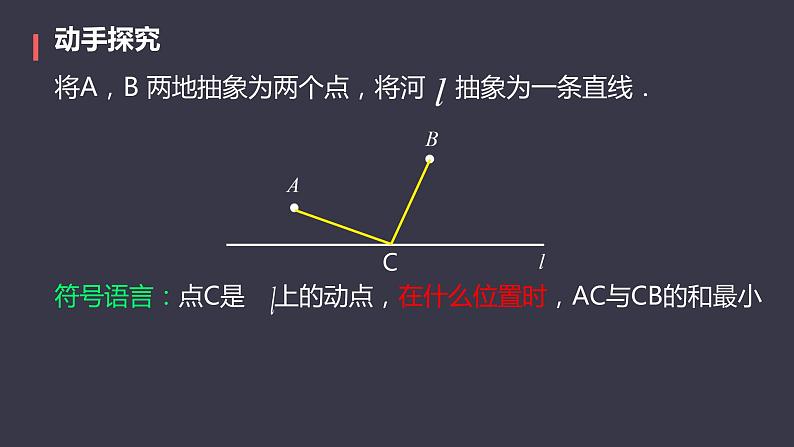
将A，B 两地抽象为两个点，将河 抽象为一条直线．
符号语言：点C是 上的动点，在什么位置时，AC与CB的和最小
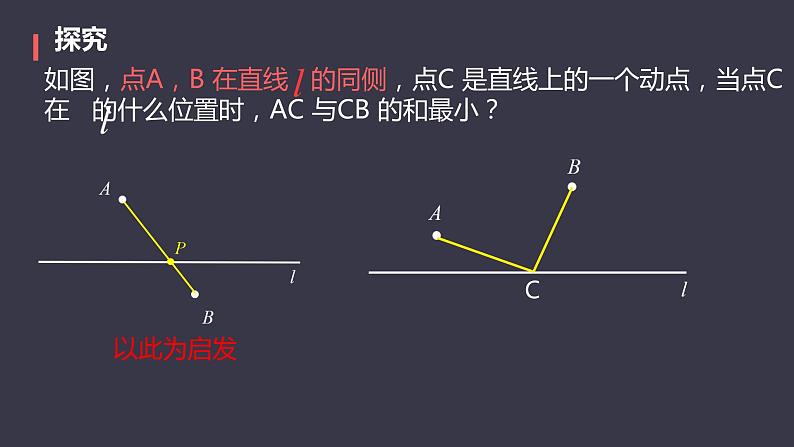
如图，点A，B 在直线 的同侧，点C 是直线上的一个动点，当点C 在 的什么位置时，AC 与CB 的和最小？
作点B 关于直线 的对称点B ′
连接AB ′，与直线 相交于点C
你能证明此时AC+BC最短吗？
证明：如图，在直线 上任取一点C ′（与点C 不重合），连接AC ′，BC ′，B ′C ′．
由轴对称性质得：BC =B ′C，BC ′=B ′C ′∴AC +BC= AC +B ′C = AB ′ AC ′+BC ′= AC ′+B ′C ′∵ AC ′+B ′C ′＞AB ′∴ AC ′+BC ′＞ AC +BC，即AC+BC最短.
如图，P，Q是△ABC的边AB，AC上的两定点，在BC上求作一点M，使△PMQ的周长最短．
提示：这本质上是“两定一动”求线段和最小的将军饮马问题．
小组讨论后展示汇报，老师做点评
将军饮马问题（视频总结）