初中26.3 解直角三角形说课课件ppt

这是一份初中26.3 解直角三角形说课课件ppt，共21页。PPT课件主要包含了解直角三角形的原则等内容，欢迎下载使用。

1.梳理、归纳直角三角形中三条边、两锐角、边角之间的关系.2.经历选择恰当的直角三角形中三边、两锐角、边角之间的关系，解直角三角形的过程.3.在探索解直角三角形的过程中,渗透数形结合思想,培养学生综合运用知识的能力.
学习重点：理解解直角三角形的概念,掌握解直角三角形的方法.学习难点：综合运用勾股定理，直角三角形的两个锐角互余及锐 角三角函数解直角三角形.
如图,轮船在A处时,灯塔B位于它的北偏东35°的方向上.轮船向东航行5 km到达C处时,轮船位于灯塔的正南方,此时轮船距灯塔多少千米?(结果保留两位小数)
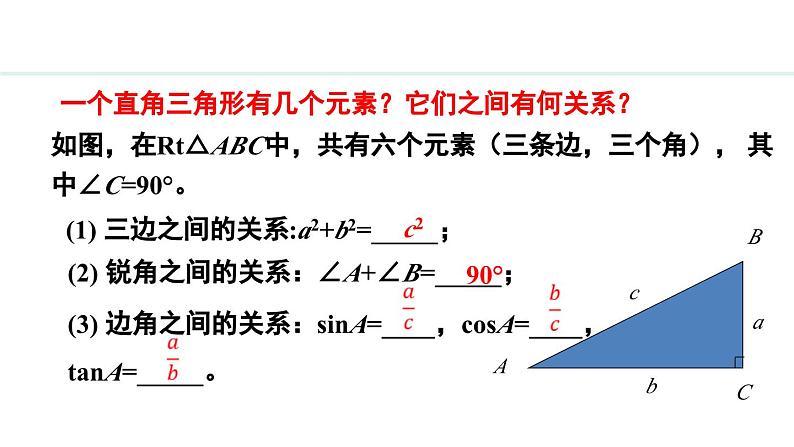
(1) 三边之间的关系:a2+b2=_____；
(2) 锐角之间的关系：∠A+∠B=_____；
(3) 边角之间的关系：sinA=____，csA=____，tanA=_____。
如图，在Rt△ABC中，共有六个元素（三条边，三个角）， 其中∠C=90°。
一个直角三角形有几个元素？它们之间有何关系？
如图所示,在RtΔABC中,∠C=90°. (1)已知直角三角形中的一个元素(除直角外), 能求其他元素吗?
在RtΔABC中,∠C=90°,若∠B=30°,你能求ΔABC的各边长吗?在RtΔABC中,∠C=90°,若AC=2,你能求ΔABC的锐角和其他边长吗?
(2)已知直角三角形中的两个元素(除直角外),有几种 可能的情况?
有三种:一边和一锐角、两边、两锐角
(3)已知直角三角形的两个元素(除直角外),能否求其他元素?
在RtΔABC中,∠C=90°,若∠B=30°,AC=2,求∠A的度数及BC, AB的长.在RtΔABC中,∠C=90°,若AC=2,AB=4,求∠A、∠B的度数和BC的长.在RtΔABC中,∠C=90°,若∠A=30°,∠B=60°,你能求出AC,BC,AB的长吗?
(4)直角三角形中已知两个元素(除直角外),可以求其他元素的情况有几种?哪几种?
解直角三角形的条件可分为两大类：（1）已知一锐角、一边（一锐角、一直角边或一锐角、一斜边）；（2）已知两边（一直角边、一斜边或两条直角边）.
【归纳总结】在直角三角形中,除直角外,还有三条边和两个锐角共五个元素.由这五个元素中的已知元素求出其余未知元素的过程,叫做解直角三角形.
例1：如图，在Rt△ABC 中，∠C=90°,∠A =34°，AC=6.解这个直角三角形.（结果精确到0.01）（sin34°≈0.60,cs34°≈0.56,tan34°≈0.67)
解：∠B=90°-∠A=90°-34°=56°. 在Rt△ABC中
∴BC=AC·tanA=6×tan34°≈6×0.6745=4.047
sin34°≈0.60,cs34°≈0.83,tan34°≈0.67
例2 如图，在Rt△ABC中，∠C=90°,AC=15，BC=8.解这个直角三角形.（角度精确到1”）
∴∠B=90°-∠A=90°-28°=62°.
在Rt△ABC中，由勾股定理得
sin28°≈0.47,cs28°≈0.88,tan28°≈0.53
1.数形结合有利于分析问题；2.选择关系式时，尽量使用原始数据，以防“累积误差”和“一错再错”；3.解直角三角形时，应求出所有未知元素.
（1）有角先求角，无角先求边
（2）有斜用弦, 无斜用切；
宁乘毋除, 取原避中。
当△ABC为锐角三角形时，如图②，BC=BD+CD=12+5=17.
当△ABC为钝角三角形时，如图①，
∵AC=13，∴由勾股定理得CD=5
∴BC=BD-CD=12-5=7；
∴BC的长为7或17.
解法：只要知道五个元素中的两个元素（至少有一个是边），就可以求出余下的三个未知元素