2023-2024学年河北省邯郸市肥乡区八年级（下）期末数学试卷（含答案）

这是一份2023-2024学年河北省邯郸市肥乡区八年级（下）期末数学试卷（含答案），共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1.将不等式−6x−3D. x10000−200x300 B. 10000−200x−200250≥10000−200x300
C. 10000−200x+200250≥10000−200x300 D. 10000−200x+200250>10000−200x300
12.如图，在△ABC中，∠ACB=90°，△ACD和△BCE均为等腰直角三角形，且面积之和为252，则AB=( )
A. 5 2
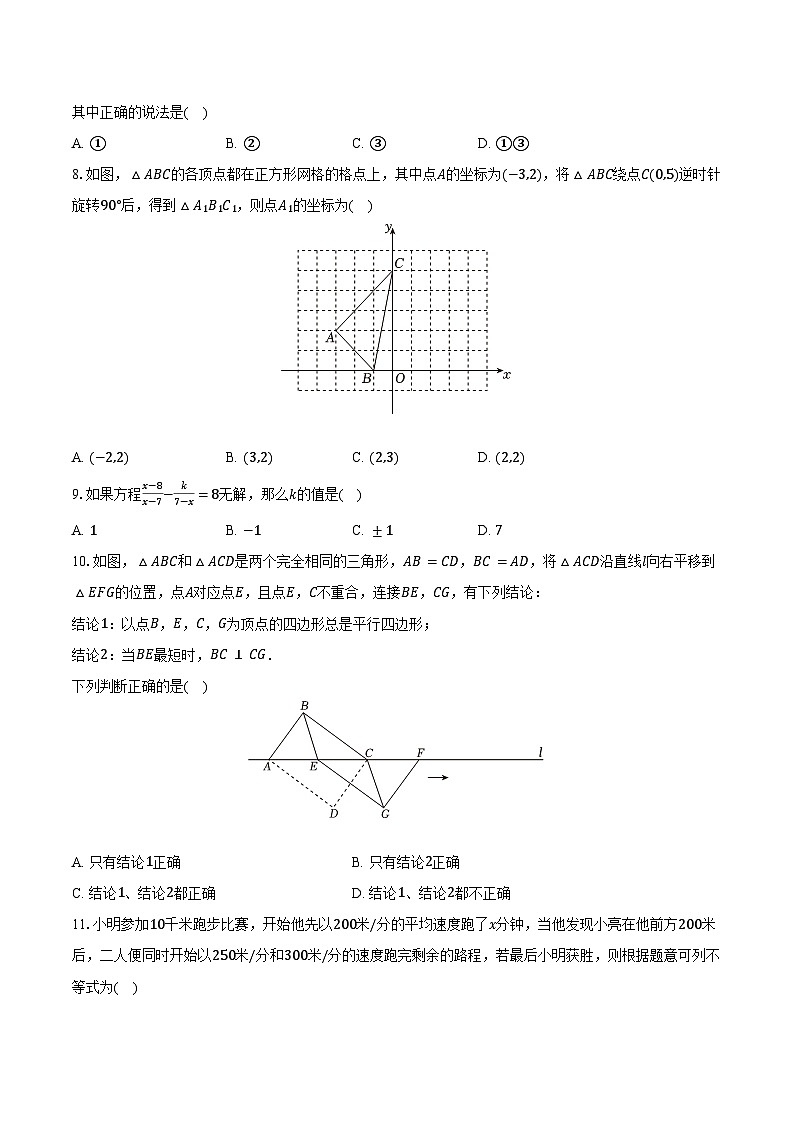
B. 25
C. 252
D. 10
二、填空题：本题共4小题，每小题3分，共12分。
13.用提公因式法分解因式4a2b3+6a3b时，应提取的公因式是______．
14.若代数式3x−4有意义，则实数x的取值范围是______．
15.把正三角形、正四边形、正五边形按如图所示的位置摆放，若∠1=52°，∠2=18°，则∠3=______．
16.如图，直线l1，y1=kx+b经过点A(4,0)，B(0,8)，点M为线段AB的中点，直线l2：y2=x+n与x轴交于点N．
(1)点M的坐标为______；
(2)当直线l2经过点M时，若y1≤y2，则x的取值范围为______；
(3)当xyy，n的取值范围为______．
三、解答题：本题共8小题，共72分。解答应写出文字说明，证明过程或演算步骤。
17.(本小题8分)
因式分解：
(1)ax4−9ay2；
(2)6xy2−9x2y−y3．
18.(本小题8分)
(1)解不等式组：5x−1>2(x+1)−x3+3≥2并将解集在数轴上表示．
(2)先化简，再求值：x2−2xx−1−11−x，其中x=2024．
19.(本小题8分)
老师布置了教材中的习题作为今天的作业：
用两种方法计算(3xx−2−xx+2)⋅x2−4x．
下面是小李同学作业中的部分运算过程：
解：原式=[3x(x+2)(x−2)(x+2)−x(x−2)(x−2)(x+2)]⋅x2−4x………………………第一步
=[3x2+6x(x−2)(x+2)−x2−2x(x−2)(x+2)]⋅(x+2)(x−2)x………第二
=3x2+6x(x2−2x)(x−2)(x+2)⋅(x+2)(x−2)x……………………………第三步
=3x2+6x−x2−2x(x−2)(x+2)⋅(x+2)(x−2)x………………………………第四步
=……
(1)以上化简步骤中，第______步是通分；
(2)第______步开始出现错误，错误的原因是______；
(3)用第二种方法化简分式．
20.(本小题8分)
如图，在△ABC中，AB=AC，AD⊥BC于点D．
(1)使用尺规作AC的垂直平分线l，交AD于点M；
(2)若BC=8，DM=6，求AM的长度．
21.(本小题8分)
【发现】一个两位数的十位上的数字为a，个位上的数字为b，a>b且a+b=10，若将其十位上的数字与个位上的数字调换位置，得到一个新的两位数，则这两个数的平方差是20的倍数．
【解决问题】
(1)用含a的代数式表示：
原来的两位数为______，新的两位数为______；
(2)使用因式分解的方法说明【发现】中的结论正确．
22.(本小题10分)
如图，在▱ABCD中，对角线AC，BD相交于点O，M，N分别为射线OB，OD上的两个动点(点M，N始终在▱ABCD的外面)，连接AM，AN，CM，CN．
(1)若DN=2OD，BM=2OB，求证：四边形AMCN为平行四边形；
(2)若DN=1nOD，BM=1nOB(n>0)
①四边形AMCN为平行四边形吗？请说明理由；
②当n=1时，S△MBC=2，直接写出四边形AMCN的面积．
23.(本小题10分)
某商场有一定数量的A，B两个款式的T恤，其中A款T恤一共花费1200元，B款T博一共花费6000元，每件B款T恤的进价比每件A款T恤的进价高80元，且B款T恤的数量刚好是A款T恤数量的3倍．
(1)求第一次购进的A，B两款T恤的进价；
(2)第一批货卖完后，商场决定再购进一定数量的B款T恤，总进货量不超过60件，商场的销售情况如下：先按标价300元卖了15件，剩余的按标价打八折进行促销，若总利润不低于3220元，求第二次可购进B款T恤多少件．
24.(本小题12分)
在△ABC和△EPQ中，∠ACB=∠Q=90°，BC=EQ=6，AC=PQ=8，且点E是AB的中点，将△EPQ绕点E旋转，QE与AC交于点M．

(1)如图1，当点M为AC的中点时，求EM的长度；
(2)如图2，若点M刚好在∠ABC的平分线上，求CM的长度；
(3)如图3，当△EPQ在AB的上方，且QE⊥AB时，求MQ的长．
参考答案
1.B
2.B
3.C
4.C
5.C
6.B
7.A
8.B
9.A
10.A
11.A
12.A
13.2a2b
14.x≠4
15.32°
16.(2,4) x≥2 n≤−1
17.解：(1)原式=a(x4−9y2)=a(x2+3y)(x2−3y)；
(2)原式=−y(9x2−6xy+y2)=−y(3x−y)2．
18.解：(1)5x−1>2(x+1)①−x3+3≥2②，
解不等式①得：x>1，
解不等式②得：x≤3，
∴原不等式组的解集为：10)，四边形AMCN为平行四边形，理由如下：
∵DN=1nOD，BM=1nOB(n>0)，OD=OB．
∴DN=BM，
∴OB+BM=OD+DN，
即OM=ON，
∵OA=OC，
∴四边形AMCN为平行四边形；
②当n=1时，DN=OD，BM=OB，
∵OB=OD，
∴DN=OD=OB=BM，
∴S△CDN=S△COD=S△COB=S△MBC=2，
∴S△CMN=4S△MBC=8，
∵四边形AMCN为平行四边形，
∴AM=CN，AN=CM，
∵MN=NM，
∴△ANM≌△CMN(SSS)，
∴S△ANM=S△CMN=8，
∴S▱AMCN=S△ANM+S△CMN=8+8=16．
23.解：(1)设第一次购进的A款T恤的进价为x元，则B款T恤的进价为(x+80)元，
由题意得：6000x+80=1200x×3，
解得：x=120，
经检验，x=120是原方程的解，且符合题意，
∴x+80=120+80=200，
答：第一次购进的A款T恤的进价为120元，B款T恤的进价为200元；
(2)设第二次可购进B款T恤m件，
由题意得：m≤60(300−200)×15+(300×0.8−200)(m−15)≥3220，
解得：58≤m≤60，
∵m为正整数，
∴m=58或59或60，
答：第二次可购进B款T恤58件或59件或60件．
24.解：(1)∵点E是AB的中点，M是AC的中点，
∴EM为△ABC的一条中位线．
∴EM=12BC=12×6=3．
(2)如图，当点M刚好在∠ABC的平分线上时，连接BM，过点M作MN⊥AB于点N．

设CM=x，则AM=8−x，
∴CM=MN=x．
又∵BM=BM，
∴Rt△BNM≌Rt△BCM(HL)，
∴BN=BC=6．
在Rt△ABC中，AB= BC2+AC2= 62+82=10，
∴AN=10−6=4，
在Rt△MNA中，MN2+AN2=AM2，
∴x2+42=(8−x)2，
解得x=3，
∴当点M刚好在∠ABC的平分线上时，CM的长为3．
(3)如图，当△EPQ在AB的上方，且QE⊥AB时，连接BM，则ME垂直平分AB，

∴BM=AM．
∵E是AB的中点，AB=10，
∴AE=12AB=5．
设AM=y，则BM=y，CM=8−y，
在Rt△BCM中，BC2+CM2=BM2，
则62+(8−y)2=y2，
解得y=254，
∴ME= AM2−AE2= (254)2−52=154，
∴MQ=EQ−ME=6−154=94．