



所属成套资源:十年(2015-2024)高考真题数学分项汇编(全国通用)
- 专题13 立体几何的空间角与空间距离及其综合应用小题综合- 十年(2015-2024)高考真题数学分项汇编(全国通用) 试卷 1 次下载
- 专题14 指数、对数、幂函数、函数图象、函数零点及函数模型的应用- 十年(2015-2024)高考真题数学分项汇编(全国通用) 试卷 1 次下载
- 专题16 导数及其应用小题综合- 十年(2015-2024)高考真题数学分项汇编(全国通用) 试卷 1 次下载
- 专题17 直线与圆小题综合- 十年(2015-2024)高考真题数学分项汇编(全国通用) 试卷 2 次下载
- 专题18 圆锥曲线(椭圆、双曲线、抛物线)小题综合- 十年(2015-2024)高考真题数学分项汇编(全国通用) 试卷 1 次下载
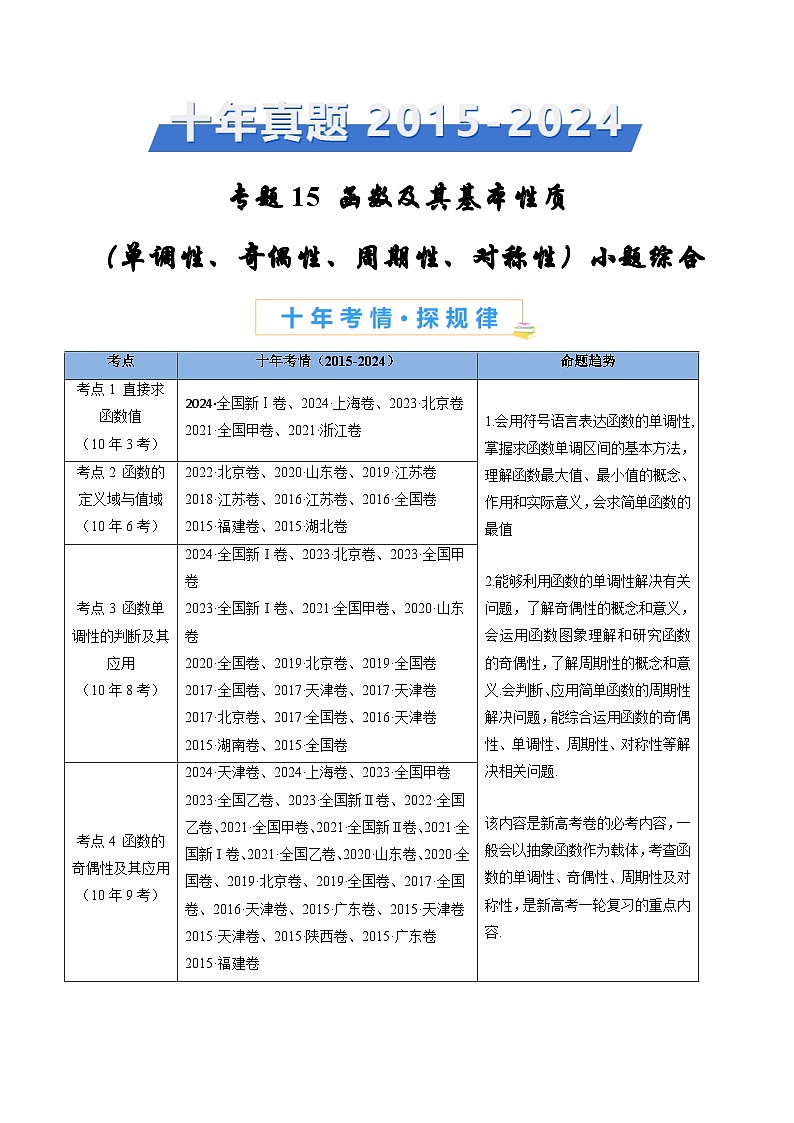
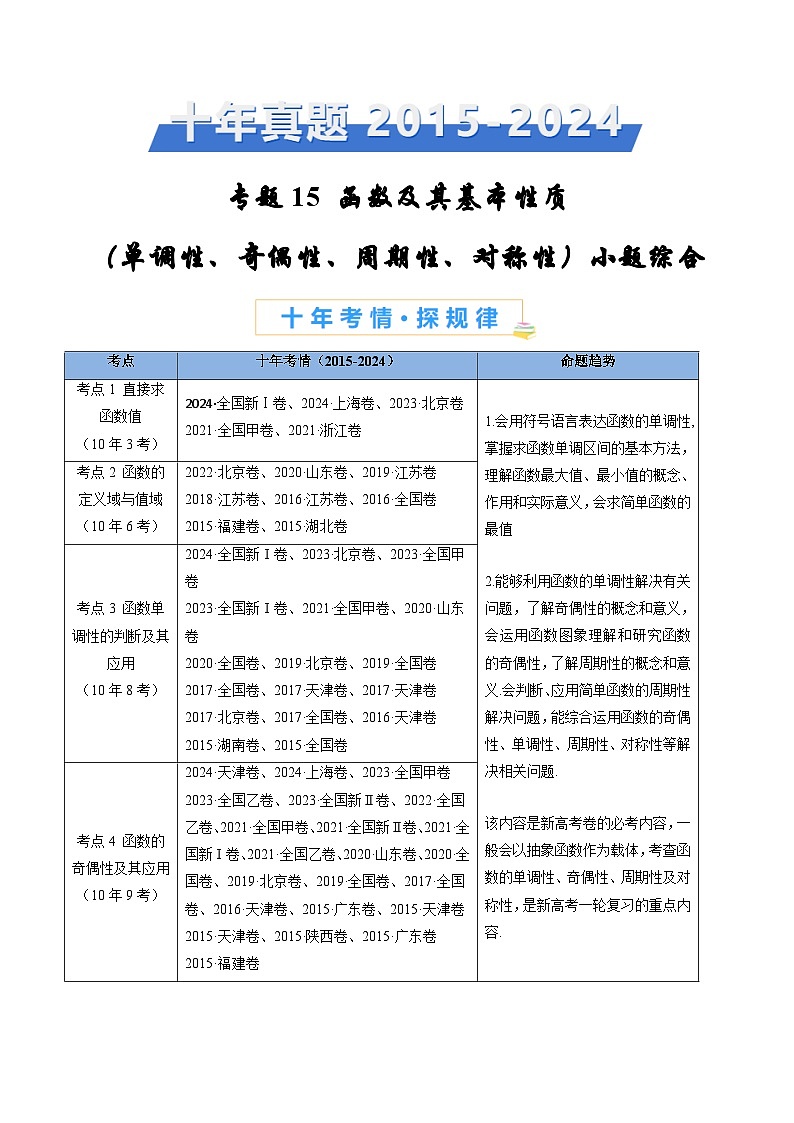
专题15 函数及其基本性质(单调性、奇偶性、周期性、对称性)小题综合- 十年(2015-2024)高考真题数学分项汇编(全国通用)
展开
这是一份专题15 函数及其基本性质(单调性、奇偶性、周期性、对称性)小题综合- 十年(2015-2024)高考真题数学分项汇编(全国通用),文件包含专题15函数及其基本性质单调性奇偶性周期性对称性小题综合教师卷-十年2015-2024高考真题数学分项汇编全国通用docx、专题15函数及其基本性质单调性奇偶性周期性对称性小题综合学生卷-十年2015-2024高考真题数学分项汇编全国通用docx等2份试卷配套教学资源,其中试卷共42页, 欢迎下载使用。
(单调性、奇偶性、周期性、对称性)小题综合
考点01 直接求函数值
1.(2024·全国新Ⅰ卷·高考真题)已知函数的定义域为R,,且当时,则下列结论中一定正确的是( )
A.B.
C.D.
2.(2024·上海·高考真题)已知则 .
3.(2023·北京·高考真题)已知函数,则 .
4.(2021·全国甲卷·高考真题)设是定义域为R的奇函数,且.若,则( )
A.B.C.D.
5.(2021·浙江·高考真题)已知,函数若,则 .
考点02 函数的定义域与值域
1.(2022·北京·高考真题)函数的定义域是 .
2.(2020·山东·高考真题)函数的定义域是( )
A.B.C.D.
3.(2019·江苏·高考真题)函数的定义域是 .
4.(2018·江苏·高考真题)函数的定义域为 .
5.(2016·江苏·高考真题)函数y=的定义域是 .
6.(2016·全国·高考真题)下列函数中,其定义域和值域分别与函数y=10lg x的定义域和值域相同的是
A.y=xB.y=lg xC.y=2xD.y=
7.(2015·福建·高考真题)若函数(且)的值域是,则实数的取值范围是 .
8.(2015·湖北·高考真题)函数的定义域为( )
A.B.
C.D.
考点03 函数单调性的判断及其应用
1.(2024·全国新Ⅰ卷·高考真题)已知函数在R上单调递增,则a的取值范围是( )
A.B.C.D.
2.(2023·北京·高考真题)下列函数中,在区间上单调递增的是( )
A.B.
C.D.
3.(2023·全国甲卷·高考真题)已知函数.记,则( )
A.B.C.D.
4.(2023·全国新Ⅰ卷·高考真题)设函数在区间上单调递减,则的取值范围是( )
A.B.
C.D.
5.(2021·全国甲卷·高考真题)下列函数中是增函数的为( )
A.B.C.D.
6.(2020·山东·高考真题)已知函数的定义域是,若对于任意两个不相等的实数,,总有成立,则函数一定是( )
A.奇函数B.偶函数C.增函数D.减函数
7.(2020·全国·高考真题)设函数,则( )
A.是奇函数,且在(0,+∞)单调递增B.是奇函数,且在(0,+∞)单调递减
C.是偶函数,且在(0,+∞)单调递增D.是偶函数,且在(0,+∞)单调递减
8.(2019·北京·高考真题)下列函数中,在区间(0,+)上单调递增的是
A.B.y=C.D.
9.(2019·全国·高考真题)设是定义域为的偶函数,且在单调递减,则
A.
B.
C.
D.
10.(2017·全国·高考真题)函数在单调递减,且为奇函数,若,则满足的的取值范围是.
A.B.C.D.
11.(2017·天津·高考真题)已知奇函数在上是增函数,若,,,则的大小关系为
A.B.C.D.
12.(2017·天津·高考真题)已知奇函数,且在上是增函数.若,,,则a,b,c的大小关系为
A.B.C.D.
13.(2017·北京·高考真题)已知函数,则
A.是奇函数,且在R上是增函数B.是偶函数,且在R上是增函数
C.是奇函数,且在R上是减函数D.是偶函数,且在R上是减函数
14.(2017·全国·高考真题)函数的单调递增区间是
A.B.
C.D.
15.(2016·天津·高考真题)已知是定义在上的偶函数,且在区间上单调递增,若实数满足,则的取值范围是
A.B.
C.D.
16.(2015·湖南·高考真题)设函数,则是
A.奇函数,且在(0,1)上是增函数B.奇函数,且在(0,1)上是减函数
C.偶函数,且在(0,1)上是增函数D.偶函数,且在(0,1)上是减函数
17.(2015·全国·高考真题)设函数,则使成立的的取值范围是
A.B.
C.D.
考点04 函数的奇偶性及其应用
1.(2024·天津·高考真题)下列函数是偶函数的是( )
A.B.C.D.
2.(2024·上海·高考真题)已知,,且是奇函数,则 .
3.(2023·全国甲卷·高考真题)若为偶函数,则 .
4.(2023·全国乙卷·高考真题)已知是偶函数,则( )
A.B.C.1D.2
5.(2023·全国新Ⅱ卷·高考真题)若为偶函数,则( ).
A.B.0C.D.1
6.(2022·全国乙卷·高考真题)若是奇函数,则 , .
7.(2021·全国甲卷·高考真题)设是定义域为R的奇函数,且.若,则( )
A.B.C.D.
8.(2021·全国新Ⅱ卷·高考真题)写出一个同时具有下列性质①②③的函数 .
①;②当时,;③是奇函数.
9.(2021·全国新Ⅰ卷·高考真题)已知函数是偶函数,则 .
10.(2021·全国乙卷·高考真题)设函数,则下列函数中为奇函数的是( )
A.B.C.D.
11.(2020·山东·高考真题)若定义在的奇函数f(x)在单调递减,且f(2)=0,则满足的x的取值范围是( )
A.B.
C.D.
12.(2020·全国·高考真题)设函数,则f(x)( )
A.是偶函数,且在单调递增B.是奇函数,且在单调递减
C.是偶函数,且在单调递增D.是奇函数,且在单调递减
13.(2019·北京·高考真题)设函数f(x)=csx+bsinx(b为常数),则“b=0”是“f(x)为偶函数”的
A.充分而不必要条件B.必要而不充分条件
C.充分必要条件D.既不充分也不必要条件
14.(2019·全国·高考真题)设f(x)为奇函数,且当x≥0时,f(x)=,则当x
相关试卷
这是一份专题13 立体几何的空间角与空间距离及其综合应用小题综合- 十年(2015-2024)高考真题数学分项汇编(全国通用),文件包含专题13立体几何的空间角与空间距离及其综合应用小题综合教师卷-十年2015-2024高考真题数学分项汇编全国通用docx、专题13立体几何的空间角与空间距离及其综合应用小题综合学生卷-十年2015-2024高考真题数学分项汇编全国通用docx等2份试卷配套教学资源,其中试卷共25页, 欢迎下载使用。
这是一份专题12 球体的外接与内切小题综合- 十年(2015-2024)高考真题数学分项汇编(全国通用),文件包含专题12球体的外接与内切小题综合教师卷-十年2015-2024高考真题数学分项汇编全国通用docx、专题12球体的外接与内切小题综合学生卷-十年2015-2024高考真题数学分项汇编全国通用docx等2份试卷配套教学资源,其中试卷共20页, 欢迎下载使用。
这是一份专题11 立体几何的基本概念、点线面位置关系及表面积、体积的计算小题综合- 十年(2015-2024)高考真题数学分项汇编(全国通用),文件包含专题11立体几何的基本概念点线面位置关系及表面积体积的计算小题综合教师卷-十年2015-2024高考真题数学分项汇编全国通用docx、专题11立体几何的基本概念点线面位置关系及表面积体积的计算小题综合学生卷-十年2015-2024高考真题数学分项汇编全国通用docx等2份试卷配套教学资源,其中试卷共52页, 欢迎下载使用。









