2024年四川省绵阳市游仙区中考模拟预测数学试题(无答案)

这是一份2024年四川省绵阳市游仙区中考模拟预测数学试题(无答案)，共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
（时间：120分钟 总分：150分）
一、选择题（本大题共12个小题，每小题3分，共36分．在每小题给出的四个选项中，只有一项是符合题目要求的．）
1．实数2的相反数是（ ）
A．－2B．2C．D．
2．下列手机中的图标是轴对称图形的是（ ）
A．B．C．D．
3．5G是第五代移动通信技术，5G网络理论下载速度可以达到每秒1300000KB以上．用科学记数法表示1300000是（ ）
A．B．C．D．
4．将一直尺和一块含30°角的三角尺按如图放置，若，则的度数为（ ）
第4题
A．40°B．50°C．130°D．140°
5．某校“啦啦操”兴趣小组共有50名学生，她们的年龄分布如表：
由于表格污损，14岁、15岁人数看不清，则下列关于年龄的统计量可以确定的是（ ）
A．平均数、众数B．众数、中位数
C．平均数、中位数D．中位数、方差
6．设，则对于实数m的范围判断正确的是（ ）
A．B．C．D．
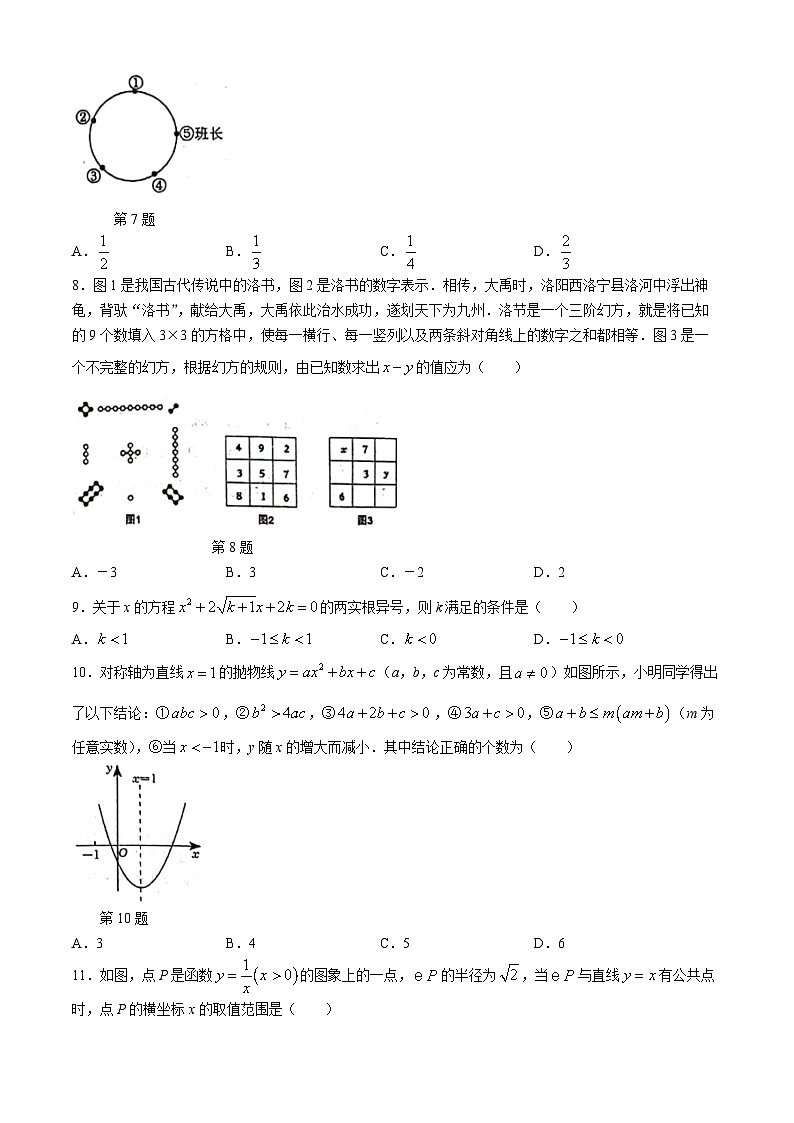
7．班长邀请A，B，C，D四位同学参加圆桌会议．如图，班长坐在⑤号座位，四位同学随机坐在①②③④四个座位，则A，B两位同学座位相邻的概率是（ ）
第7题
A．B．C．D．
8．图1是我国古代传说中的洛书，图2是洛书的数字表示．相传，大禹时，洛阳西洛宁县洛河中浮出神龟，背驮“洛书”，献给大禹，大禹依此治水成功，遂划天下为九州．洛节是一个三阶幻方，就是将已知的9个数填入3×3的方格中，使每一横行、每一竖列以及两条斜对角线上的数字之和都相等．图3是一个不完整的幻方，根据幻方的规则，由已知数求出的值应为（ ）
第8题
A．－3B．3C．－2D．2
9．关于x的方程的两实根异号，则k满足的条件是（ ）
A．B．C．D．
10．对称轴为直线的抛物线（a，b，c为常数，且）如图所示，小明同学得出了以下结论：①，②，③，④，⑤（m为任意实数），⑥当时，y随x的增大而减小．其中结论正确的个数为（ ）
第10题
A．3B．4C．5D．6
11．如图，点P是函数的图象上的一点，的半径为，当与直线有公共点时，点P的横坐标x的取值范围是（ ）
第11题
A．B．C．D．
12．如图，在矩形ABCD中，，，E为AB上一点，，P为直线CD上的动点，以PQ为斜边作，交直线AD于点Q，且满足，若F为PQ的中点，连接CE，CF，则当最小时，的值为（ ）
第12题
A．B．C．D．
二、填空题（本大题共6个小题，每小题4分，共24分，将答案填写在答题卡相应的横线上）
13．多项式，的公因式是______．
14．如图，平面直角坐标系中，点B在第一象限，点A在x轴的正半轴上，，，将绕点O逆时针旋转90°，点B的对应点的坐标是______．
第14题
15．如图，某水库堤坝横断面迎水坡AB的坡比是，堤坝高米，则迎水坡面AB的长度为______米．
第15题
16．如图，在扇形AOB中，，半径，将扇形AOB沿过点B的直线折叠，点O恰好落在上的点D处，折痕交OA于点C，则图中阴影部分的面积是______．（结果保留）
第16题
17．字母a从－2，－1，0，1，2，3这6个数中选出使关于x的不等式组有解，且使关于x的方程有唯一的解的数，a有______．
18．如图，正方形ABCD中，M、N分别是AD、BC边上的点，将四边形ABNM沿直线MN翻折，使得点A、B分别落在点、处，且点恰好为线段CD的中点，交AD于点G，作于点P，交于点Q．若，则______．
第18题
三、解答题（本大题共7个小题，共90分，解答应写出文字说明、证明过程或演算步骤）
19．（本题共2个小题，每小题8分，共16分）
（1）计算：；
（2）先化简，再求值：，其中．
20．（本题满分12分）网络直播教学是特殊时期常见的教学方式，顺德区为了解九年级教师使用线上授课软件情况，在12月份某天随机抽查了若干名老师进行调查，其中A表示“抖音直播”，B表示“腾讯会议”，C表示“腾讯课堂”，D表示“QQ群课堂”，E表示“钉钉直播”，现将调查结果绘制成两种不完整的统计图表：
请根据图表中的信息解答下列问题：
（1）______，并将频数分布直方图补充完整；
（2）已知该区共有九年级老师500人，请你估计该区使用“QQ群课堂”有多少人？
（3）该区计划在A组随机抽取两人了解使用情况，已知A组有理科老师2人，文科老师1人，请用列表法或树状图法求出抽取两名老师都是理科的概率．
21．（本题满分12分）某快递公司为了提高工作效率，计划购买A、B两种型号的机器人来搬运货物，已知每台A型机器人比每台B型机器人每天多搬运20吨，并且3台A型机器人和2台B型机器人每天共搬运货物460吨．
（1）求每台A型机器人和每台B型机器人每天分别搬运货物多少吨？
（2）每台A型机器人售价3万元，每台B型机器人售价2万元，该公司计划采购两种型号的机器人共20台，必须满足每天搬运的货物不低于1800吨，根据以上要求，设所需费用为w元，A种型号机器人的采购量为m台，当m为何值时所需费用最低？最低费用是多少？
22．（本题满分12分）已知，如图，，，G为射线BM上的一动点，AP为的角平分线且交BM于点P，以AP为边在内部作菱形APCD，使得，DP交AG于点E，连接CE并延长交AB于点F．
（1）求证：；
（2）判断CF与BM的位置关系并证明；
（3）若的周长为3，求菱形APCD的周长．
23．（本题满分12分）在平面直角坐标系中，对于不在坐标轴上的任意点，我们把点称为点A的“倒数点”．
（1）写出平面直角坐标系中第三象限内“倒数点”是本身的点的坐标______；
（2）点P是反比例函数图象上的一点，求出点P的“倒数点”Q满足的函数表达式；
（3）如图，矩形OCDE的顶点C为，顶点E在y轴上，函数的图象与DE交于点A．若点B是点A的“倒数点”，且点B在矩形OCDE的一边上，求的面积．
24．（本题满分12分）如图，内接于，BC是的直径，，过点A作，交于点E，点F是上一点，连结EF交BC于点G，连结CF交AD于点H．
（1）求证：；
（2）若，，求EF的长；
（3）设，，求y关于x的函数表达式．
25．（本题满分14分）如图，抛物线与y轴相交于点C，且经过，两点，连接AC．
（1）求抛物线的解析式；
（2）点P为抛物线在x轴下方图形上的一动点，是否存在点P，使，若存在，求出点P坐标；若不存在，说明理由；
（3）若抛物线顶点为M，对称轴与x轴的交点为N，点Q为x轴上一动点，以Q、M、N为项点的三角形与相似．请直接写出点Q坐标．年龄/岁
12
13
14
15
人数
5
23
■
■
组别
使用人数（人）
占调查人数的百分率
A
3
5%
B
12
20%
C
a
35%
D
15
c
E
b
15%