

高中数学人教A版 (2019)必修 第一册3.1 函数的概念及其表示优秀一课一练
展开一、单选题
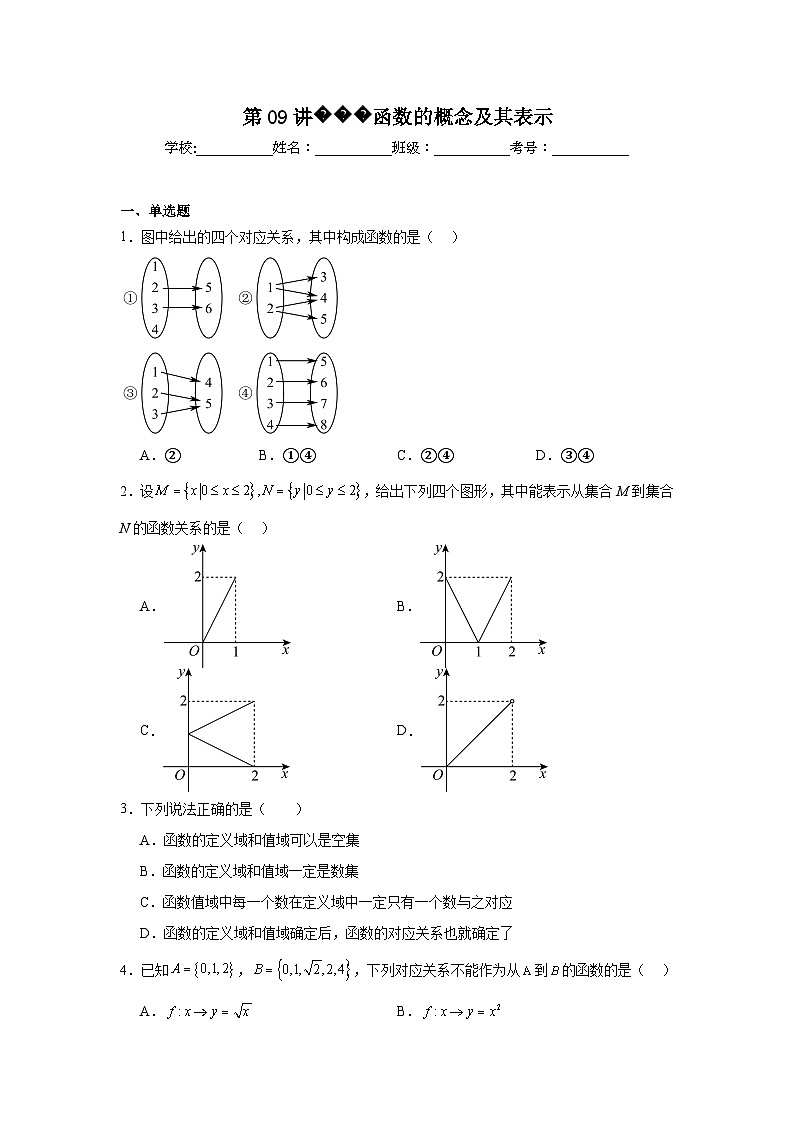
1.图中给出的四个对应关系,其中构成函数的是( )
A.②B.①④C.②④D.③④
2.设,给出下列四个图形,其中能表示从集合M到集合N的函数关系的是( )
A. B.
C. D.
3.下列说法正确的是( )
A.函数的定义域和值域可以是空集
B.函数的定义域和值域一定是数集
C.函数值域中每一个数在定义域中一定只有一个数与之对应
D.函数的定义域和值域确定后,函数的对应关系也就确定了
4.已知,,下列对应关系不能作为从到的函数的是( )
A.B.
C.D.
5.函数的定义域为( )
A.B.C.D.
6.已知函数的定义域是,则的定义域是( )
A.B.C.D.
7.若函数的定义域为,则函数的定义域为( )
A.B.C.D.
8.若函数的定义域为,则函数的定义域为( )
A.B.C.D.
9.函数,的值域是( )
A.B.C.D.
10.函数的值域为( )
A.B.C.D.
11.函数的值域是( )
A.B.C.D.
12.下列函数中,值域是的是( )
A.B.
C.D.
13.已知函数的定义域为R,则实数的取值范围是( )
A.B.
C.D.
14.若函数在区间上有意义,则实数a的可能取值是( )
A.1B.2
C.3D.4
15.若函数的定义域、值域都为,则实数满足
A.或B.
C.且D.
16.函数的定义域为,值域为,则的取值范围是
A.[0,4]B.[4,6]C.[2,6]D.[2,4]
17.已知函数,则( )
A.B.C.1D.
18.函数的定义域为,若,,则( )
A.1B.C.D.
19.已知函数,若,则a的值为( )
A.B.C.D.
20.已知函数,,下表列出了时各函数的取值,则( )
A.,B.,
C.,D.,
21.下列函数中,与函数是同一函数的是( )
A.B.
C.D.
22.下列各组函数是同一个函数的是( )
A.与B.与
C.与D.与
23.下列各组函数中,两个函数相等的是 ( )
A.与B.与
C.与D.与
24.下列四组函数中,与表示同一函数是( )
A.,B.,
C.,D.,
25.已知函数的对应关系如下表,函数的图象如下图所示,则( )
A.2B.6C.9D.0
26.小明离开家去学校上学,刚开始步行一段时间后感觉要迟到,改为跑步完成余下的路程.在下图中纵轴表示离学校的距离,横轴表示出发后的时间,则下面四个图形中较符合该学生走法的是( )
A.B.C.D.
27.已知函数的对应关系如表所示,函数的图象是如图所示,则的值为( )
A.-1B.0C.3D.4
28.中国清朝数学家李善兰在859年翻译《代数学》中首次将“functin”译做“函数”,沿用至今,为什么这么翻译,书中解释说“凡此变数中函彼变数者,则此为彼之函数”,这个解释说明了函数的内涵:只要有一个法则,使得取值范围中的每一个值x,有一个确定的y和它对应就行了,不管这个对应的法则是公式、图象、表格还是其它形式,函数由下表给出,则的值为( )
A.1B.2C.3D.4
29.二次函数的图象的顶点为,对称轴为y轴,则二次函数的解析式可以为( )
A.B.
C.D.
30.若函数,则( )
A.B.
C.D.
31.已知,则的解析式可取为( )
A.B.
C.D.
32.已知,则函数的表达式为( )
A.B.
C.D.
33.已知函数,则( )
A.2B.1C.0D.-1
34.函数的值域是( )
A.B.C.D.
35.设,若,则( )
A.14B.16C.2D.6
36.已知函数,若值域为,则实数的取值范围是( )
A.B.
C.D.
37.下列各组函数中,表示同一个函数的是( )
A.B.
C.D.
38.函数的定义域为( )
A.B.C.D.
39.函数的值域为( )
A.B.C.D.
40.设,则=( )
A.3B.5C.-1D.1
41.若函数的定义域为,值域为,那么函数的图象可能是( )
A. B.
C. D.
42.已知是定义在上的函数且,当时,,则( )
A.B.0C.4D.8
43.已知函数,若且,则它的图象可能是( )
A.B.C.D.
44.已知,则=( ).
A.B.
C.D.
二、多选题
45.已知一次函数满足,则的解析式可能为( )
A.B.C.D.
46.已知函数,则下列正确的是( )
A.B.
C.D.的值域为
三、填空题
47.函数的定义域是 .
48.已知,则函数的值域为 .
四、解答题
49.求下列函数的定义域
(1)
(2)
(3)
50.已知函数.
(1)若,求的值;
(2)求函数的值域.
51.已知函数的图象如图所示,其中y轴的左侧为一条线段,右侧为某抛物线的一段.
(1)写出函数的解析式、定义域和值域;
(2)求,的值.
52.已知函数满足,函数满足.
(1)求函数和的解析式;
(2)求函数的值域.
x
m
8
4
n
0
1
4
2
6
9
1
2
3
4
3
-1
1
2
3
参考答案:
1.D
【分析】根据函数的定义判断即可.
【详解】根据函数的定义,每个都有一个对应的唯一确定的函数值,
故只有③④符合条件.
故选:D.
2.B
【分析】逐项分析定义域和值域的对应情况,由此判断出结果.
【详解】对于A:定义域为,定义域是的真子集,故错误;
对于B:定义域为,值域为,且图像也满足函数定义,故正确;
对于C:不满足“从定义域中任意取一个有唯一的与之对应”,故错误;
对于D:定义域为,定义域是的真子集,故错误;
故选:B.
3.B
【分析】根据函数定义域和值域为非空数集可知AB正误;通过反例可说明CD错误.
【详解】对于AB,函数的定义域和值域均为非空数集,A错误,B正确;
对于C,函数中,,即值域中的数字在定义域中有两个数字与之对应,C错误;
对于D,函数与的定义域和值域均相同,但对应关系不相同,D错误.
故选:B.
4.C
【分析】根据给定条件,利用函数的定义判断即可.
【详解】对于A,对于集合的元素分别对应着中的唯一元素,A能;
对于B,对于集合的元素分别对应着中的唯一元素,B能;
对于C,对于集合的元素,在中没有元素与之对应,C不能;
对于D,对于集合的元素分别对应着中的唯一元素,D能.
故选:C
5.C
【分析】根据分母不为零且偶次方根的被开方数非负得到不等式,解得即可.
【详解】对于函数,则,解得,
所以函数的定义域为.
故选:C
6.A
【分析】根据抽象函数定义域之间的关系即可得到结论.
【详解】因为函数的定义域是,
所以,解得,
故函数的定义域是.
故选:A.
7.D
【分析】由函数定义域的概念及复合函数定义域的求解方法运算求解即可.
【详解】∵函数的定义域为,
∴要使函数有意义,
则有,解得,
∴,即函数的定义域为.
故选:D.
8.B
【分析】先求出抽象函数的定义域,然后求复合函数的定义域即可得解.
【详解】若函数的定义域为,
则,即的定义域为,
所以的定义域满足,解得
所以函数的定义域为.
故选:B.
9.D
【分析】求出函数的对称轴,结合二次函数的单调性和对称性进行求解即可.
【详解】,对称轴为,,
函数在上单调递减,在上单调递增,
,由对称性可得,
所以函数的值域是.
故选:D.
10.D
【分析】根据反比例函数的性质即可求出函数的值域.
【详解】因为,
所以,
故函数的值域为,
故选:
11.A
【分析】先求出定义域,进而根号下配方求出值域.
【详解】令得,,故定义域为,
.
故选:A
12.D
【分析】根据值域的定义结合函数解析式逐项分析判断.
【详解】对于选项A:当时,,即值域有0,故A错误;
对于选项B,因为,即值域没有1,故B错误;
对于选项C:函数的定义域为,所以函数值域不连续,故C错误.
对于选项D:因为的取值范围是,所以函数的值域为,故D正确.
故选:D.
13.A
【分析】利用题给条件列出关于的不等式,解之即可求得实数的取值范围.
【详解】由题意得对任意恒成立,
当时,不等式可化为,其解集不是R,不符合题意;
当时,由该不等式恒成立可得
,解之得,
综上,实数的取值范围是
故选:A
14.A
【分析】分,,,求出不等式的解,即可得出答案.
【详解】当时,
由可得,或,在区间上有意义,满足;
当时,
函数,显然在区间上有意义,满足题意;
当时,
由可得,或,
要使函数在区间上有意义,则应有,
所以,,所以.
综上所述,.
故选:A.
15.D
【解析】根据题意表示一次函数,可得出系数的特征,即可求出结论.
【详解】若,表示二次函数,值域不为,不合题意.
所以为一次函数,解得.
故选:D.
【点睛】本题考查一次函数、二次函数的定义域、值域,对于常用函数的性质要熟练掌握,属于基础题.
16.D
【分析】因为函数的图象开口朝上,由 ,结合二次函数的图象和性质可得的取值范围.
【详解】函数的图象是开口朝上,
且以直线为对称轴的抛物线,
故,
函数的定义域为,值域为,
所以,
即的取值范围是,故选D.
【点睛】本题主要考查二次函数的图象和性质,以及函数的定义域与值域,意在考查灵活应用所学知识解答问题的能力.
17.C
【分析】代入解析式求值即可.
【详解】由,得.
故选:C.
18.C
【分析】利用赋值法求值即可.
【详解】因为,,
所以令,得,得,
所以令,得,得.
故选:C
19.A
【分析】通过解方程求得的值.
【详解】由,得,解得.
故选:A
20.B
【分析】根据表格列出关于等式并解出,代入求出即可.
【详解】由表知,,,解得,
所以,
所以.
故选:B
21.D
【分析】根据同一函数满足定义域与解析式相同判断即可.
【详解】对A,的定义域为,的定义域为,故A错误;
对B,,故B错误;
对C,的定义域为,故C错误;
对D,,故D正确.
故选:D
22.A
【分析】根据相同函数的定义,依次判断选项即可.
【详解】A:函数和的定义域为R,解析式一样,故A符合题意;
B:函数与的定义域为R,解析式不一样,故B不符合题意;
C:函数的定义域为,的定义域为R,解析式一样,故C不符合题意;
D:函数的定义域为,的定义域为R,解析式不一样,故D不符合题意.
故选:A
23.A
【分析】判断两个函数是否相等,只需看定义域和对应法则是否都相同,由此即可逐一判断每一个选项.
【详解】对于A,与定义域都是全体实数,且,故A满足题意;
对于B,的定义域是非负实数,的定义域是全体实数,故B不满足题意;
对于C,的定义域是全体实数,的定义域是非负实数,故C不满足题意;
对于D,的定义域是全体实数,的定义域是不为0的全体实数,故D不满足题意.
故选:A.
24.D
【分析】对于ABC而言,说明两函数的定义域不同即可排除,对于D而言由绝对值的定义可以得到两函数的定义域、对应法则一样,由此即可得解.
【详解】对于A,,的定义域分别为,故A不符题意;
对于B;,的定义域分别为,故B不符题意;
对于C,,的定义域分别为,故C不符题意;
对于D,因为,其定义域、对应法则都是一样的,故D符合题意.
故选:D.
25.C
【分析】根据函数图象求得,再根据对应关系表即可求解的值.
【详解】由图可知,
由表格可知.
故选:
26.A
【分析】根据题意进行排除和判断即可.
【详解】因为纵轴表示离学校的距离,横轴表示出发后的时间,
且小明离开家去学校上学,所以纵坐标随横坐标增加而减少,故排除C和D;
由题意得,图象斜率的绝对值先小后大,故排除B.
故选:A
27.A
【分析】根据函数的定义及图表计算即可.
【详解】由图象可知,而由表格可知,所以.
故选:A
28.B
【分析】先求出,从而得到的值.
【详解】由表格可得,故.
故选:B
29.B
【分析】设出二次函数解析式,代入点,求出解析式,判断出正确答案.
【详解】由题意得,设二次函数解析式为,
将代入解析式,可得,故二次函数的解析式为,
故可以为,其他均不合要求.
故选:B
30.A
【分析】根据已知条件代入直接求解解析式即可.
【详解】因为,所以,,,.
故选:A
31.C
【分析】利用配凑法求得的解析式.
【详解】由于,
所以.
故选:C
32.C
【分析】利用配凑法先求出函数,再整体代入即可求出函数的表达式.
【详解】因为
所以
所以,即.
故选:C.
33.A
【分析】根据分段函数解析式计算可得.
【详解】因为,所以,
,
所以.
故选:A
34.C
【分析】根据题意,分别求得当时与当时,的值域,即可得到结果.
【详解】当时,,
则当时,,当时,,则;
当时,;
综上所述,.
故选:C
35.A
【分析】根据的定义域可得,分和两种情况,结合题意解得,代入求解即可.
【详解】因为的定义域为,则,解得,
若,则,可得,不合题意;
若,则,可得,解得;
综上所述:.
所以.
故选:A.
36.C
【分析】根据分段函数的解析式、的值域、的图象来求得的取值范围.
【详解】当时,,
值域为当时,由,得,
由,得,解得或,
作出的图象如下图所示,
由图象可得:,即实数的取值范围是.
故选:C.
37.A
【分析】利用同一个函数的条件是定义域相同,解析式也要相同,从而来作出判断.
【详解】选项A,解析式等价,定义域也相同,所以是同一个函数;
选项B,解析式化简后相同,但定义域不同,因为分母不能取0,所以不是同一个函数;
选项C,解析式化简后都是1,但定义域不同,因为0的0次幂没有意义,所以不是同一个函数;
选项D,解析式不同,定义域也不同,所以不是同一个函数.
故选:A.
38.D
【分析】根据二次根式和分式的意义建立不等式组,解之即可求解.
【详解】由,解得且,
所以函数的定义域为.
故选:D
39.A
【分析】化简函数,结合,求得的取值范围,即可求解.
【详解】由题意,函数(),
令,则,可得,
故()的值域为.
故选:A.
40.A
【分析】根据分段函数的定义区间和解析式,求函数值.
【详解】,则.
故选:A
41.C
【分析】根据各选项一一判断其定义域与值域,即可得解.
【详解】对于A:函数的定义域为,但是值域不是,故A错误;
对于B:函数的定义域不是,值域为,故B错误;
对于C:函数的定义域为,值域为,故C正确;
对于D:不满足函数的定义,不是一个函数的图象,故D错误.
故选:C
42.A
【分析】根据题意可得,代入运算即可.
【详解】因为,
令,可得:.
故选:A.
43.D
【分析】根据条件确定,从而抛物线开口向上,,通过排除法得出选项.
【详解】由且,得,
所以函数是二次函数,图象开口向上,排除A,C;
又,所以排除B;只有D符合.
故选:D.
44.D
【分析】利用换元法求解函数解析式,即可得答案.
【详解】令,则 ,则,
所以,
故选:D.
45.AD
【分析】根据题意,由待定系数法代入计算,即可得到结果.
【详解】设,则,
所以,解得或,
则或.
故选:AD.
46.AC
【分析】对于ABC:根据分段函数解析式运算求解;对于D通过特值可排除,即可得到答案.
【详解】对于选项A:因为,
所以,故A正确;
对于选项B,因为,所以,故B错误;
对于选项C:因为,所以,故C正确;
对于选项D:因为,故D错误;
故选:AC.
47.且
【分析】依据条件列出不等式组求解即可.
【详解】要使函数有意义,
只需,解得:且.
故答案为:且
48.
【分析】令,换元求出函数的解析式,进而可得值域.
【详解】令,则
,所以函数的值域为.
故答案为:.
49.(1)
(2)
(3)
【分析】求定义域就是求使式子有意义的实数的集合.
【详解】(1)要使分式有意义,则,
由任意,恒成立,
故函数的定义域为;
(2)要使式子各部分有意义,则,解得,且.
故的定义域为;
(3)要使分式有意义,则,
当时,,则在恒有意义;
当时,,则,无意义;
综上可知,的定义域为.
50.(1);
(2).
【分析】(1)代入解方程即可;
(2)求出二次函数最小值,再利用不等式性质求出值域即可.
【详解】(1)函数,
由,得,
即,所以.
(2)函数的定义域为R,
,当且仅当时取等号,
因此,
所以的值域为.
51.(1),定义域为,值域为;
(2),.
【分析】(1)根据图象结合待定系数法计算解析式,定义域和值域即可;
(2)直接根据(1)的结论计算即可.
【详解】(1)根据题意及图象可知:当时,可设线段解析式为,
将点代入解析式可得,即;
当时,图象为抛物线一部分,可设解析式为,
由图象可知其顶点为且过点,所以,
即,
则,
结合图象,所以的定义域为,值域为;
(2)由上可知,,
即,.
52.(1),
(2)
【分析】(1)利用换元法求出的解析式,利用解方程组法求出的解析式;
(2)利用换元法求函数的值域.
【详解】(1)令,即,所以,即,
因为①,②,
由①②解得,.
(2)因为,
令,
所以,
因为,所以,
所以该函数的值域为.
人教A版 (2019)必修 第一册1.5.1 全称量词与存在量词精品综合训练题: 这是一份人教A版 (2019)必修 第一册<a href="/sx/tb_c4053112_t7/?tag_id=28" target="_blank">1.5.1 全称量词与存在量词精品综合训练题</a>,共23页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第一册1.4.1 充分条件与必要条件精品测试题: 这是一份高中数学人教A版 (2019)必修 第一册<a href="/sx/tb_c4053110_t7/?tag_id=28" target="_blank">1.4.1 充分条件与必要条件精品测试题</a>,共19页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
必修 第一册1.3 集合的基本运算优秀课后复习题: 这是一份必修 第一册<a href="/sx/tb_c4000257_t7/?tag_id=28" target="_blank">1.3 集合的基本运算优秀课后复习题</a>,共20页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。













