第21练 函数y＝Asin(ωx＋φ)的图象性质及其应用（精练：基础+重难点）-【一轮复习讲义】2025年高考数学高频考点题型归纳与方法总结（新高考通用）

这是一份第21练 函数y＝Asin(ωx＋φ)的图象性质及其应用（精练：基础+重难点）-【一轮复习讲义】2025年高考数学高频考点题型归纳与方法总结（新高考通用），文件包含第21练函数y＝Asinωx＋φ的图象性质及其应用精练基础+重难点原卷版docx、第21练函数y＝Asinωx＋φ的图象性质及其应用精练基础+重难点解析版docx等2份试卷配套教学资源，其中试卷共64页， 欢迎下载使用。
刷真题 明导向
一、单选题
1．（2022·浙江·统考高考真题）为了得到函数的图象，只要把函数图象上所有的点（ ）
A．向左平移个单位长度B．向右平移个单位长度
C．向左平移个单位长度D．向右平移个单位长度
2．（2021·全国·统考高考真题）把函数图像上所有点的横坐标缩短到原来的倍，纵坐标不变，再把所得曲线向右平移个单位长度，得到函数的图像，则（ ）
A．B．
C．D．
3．（2022·全国·统考高考真题）将函数的图像向左平移个单位长度后得到曲线C，若C关于y轴对称，则的最小值是（ ）
A．B．C．D．
4．（2022·全国·统考高考真题）记函数的最小正周期为T．若，且的图象关于点中心对称，则（ ）
A．1B．C．D．3
5．（2023·全国·统考高考真题）已知为函数向左平移个单位所得函数，则与的交点个数为（ ）
A．1B．2C．3D．4
6．（2023·全国·统考高考真题）已知函数在区间单调递增，直线和为函数的图像的两条对称轴，则（ ）
A．B．C．D．
7．（2023·天津·统考高考真题）已知函数的一条对称轴为直线，一个周期为4，则的解析式可能为（ ）
A．B．
C．D．
二、填空题
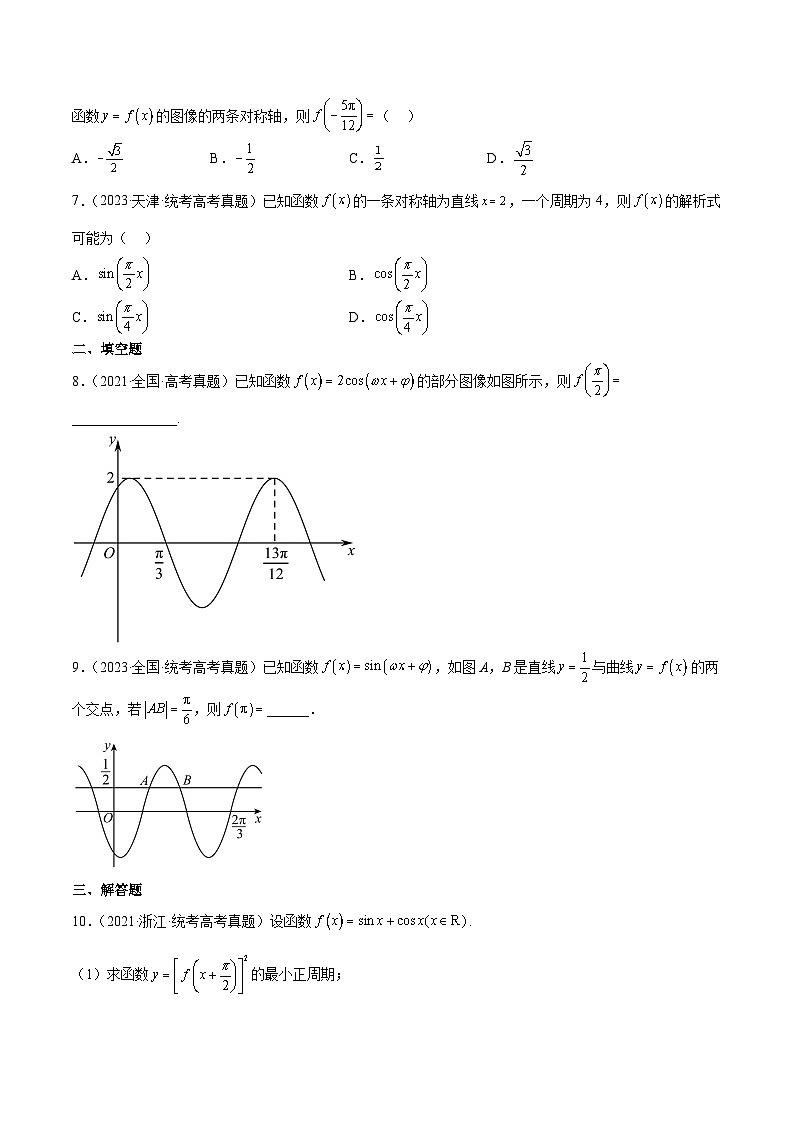
8．（2021·全国·高考真题）已知函数的部分图像如图所示，则_______________.
9．（2023·全国·统考高考真题）已知函数，如图A，B是直线与曲线的两个交点，若，则______．

三、解答题
10．（2021·浙江·统考高考真题）设函数.
（1）求函数的最小正周期；
（2）求函数在上的最大值.
【A组 在基础中考查功底】
一、单选题
1．（2023·安徽蚌埠·统考三模）已知函数，则要得到函数的图象，只需将函数的图象（ ）
A．向左平移个单位B．向右平移个单位
C．向左平移个单位D．向右平移个单位
2．（2023·河南郑州·模拟预测）把函数图象上所有点的纵坐标不变，横坐标伸长到原来的2倍，再把所得曲线向右平移个单位长度，得到函数的图象，则（ ）
A．B．
C．D．
3．（2023·福建南平·统考模拟预测）已知函数的图象的相邻两条对称轴间的距离为，则（ ）
A．的周期为
B．在上单调递增
C．的图象关于点对称
D．的图象关于直线对称
4．（2023·全国·模拟预测）将函数的图象上各点向右平移个单位长度得函数的图象，则的单调递增区间为（ ）
A．B．
C．D．
5．（2023·四川南充·统考三模）已知点是函数的一个对称中心，则为了得到函数的图像，可以将图像（ ）
A．向右平移个单位，再向上移动1个单位
B．向左平移个单位，再向上移动1个单位
C．向右平移个单位，再向下移动1个单位
D．向右平移个单位，再向下移动1个单位
6．（2023·河北石家庄·统考三模）已知函数的部分图象如图所示，则图象的一个对称中心是（ ）
A．B．C．D．
7．（2023·四川·四川省金堂中学校校联考三模）已知直线是函数图象的任意两条对称轴，且的最小值为，则的单调递增区间是（ ）
A．B．
C．D．
8．（2023·浙江绍兴·统考模拟预测）若函数的周期为，其图象由函数的图象向左平移个单位得到，则的一个单调递增区间是（ ）
A．B．
C．D．
9．（2023·四川遂宁·统考三模）已知函数，，，且的最小值为，则的值为（ ）
A．B．C．1D．2
10．（2023·山东烟台·统考二模）已知函数在上单调递增，则的取值范围为（ ）．
A．B．
C．D．
11．（2023·河北沧州·统考模拟预测）已知函数的图象关于对称，当的最小正周期取得最大值时，距离原点最近的对称中心为（ ）
A．B．C．D．
12．（2023·河南鹤壁·鹤壁高中校考模拟预测）已知函数，则下列说法正确的为（ ）
A．的最小正周期为
B．的最大值为
C．的图像关于直线对称
D．将的图像向右平移个单位长度，再向上平移个单位长度后所得图像对应的函数为奇函数
13．（2023·重庆·统考三模）将函数的图象向右平移个单位得到函数的图象，则“”是“函数为偶函数”的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
14．（2023·云南·高三校联考阶段练习）函数的部分图象如图所示，则下列叙述正确的是（ ）
A．
B．，恒成立
C．对任意
D．若，则的最小值为
二、多选题
15．（2023·全国·高三专题练习）已知函数，则（ ）
A．
B．的最小正周期为
C．把向左平移可以得到函数
D．在上单调递增
16．（2023·全国·高三专题练习）已知函数的图像关于直线对称，则ω的取值可以为（ ）
A．2B．4C．6D．8
17．（2023·云南大理·统考模拟预测）设函数在区间上单调递增，则下列说法正确的是（ ）
A．B．存在，使得函数为奇函数
C．函数的最大值为2D．存在，使得函数的图像关于点对称
18．（2023秋·江苏苏州·高三苏州中学校考阶段练习）关于函数的描述正确的是（ ）
A．图象可由的图象向左平移个单位得到
B．在单调递减
C．的图象关于直线对称
D．的图象关于点对称
三、填空题
19．（2023·福建厦门·统考二模）将函数的图象向左平移个单位长度．得到函数g(x)的图象，若g(x)是奇函数，则φ＝_______．
20．（2023·全国·高三专题练习）已知函数的图象关于点对称，那么的最小值为__________．
21．（2023春·上海闵行·高三上海市七宝中学校考阶段练习）函数的部分图象如图，若，且，则__________.
22．（2023·陕西宝鸡·校考模拟预测）已知函数在区间单调，其中为正整数，，且.则图像的一条对称轴__________.
四、解答题
23．（2023·安徽安庆·安庆一中校考三模）已知函数.
(1)求函数的单调递增区间；
(2)求在区间［0，］上的最值.
24．（2023·全国·高三专题练习）已知向量，，设
(1)求函数的最小正周期和单调递增区间；
(2)已知角为锐角，，，，求的值．
25．（2023·全国·高三专题练习）已知函数，若__________．
条件①：，且在时的最大值为；
条件②：．
请写出你选择的条件，并求函数在区间上的最大值和最小值．
注：如果选择条件①和条件②分别解答，按第一个解答计分．
【B组 在综合中考查能力】
一、单选题
1．（2023·河南·校联考模拟预测）已知函数的图象在内有且仅有一条对称轴，则的最小值为（ ）
A．0B．C．1D．
2．（2023·湖南衡阳·校考模拟预测）已知函数的导函数的图像如图所示，记，则下列说法正确的是（ ）
A．的最小正周期为2πB．
C．D．在上单调递增
3．（2023春·陕西安康·高三陕西省安康中学校考阶段练习）已知函数，若，则（ ）
A．将的图象向右平移个单位长度后，可得到一个偶函数的图象
B．图象的对称中心的坐标为
C．直线是图象的一条对称轴
D．的一个单调递增区间为
4．（2023·全国·高三专题练习）将函数的图像向右平移个单位长度，得到函数的图像，则下列说法正确的是（ ）
A．若，则是奇函数B．若，则在区间上单调递减
C．若，则的图像关于点对称D．若，则在区间上单调递增
5．（2023·全国·模拟预测）已知函数的部分图象如图所示，则下列说法正确的是（ ）

A．
B．
C．不等式的解集为
D．将的图象向右平移个单位长度后所得函数的图象在上单调递增
6．（2023·重庆·校联考三模）已知同时满足下列三个条件：
①当时，的最小值为；
②是偶函数；
③．
若在上有两个零点，则实数m的取值范围是（ ）
A．B．
C．D．
二、多选题
7．（2023·全国·高三专题练习）已知，下列结论错误的是（ ）
A．函数在区间上是减函数
B．点是函数图象的一个对称中心
C．函数的图象可以由函数的图象向左平移个单位长度得到
D．若，则的值域为
8．（2023·山东潍坊·统考二模）已知函数（其中）的部分图象如图所示，则（ ）
A．
B．函数为偶函数
C．
D．曲线在处的切线斜率为
三、填空题
9．（2023·新疆·校联考二模）已知函数满足下列条件：
①是经过图象变换得到的；
②对于，均满足成立；
③的函数图象过点．
请写出符合上述条件的一个函数解析式__________________．
10．（2023·全国·高三专题练习）将函数的图象向左平移个单位，得到函数的图象，若函数在区间上单调递增，则的取值范围______．
11．（2023·宁夏吴忠·统考模拟预测）已知函数，如图是的部分图象，则在区间上的值域是___________.
12．（2023·四川凉山·二模）已知函数，则下列说法中正确的是________
①一条对称轴为；
②将图象向右平移个单位，再向下平移1个单位得到的新函数为奇函数；
③若，则；
④若且，则的最小值为．
四、解答题
13．（2023·山东济南·统考三模）已知，其图象相邻对称轴间的距离为，若将其图象向左平移个单位得到函数的图象.
(1)求函数的解析式及图象的对称中心；
(2)在钝角中，内角的对边分别是，若，求的取值范围.
14．（2023·黑龙江齐齐哈尔·齐齐哈尔市实验中学校考三模）已知函数在区间上单调，其中，，且．
(1)求的图象的一个对称中心的坐标；
(2)若点在函数的图象上，求函数的表达式．
【C组 在创新中考查思维】
一、单选题
1．（2023·天津和平·统考二模）函数的部分图象如图所示，，则下列四个选项中正确的个数为（ ）
①
②函数在上单调递减；
③函数在上的值域为；
④曲线在处的切线斜率为．
A．0个B．1个C．2个D．3个
2．（2023春·广西防城港·高三统考阶段练习）函数，则关于函数有下列四个结论：
①的一个周期为；②的最小值为；③图像的一个对称中心为；④在区间内为增函数．
其中所有正确结论的编号为（ ）
A．①②③B．①②C．①②④D．②③
3．（2023·全国·高三专题练习）已知函数满足，若，且，则的值为（ ）
A．B．C．D．
4．（2023秋·河北石家庄·高三校联考期末）已知函数，则（ ）
A．的最小正周期是B．的图象关于直线对称
C．在上有4个极值点D．在上单调递减
二、多选题
5．（2023·重庆沙坪坝·重庆一中校考模拟预测）设函数，如图是函数及其导函数的部分图像，则（ ）

A．
B．
C．与y轴交点坐标为
D．与的所有交点中横坐标绝对值的最小值为
6．（2023·湖北·荆门市龙泉中学校联考模拟预测）已知函数在上有最大值，则（ ）
A．的取值范围为B．在区间上有零点
C．在区间上单调递减D．存在两个，使得
三、填空题
7．（2023·河北衡水·模拟预测）已知函数 ，若 ，对于任意的都有 ，且在区间 上单调，则的最大值为_________.
8．（2023·全国·高三专题练习）已知函数的部分图象如图所示，则满足条件的最小正偶数x为___________.
四、解答题
9．（2023春·重庆渝中·高三重庆巴蜀中学校考阶段练习）已知.
(1)若，求的值；
(2)将函数的图象向右平移个单位得到函数的图象，若函数在上有4个零点，求实数的取值范围.