人教A版 (2019)必修 第一册4.1 指数课前预习课件ppt

这是一份人教A版 (2019)必修 第一册4.1 指数课前预习课件ppt，共30页。PPT课件主要包含了答案C，计算下列各式的值，解析1原式，解析2原式，课堂小结，n次方根的概念，n次方根的性质，n次方根的表示，整数幂的方根，分数指数幂等内容，欢迎下载使用。
在某一适宜的环境下，某种细菌每2小时分裂一次，从一个细菌开始分裂，一个分裂成两个，经过t小时后，细菌数y为多少？
思考：这里细胞数y是时间t的函数吗？
类似地，(±2)4=16，则±2叫做16的 4次方根　； 25=32，则2叫做32的 5次方根 .
① (±2)2＝４，则称±２为４的　平方根　； ② 23=8，则称２为8的　立方根　；
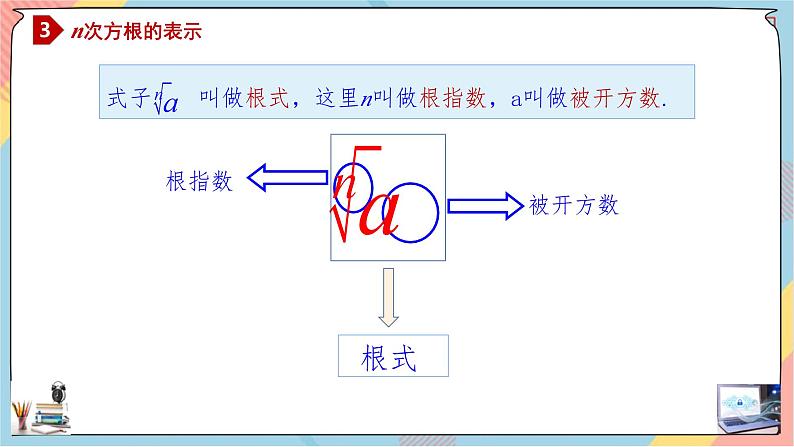
　　一般地，如果xn＝a，那么x叫做a的 ， 其中n＞1，且n∈N﹡.
(1) －32的五次方根等于_____.(2)81的四次方根等于____.(3)0的七次方根等于_____.
答案： (1)-2; (2)±3; (3)0
思考：什么情况下有正负两个方根？
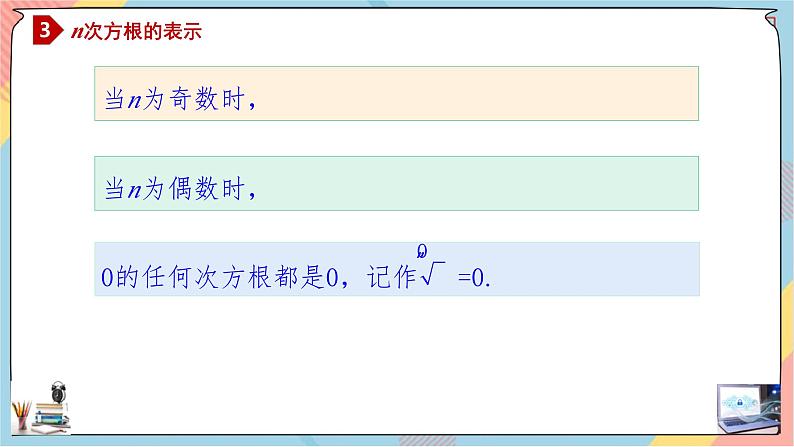
正数的奇次方根是一个正数；负数的奇次方根是一个负数；0的奇次方根是0.
正数的偶次方根有两个，且互为相反数；负数没有偶次方根；0的偶次方根是0.
0的任何次方根都是0，记作 =0.
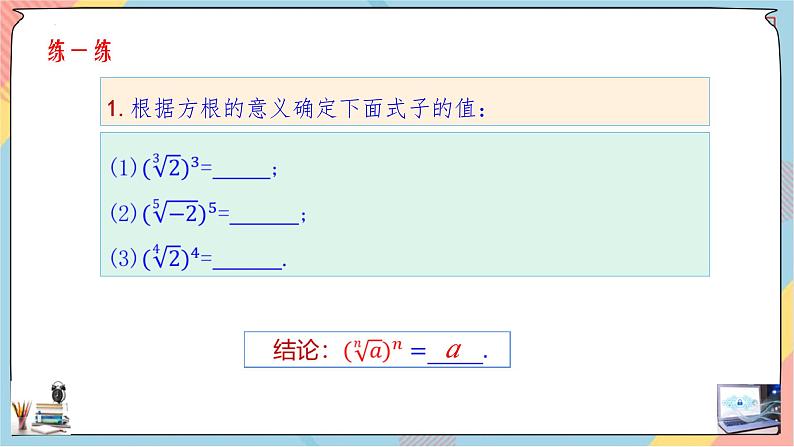
1.根据方根的意义确定下面式子的值：
⑴当n为任意正整数时，( )n = a .
⑵当n为奇数时， =a；　当n为偶数时， =|a|= .
答案：(1) -8 (2) 10 (3) π-3 (4) a - b
0的正分数指数幂等于0，0的负分数指数幂没有意义．
把下列的分数指数式化为根式，把根式化成分数指数式.
答案：（1） ； （2） ； （3） ； （4） .
解决根式的化简或求值问题,首先要分清根式为奇次根式还是偶次根式,然后运用根式的性质进行化简或求值.
有理数指数幂的运算性质
例1. 用分数指数幂的形式表示下列各式(a>0):
用分数指数幂表示下列各式：
方法总结：注意把数转化成乘方的形式.
例3. 计算下列各式(式中字母都是正数):
一、本节课学习的新知识
有理数指数幂的运算性质
二、本节课提升的核心素养
三、本节课训练的数学思想方法
基础作业： .
能力作业： .