第31练 基本立体图形及几何体的表面积与体积（精练）-【一轮复习讲义】高考数学高频考点题型归纳与方法总结（新高考通用）

这是一份第31练 基本立体图形及几何体的表面积与体积（精练）-【一轮复习讲义】高考数学高频考点题型归纳与方法总结（新高考通用），文件包含第31练基本立体几何图形及几何体的表面积与体积精练基础+重难点原卷版docx、第31练基本立体几何图形及几何体的表面积与体积精练基础+重难点解析版docx等2份试卷配套教学资源，其中试卷共106页， 欢迎下载使用。
刷真题 明导向
一、单选题
1．（2023·全国·统考高考真题）在三棱锥中，是边长为2的等边三角形，，则该棱锥的体积为（ ）
A．1B．C．2D．3
2．（2023·全国·统考高考真题）已知圆锥PO的底面半径为，O为底面圆心，PA，PB为圆锥的母线，，若的面积等于，则该圆锥的体积为（ ）
A．B．C．D．
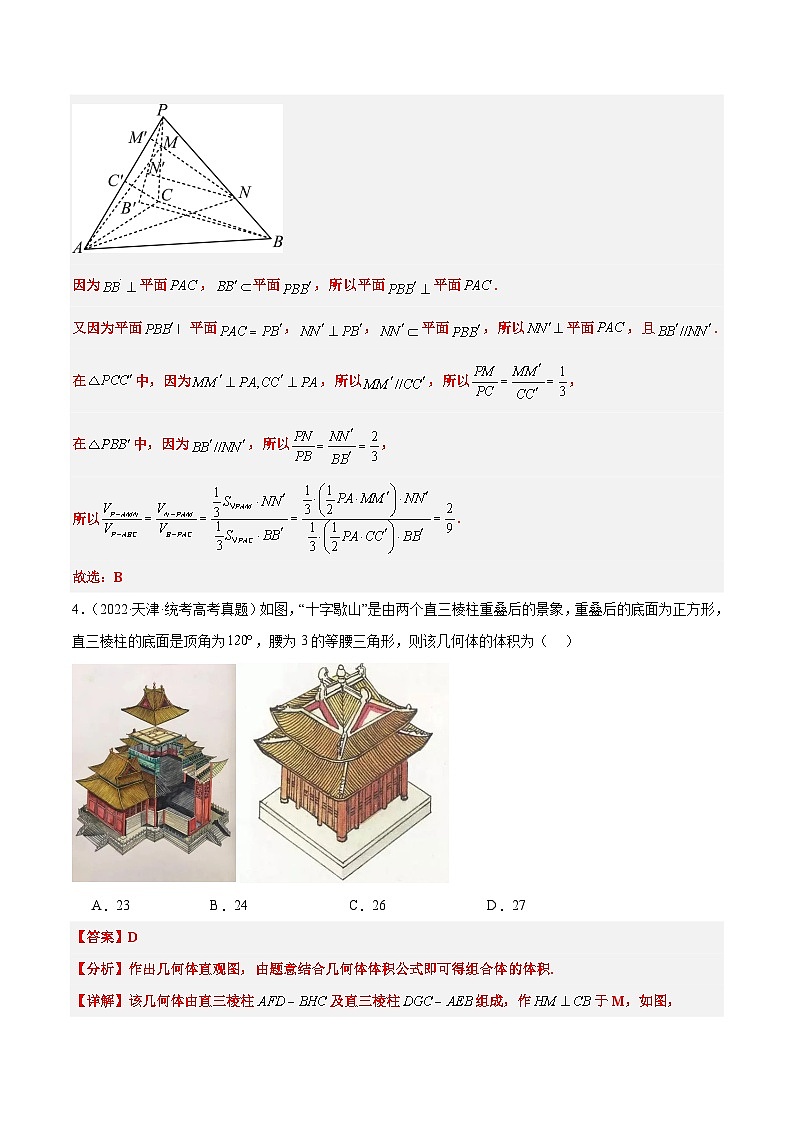
3．（2023·天津·统考高考真题）在三棱锥中，线段上的点满足，线段上的点满足，则三棱锥和三棱锥的体积之比为（ ）
A．B．C．D．
4．（2022·天津·统考高考真题）如图，“十字歇山”是由两个直三棱柱重叠后的景象，重叠后的底面为正方形，直三棱柱的底面是顶角为，腰为3的等腰三角形，则该几何体的体积为（ ）
A．23B．24C．26D．27
5．（2022·全国·统考高考真题）甲、乙两个圆锥的母线长相等，侧面展开图的圆心角之和为，侧面积分别为和，体积分别为和．若，则（ ）
A．B．C．D．
6．（2022·北京·统考高考真题）已知正三棱锥的六条棱长均为6，S是及其内部的点构成的集合．设集合，则T表示的区域的面积为（ ）
A．B．C．D．
7．（2021·天津·统考高考真题）两个圆锥的底面是一个球的同一截面，顶点均在球面上，若球的体积为，两个圆锥的高之比为，则这两个圆锥的体积之和为（ ）
A．B．C．D．
8．（2021·全国·统考高考真题）正四棱台的上､下底面的边长分别为2，4，侧棱长为2，则其体积为（ ）
A．B．C．D．
9．（2021·全国·统考高考真题）北斗三号全球卫星导航系统是我国航天事业的重要成果．在卫星导航系统中，地球静止同步卫星的轨道位于地球赤道所在平面，轨道高度为（轨道高度是指卫星到地球表面的距离）．将地球看作是一个球心为O，半径r为的球，其上点A的纬度是指与赤道平面所成角的度数．地球表面上能直接观测到一颗地球静止同步轨道卫星点的纬度最大值为，记卫星信号覆盖地球表面的表面积为（单位：），则S占地球表面积的百分比约为（ ）
A．26%B．34%C．42%D．50%
10．（2021·北京·统考高考真题）某一时间段内，从天空降落到地面上的雨水，未经蒸发、渗漏、流失而在水平面上积聚的深度，称为这个时段的降雨量（单位：）．24h降雨量的等级划分如下：

在综合实践活动中，某小组自制了一个底面直径为200 mm，高为300 mm的圆锥形雨量器.若一次降雨过程中，该雨量器收集的24h的雨水高度是150 mm（如图所示)，则这24h降雨量的等级是
A．小雨B．中雨C．大雨D．暴雨
11．（2021·全国·统考高考真题）已知圆锥的底面半径为，其侧面展开图为一个半圆，则该圆锥的母线长为（ ）
A．B．C．D．
二、多选题
12．（2022·全国·统考高考真题）如图，四边形为正方形，平面，，记三棱锥，，的体积分别为，则（ ）
A．B．
C．D．
三、填空题
13．（2021·全国·高考真题）已知一个圆锥的底面半径为6，其体积为则该圆锥的侧面积为 .
14．（2023·全国·统考高考真题）在正四棱台中，，则该棱台的体积为 ．
15．（2023·全国·统考高考真题）底面边长为4的正四棱锥被平行于其底面的平面所截，截去一个底面边长为2，高为3的正四棱锥，所得棱台的体积为 ．
【A组 在基础中考查功底】
一、单选题
1．（2023·全国·高三专题练习）已知某圆锥的高为，体积为，则该圆锥的侧面积为（ ）
A．B．C．D．
2．（2023·宁夏银川·银川一中校考三模）灯罩的更新换代比较快，而且灯具大部分都是设计师精心设计，对于灯来说，不用将灯整个都换掉，只需要把灯具的外部灯罩进行替换就可以改变灯的风格.杰斯决定更换卧室内的两个灯罩来换换氛围，已知该灯罩呈圆台结构，上下底皆挖空，上底半径为10，下底半径为18，母线长为17，侧面计划选用丝绸材质布料制作，若不计做工布料的浪费，则更换两个灯罩需要的丝绸材质布料面积为（ ）
A．B．C．D．
3．（2023·全国·高三专题练习）如图，将一个圆柱等分切割，再将其重新组合成一个与圆柱等底等高的几何体，越大，重新组合成的几何体就越接近一个“长方体”．若新几何体的表面积比原圆柱的表面积增加了10，则圆柱的侧面积为（ ）
A．B．C．D．
4．（2023春·重庆沙坪坝·高三重庆八中校考开学考试）石碾子是我国传统粮食加工工具，如图是石碾子的实物图，石碾子主要由碾盘、碾滚（圆柱形）和碾架组成．碾盘中心设竖轴（碾柱），连碾架，架中装碾滚，以人推或畜拉的方式，通过碾滚在碾盘上的滚动达到碾轧加工粮食作物的目的．若推动拉杆绕碾盘转动2周，碾滚的外边缘恰好滚动了5圈，碾滚与碾柱间的距离忽略不计，则该圆柱形碾滚的高与其底面圆的直径之比约为（ ）
A．3：2B．5：4C．5：3D．4：3
5．（2023·江西鹰潭·贵溪市实验中学校考模拟预测）转子发动机采用三角转子旋转运动来控制压缩和排放．如图，三角转子的外形是有三条侧棱的曲面棱柱，且侧棱垂直于底面，底面是以正三角形的三个顶点为圆心，正三角形的边长为半径画圆构成的曲面三角形，正三角形的顶点称为曲面三角形的顶点，侧棱长为曲面棱柱的高，记该曲面棱柱的底面积为S，高为h，已知曲面棱柱的体积，若，，则曲面棱柱的体积为（ ）
A．B．
C．D．
6．（2023·全国·高三专题练习）《九章算术·商功》中记载：“斜解立方，得两堑堵.斜解堑堵，其一为阳马，一为鳖臑，不易之率也.”我们可以翻译为：取一长方体，分成两个一模一样的直三棱柱，称为堑堵.再沿堑堵的一顶点与相对的棱剖开，得一个四棱锥和一个三棱锥，这个四棱锥称为阳马，这个三棱锥称为鳖臑.现已知某个鳖臑的体积是1，则原长方体的体积是（ ）
A．8B．6C．4D．3
7．（2023春·宁夏银川·高三宁夏育才中学校考开学考试）已知侧棱长为的正四棱锥各顶点都在同一球面上．若该球的表面积为，则该正四棱锥的体积为（ ）
A．B．C．D．
8．（2023春·湖南长沙·高三校联考阶段练习）为了给热爱朗读的师生提供一个安静独立的环境，某学校修建了若干“朗读亭”.如图所示，该朗读亭的外形是一个正六棱柱和正六棱锥的组合体，正六棱柱两条相对侧棱所在的轴截面为正方形，若正六棱锥的高与底面边长的比为，则正六棱锥与正六棱柱的侧面积的比值为（ ）
A．B．C．D．
9．（2023·云南·高三校联考阶段练习）拟柱体（所有顶点均在两个平行平面内的多面体）可以用辛普森（Simpsn）公式求体积，其中h是高，是上底面面积，是下底面面积，是中截面（到上、下底面距离相等的截面）面积，如图所示，在五面体ABCDEF中，底面ABCD是边长为4的正方形，，且直线EF到底面ABCD的距离为3，则该五面体的体积为（ ）
A．18B．20C．24D．25
10．（2023·全国·校联考三模）如图为一个火箭的整流罩的简单模型的轴截面，整流罩是空心的，无下底面，由两个部分组成，上部分近似为圆锥，下部分为圆柱，则该整流罩的外表面的面积约为（ ）
A．B．
C．D．
11．（2023·北京通州·统考模拟预测）如图，某几何体的上半部分是长方体，下半部分是正四棱锥，，，，则该几何体的体积为（ ）
A．B．C．D．
12．（2023·全国·高三专题练习）黄地绿彩云龙纹盘是收藏于中国国家博物馆的一件明代国宝级瓷器.该龙纹盘敞口，弧壁，广底，圈足.器内施白釉，外壁以黄釉为地，刻云龙纹并填绿彩，美不胜收.黄地绿彩云龙纹盘可近似看作是圆台和圆柱的组合体，其口径22.5cm，足径14.4cm，高3.8cm，其中底部圆柱高0.8cm，则黄地绿彩云龙纹盘的侧面积约为（ ）（附：圆台的侧面积，，为两底面半径，为母线长，其中的值取3，）
A．B．C．D．
13．（2023·湖南·湖南师大附中校联考模拟预测）如图所示，一个球内接圆台，已知圆台上､下底面的半径分别为3和4，球的表面积为，则该圆台的体积为（ ）
A．B．C．D．
14．（2023·全国·高三专题练习）正多面体共有5种，统称为柏拉图体，它们分别是正四面体、正六面体（即正方体）、正八面体、正十二面体、正二十面体．若连接某正方体的相邻面的中心，就可以得到一个正八面体，已知该正八面体的体积为36，则生成它的正方体的棱长为（ ）
A．8B．6C．4D．3
15．（2023·全国·高三专题练习）如图①，“球缺”是指一个球被平面所截后剩下的部分，截得的圆面叫做球缺的底，垂直于截面的直径被截得的一段叫做球缺的高.已知球缺的体积公式为，其中是球的半径，是球缺的高.某航空制造公司研发一种新的机械插件，其左右两部分为圆柱，中间为球切除两个相同的“球缺”剩余的部分，制作尺寸如图②所示（单位：cm）.则该机械插件中间部分的体积约为（）（ ）
A．B．
C．D．
二、多选题
16．（2023·全国·高三专题练习）用平行于棱锥底面的平面去截棱锥，得到上、下两部分空间图形且上、下两部分的高之比为，则关于上、下两空间图形的说法正确的是（ ）
A．侧面积之比为B．侧面积之比为
C．体积之比为D．体积之比为
17．（2023·全国·高三专题练习）“阿基米德多面体”也称为半正多面体（semi-regularslid），是由边数不全相同的正多边形为面围成的多面体，它体现了数学的对称美.如图所示，将正方体沿交于一顶点的三条棱的中点截去一个三棱锥，共可截去八个三棱锥，得到八个面为正三角形、六个面为正方形的一种半正多面体，已知，则关于如图半正多面体的下列说法中，正确的有（ ）
A．该半正多面体的体积为
B．该半正多面体过A，B，C三点的截面面积为
C．该半正多面体外接球的表面积为
D．该半正多面体的顶点数V、面数F、棱数E满足关系式
18．（2023·重庆·二模）“端午节”为中国国家法定节假日之一，已被列入世界非物质文化遗产名录，吃粽子便是端午节食俗之一．全国各地的粽子包法各有不同．如图，粽子可包成棱长为的正四面体状的三角粽，也可做成底面半径为，高为（不含外壳）的圆柱状竹筒粽．现有两碗馅料，若一个碗的容积等于半径为的半球的体积，则（ ）（参考数据：）

A．这两碗馅料最多可包三角粽35个
B．这两碗馅料最多可包三角粽36个
C．这两碗馅料最多可包竹筒粽21个
D．这两碗馅料最多可包竹筒粽20个
19．（2023·全国·高三专题练习）已知某圆锥的母线长为，其轴截面为直角三角形，则下列关于该圆锥的说法中正确的有（ ）
A．圆锥的体积为
B．圆锥的表面积为
C．圆锥的侧面展开图是圆心角为的扇形
D．圆锥的内切球表面积为
20．（2023·全国·高三专题练习）《九章算术》是中国古代张苍､耿寿昌所撰写的一部数学专著，是《算经十书》中最重要的一部，其中将有三条棱互相平行且有一个面为梯形的五面体称之为“羡除”，则（ ）
A．“羡除”有且仅有两个面为三角形；B．“羡除”一定不是台体；
C．不存在有两个面为平行四边形的“羡除”；D．“羡除”至多有两个面为梯形.
三、填空题
21．（2023·全国·高三专题练习）若圆锥的轴截面是边长为1的正三角形，则圆锥的侧面积是 .（结果用含的式子表示）
22．（2023·上海·高三专题练习）已知圆柱的底面直径和高都等于球的直径，圆柱的体积为，则球的表面积为 ．
23．（2023·全国·高三专题练习）若长方体的对角线的长为，其长、宽、高的和是，则长方体的全面积是 ．
24．（2023·全国·高三专题练习）《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有委米依垣内角，下周八尺，高五尺，问：积及为米几何？”其意思为：“在屋内墙角处堆放米（如图，米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺，米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1.62立方尺，圆周率约为3，则堆放的米约有 斛（结果精确到个位）．
25．（2023·全国·高三专题练习）如图，将一个长方体用过相邻三条棱的中点的平面截出一个棱锥，则该棱锥的体积与剩下的几何体体积的比为 .
26．（2023·上海·高三统考学业考试）如图，在直三棱柱中，是等腰直角三角形.若，则该直三棱柱的体积为 .
27．（2023·青海西宁·统考一模）若甲、乙两个圆柱形容器的容积相等，且甲、乙两个圆柱形的容器内部底面半径的比值为2，则甲、乙两个圆柱形容器内部的高度的比值为 ．
28．（2023秋·江苏镇江·高三江苏省镇江第一中学校考阶段练习）若一个正四棱台的上下底面的边长分别为2和4，侧棱长为，则这个棱台的体积为 ．
29．（2023·全国·高三专题练习）如图，在长方体中，是的中点，则三棱锥的体积为 .
30．（2023·全国·高三专题练习）周总理纪念馆是由正方体和正四棱锥组合体建筑设计，如图所示，若该组合体接于半径R的球O（即所有顶点都在球上），记正四棱锥侧面与正方体底面所成二面角为，则 ．
【B组 在综合中考查能力】
一、单选题
1．（2023·全国·高三专题练习）陀螺又称陀罗，是中国民间最早的娱乐健身玩具之一，在山西夏县新石器时代的遗址中就发现了石制的陀螺.如图所示的陀螺近似看作由一个圆锥与一个圆柱组成的组合体，其中圆柱的底面半径为1，圆锥与圆柱的高均为1，若该陀螺由一个球形材料削去多余部分制成，则球形材料体积的最小值为（ ）
A．B．
C．D．
2．（2023·广东汕头·统考三模）将一个体积为的铁球切割成正三棱锥的机床零件，则该零件体积的最大值为（ ）
A．B．C．D．
3．（2023·浙江绍兴·统考二模）牟合方盖是由我国古代数学家刘徽发现并采用的，一种用于计算球体体积的方法，类似于现在的微元法.由于其采用的模型像一个牟合的方形盒子，故称为牟合方盖.本质上来说，牟合方盖是两个半径相等并且轴心互相垂直的圆柱体相交而成的三维图形，如图1所示.刘徽发现牟合方盖后200多年，祖冲之及他的儿子祖暅，推导出牟合方盖八分之一部分的体积计算公式为（为构成牟合方盖的圆柱底面半径）.图2为某牟合方盖的部分，且图2正方体的棱长为1，则该牟合方盖的体积为（ ）
A．B．C．D．
4．（2023·四川成都·四川省成都列五中学校考三模）一个球体被平面截下的一部分叫做球缺．截面叫做球缺的底面，垂直于截面的直径被截后，剩下的线段长叫做球缺的高，球缺曲面部分的面积，其中R为球的半径，H为球缺的高．如图，若一个半径为R的球体被平面所截获得两个球缺，其高之比为，则表面积（包括底面）之比（ ）
A．B．C．D．
5．（2023·天津河西·天津市新华中学校考模拟预测）灯笼起源于中国的西汉时期，两千多年来，每逢春节人们便会挂起象征美好团圆意义的红灯笼，营造一种喜庆的氛围如图，某球形灯笼的轮廓由三部分组成，上下两部分是两个相同的圆柱的侧面，中间是球面的一部分除去两个球冠如图，球冠是由球面被一个平面截得的，垂直于截面的直径被截得的部分叫做球冠的高，若球冠所在球的半径为，球冠的高为，则球冠的面积已知该灯笼的高为，圆柱的高为，圆柱的底面圆直径为，则围成该灯笼所需布料的面积为（ ）
A．B．
C．D．
6．（2023·重庆·统考模拟预测）如图所示，已知一个球内接圆台，圆台上、下底面的半径分别为和，球的体积为，则该圆台的侧面积为（ ）

A．B．C．D．
7．（2023·辽宁朝阳·朝阳市第一高级中学校考模拟预测）如图，圆台内有一个球，该球与圆台的侧面和底面均相切．已知圆台的下底面圆心为，半径为，圆台的上底面圆心为，半径为（），球的球心为，半径为，记圆台的表面积为，球的表面积为，则的可能的取值为（ ）
A．B．C．D．
8．（2023·天津滨海新·统考三模）某同学参加综合实践活动，设计了一个封闭的包装盒，包装盒如图所示：底面是边长为2的正方形，，，，均为正三角形，且它们所在的平面都与平面垂直，则该包装盒的容积为（ ）

A．B．C．D．20
9．（2023·全国·高三专题练习）如图，已知半径为、母线长为的圆锥的侧面展开图是半圆，在其内部作一个半径为、母线长为的内接圆柱（圆柱的下底面在圆锥的底面上，上底面的圆在圆锥的侧面上），若圆柱的侧面积与圆锥的侧面积之比为，则（ ）

A．B．C．D．
10．（2023秋·山东济南·高三济南市历城第二中学校考开学考试）“方斗”常作为盛米的一种容器，其形状是一个上大下小的正四棱台．在综合实践活动中，某小组在超市中测量出一“方斗”的上底面内侧边长为8dm，下底面内侧边长为2dm，侧棱长为6dm．将“方斗”内的大米铺平（即与下底面平行），测得铺平后的大米所在的四边形边长为6dm．已知1kg大米的体积约为，则方斗内剩余的大米质量约为（参考数据：，，结果保留整数）（ ）
A．30kgB．36kgC．45kgD．52kg
11．（2023·河北·统考模拟预测）在三棱柱中，点D、E分别为棱，的中点，则平面ADE截三棱柱所得两部分的体积比为（ ）
A．2：3B．5：8C．13：23D．19：29
12．（2023·海南·统考模拟预测）古代最初的长度计量常常借助于人体的某一部分或某种动作来实现．《孔子家语》说：“布指知寸，布手知尺，舒肘知寻，斯不远之则也．”“布手知尺”是指中等身材人的大拇指和食指伸开之间的距离，相当于1尺，折合现代的长度约16厘米．古代一位中等身材的农民买到一个正四棱台形状的容器盛粮食，由于没有合适的测量工具，于是用自己的手按上述方式去测量，得到正四棱台的两底面边长分别为3尺和1尺，斜高（侧面梯形的高）为2尺，则按现代的方式计算，该容器的容积约为（ ）（1升＝1000立方厘米，）
A．27升B．31升C．33升D．35升
二、多选题
13．（2023·吉林通化·梅河口市第五中学校考模拟预测）陀螺是中国民间最早的娱乐工具之一，也作陀罗，闽南语称作“干乐”，北方叫作“冰尜（gá）”或“打老牛”．传统古陀螺大致是木制或铁制的倒圆锥形．现有一圆锥形陀螺（如图所示），其底面半径为3，将其放倒在一平面上，使圆锥在此平面内绕圆锥顶点S滚动，当圆锥在平面内转回原位置时，圆锥本身恰好滚动了3周，则（ ）
A．圆锥的母线长为9B．圆锥的表面积为
C．圆锥的侧面展开图（扇形）的圆心角为D．圆锥的体积为
14．（2023·江苏无锡·辅仁高中校考模拟预测）半正多面体亦称“阿基米德多面体”，是由边数不全相同的正多边形围成，体现了数学的对称美.如图，二十四等边体就是一种半正多面体，是由正方体截去八个一样的四面体得到的，若它的所有棱长都为，则（ ）
A．被截正方体的棱长为2
B．被截去的一个四面体的体积为
C．该二十四等边体的体积为
D．该二十四等边体外接球的表面积为
15．（2023·山东淄博·山东省淄博实验中学校考三模）某学校课外社团活动课上，数学兴趣小组进行了一次有趣的数学实验操作，课题名称“不用尺规等工具，探究水面高度”.如图甲，是一个水平放置的装有一定量水的四棱锥密闭容器（容器材料厚度不计），底面为平行四边形，设棱锥高为，体积为，现将容器以棱为轴向左侧倾斜，如图乙，这时水面恰好经过，其中分别为棱的中点，则（ ）
A．水的体积为
B．水的体积为
C．图甲中的水面高度为
D．图甲中的水面高度为
16．（2023·全国·模拟预测）底面为直角三角形的三棱锥的体积为4，该三棱锥的各个顶点都在球O的表面上，点P在底面ABC上的射影为K，，则下列说法正确的是（ ）
A．若点K与点A重合，则球O的表面积的最小值为
B．若点K与点A重合，则球O的体积的最小值为
C．若点K是的斜边的中点，则球O的表面积的最小值为
D．若点K是的斜边的中点，则球O的体积的最小值为
17．（2023·全国·高三专题练习）素描是写实绘画的重要基础，也是最需要理智来协助的艺术．十字贯穿体是学习素描时常用的几何体实物模型，图1所示为一个十字贯穿体的素描作品．十字贯穿体一般是由两个完全相同的正四棱柱“垂直贯穿”构成的多面体，其中一个四棱柱的每一条侧棱分别垂直于另一个四棱柱的每一条侧棱，一个四棱柱的两条相对侧棱和另一个四棱柱的两条相对侧棱各交于两点，另外两条相对侧棱与另一个四棱柱剩下的两条相对侧棱各交于一点（该点为所在棱的中点）．如图2，十字贯穿体由两个底面边长为2、高为6的正四棱柱构成，则（ ）
A．一个正四棱柱的某个侧面与另一个正四棱柱的两个侧面的交线的夹角为钝角
B．该十字贯穿体的表面积是
C．该十字贯穿体的体积是
D．一只蚂蚁从该十字贯穿体的顶点A出发，沿表面到达顶点B的最短路线长为
18．（2023·全国·高三专题练习）如图是一个装有水的全封闭直三棱柱容器若水的体积恰好是该容器体积的一半，容器厚度忽略不计，则（ ）
A．转动容器，当平面水平放置时，容器内水面形成的截面为，则都是所在棱的中点
B．当底面水平放置后，将容器绕着转动（转动过程中始终保持水平），有水的部分是棱柱
C．在翻滚､转动容器的过程中，有水的部分不可能是三棱锥
D．容器中水的体积与直三棱柱外接球体积之比至多为
三、填空题
19．（2023·天津河东·一模）如图所示，一个由圆锥和圆柱组成的玻璃容器，中间联通（玻璃壁厚度忽略不计），容器中装有一定体积的水，圆柱高为10，底面半径为3，圆锥高为，底面半径大于圆柱，左图中，圆柱体在下面，液面保持水平，高度为，右图中将容器倒置，水恰好充满圆锥，则圆锥底面的半径为 ．
20．（2023春·河北石家庄·高三石家庄二中校考阶段练习）根据祖暅原理，界于两个平行平面之间的两个几何体，被任一平行于这两个平面的平面所截，如果两个截面的面积相等，则这两个几何体的体积相等．如图1所示，一个容器是半径为R的半球，另一个容器是底面半径和高均为R的圆柱内嵌一个底面半径和高均为R的圆锥，这两个容器的容积相等．若将这两容器置于同一平面，注入等体积的水，则其水面高度也相同．如图2，一个圆柱形容器的底面半径为，高为，里面注入高为的水，将一个半径为的实心球缓慢放入容器内，当球沉到容器底端时，水面的高度为 ．（注：）
21．（2023·广东·高三专题练习）已知直四棱柱的棱长均为2，，除面ABCD外，该四棱柱其余各个面的中心分别为点E，F，G，H，Ⅰ，则由点E，F，G，H，Ⅰ构成的四棱锥的体积为 ．
22．（2023·全国·模拟预测）如图，在四棱锥中，，，过AB的平面分别交PD，PC于点E，F，且，记四棱锥的体积为，几何体ABCDEF的体积为，则 .
23．（2023·黑龙江齐齐哈尔·统考二模）表面积为36π的球M表面上有A，B两点，且为等边三角形，空间中的动点P满足，当点P在所在的平面内运动时，点P的轨迹是 ；当P在该球的球面上运动时，点P的轨迹长度为 .
24．（2023·江西南昌·校联考模拟预测）在一次手工劳动课上，需要把一个高为3，体积为的木质实心圆锥模型削成一个实心球模型，则球的表面积的最大值为 .
25．（2023·全国·高三专题练习）如图，一个棱长为6分米的正方体形封闭容器中盛有V升的水，若将该容器任意放置均不能使水平面呈三角形，则V的取值范围是 ．
26．（2023·贵州·统考模拟预测）如图，某环保组织设计一款苗木培植箱，其外形由棱长为2（单位：）的正方体截去四个相同的三棱锥（截面为等腰三角形）后得到.若将该培植箱置于一球形环境中，则该球表面积的最小值为
27．（2023春·贵州·高三校联考阶段练习）如图，若正方体的棱长为2，点是正方体的上底面上的一个动点（含边界），，分别是棱，上的中点，有以下结论：
①在平面上的投影图形的面积为定值；
②平面截该正方体所得的截面图形是五边形；
③的最小值是；
④若保持，则点在上底面内运动路径的长度为
其中正确的是 .（填写所有正确结论的序号）
【C组 在创新中考查思维】
一、单选题
1．（2023·湖南益阳·安化县第二中学校考三模）如图所示，该几何体是由两个全等的直四棱柱相嵌而成的，且前后、左右、上下均对称，两个四棱柱的侧棱互相垂直，已知该几何体外接球的体积为，四棱柱的底面是正方形，且侧棱长为4，则两个直四棱柱公共部分的几何体的内切球体积为（ ）

A．B．C．D．
2．（2023·重庆沙坪坝·重庆一中校考模拟预测）“牟合方盖”是由我国古代数学家刘徽首先发现并采用的一种用于计算球体体积的方法，当一个正方体用圆柱从纵横两侧面作内切圆柱体时，两圆柱体的公共部分即为“牟合方盖”，他提出“牟合方盖”的内切球的体积与“牟合方盖”的体积比为定值，南北朝时期祖暅提出理论：“缘幂势既同，则积不容异”，即“在等高处的截面面积总是相等的几何体，它们的体积也相等”，并算出了“车合方盖”和球的体积，其大体思想可用如图表示，其中图1为棱长为的正方体截得的“牟合方盖”的八分之一，图2为棱长为的正方体的八分之一，图3是以底面边长为r的正方体的一个底面和底面以外的一个顶点作的正四棱锥，则根据祖暅原理，下列结论正确的为（ ）

A．若以一个平行于正方体上下底面的平面，截“牟合方盖”，截面是一个圆形．
B．图2中阴影部分的面积为．
C．由棱长为的正方体截得的“牟合方盖”体积为．
D．“牟合方盖”的内切球的体积与“牟合方盖”的体积比为．
3．（2023·黑龙江哈尔滨·哈九中校考模拟预测）已知平面上两定点、，则所有满足（且）的点的轨迹是一个圆心在上，半径为的圆.这个轨迹最先由古希腊数学家阿波罗尼斯发现，故称作阿氏圆.已知棱长为3的正方体表面上动点满足，则点的轨迹长度为（ ）
A．B．C．D．
4．（2023·浙江·校联考模拟预测）中国古代数学著作《九章算术》记载了一种被称为“曲池”的几何体，该几何体的上、下底面平行，且均为扇环形（扇环是指圆环被扇形截得的部分）．现有一个如图所示的曲池，它的高为2，，、，均与曲池的底面垂直，底面扇环对应的两个圆的半径分别为1和2，对应的圆心角为，则图中四面体的体积为（ ）．
A．B．1C．D．
5．（2023·全国·高三专题练习）在直三棱柱中，，且分别为和的中点，为线段（包括端点）上一动点，为侧面上一动点，则的最小值为（ ）
A．B．
C．D．
6．（2023·全国·高三专题练习）在棱长为1的正方体中，动点P在棱上，动点Q在线段上、若，则三棱锥的体积（ ）
A．与无关，与有关B．与有关，与无关
C．与都有关D．与都无关
7．（2023·全国·高三专题练习）我们把底面是正三角形，顶点在底面的射影是正三角形中心的三棱锥称为正三棱锥.现有一正三棱锥放置在平而上，已知它的底面边长为2，高，该正三棱锥绕边在平面上转动（翻转），某个时刻它在平面上的射影是等腰直角三角形，则的取值范围是（ ）
A．B．C．D．
二、多选题
8．（2023·江苏扬州·江苏省高邮中学校考模拟预测）如图，已知正四棱柱的底面边长为1，侧棱长为2，点分别在半圆弧（均不含端点）上，且在球上，则（ ）

A．当点在的三等分点处，球的表面积为
B．球的表面积的取值范围为
C．当点在的中点处，过三点的平面截正四棱柱所得的截面的形状都是四边形
D．当点在的中点处，三棱锥的体积为定值
9．（2023春·广东深圳·高三校考阶段练习）如图，圆锥的轴截面是边长为2的正三角形，圆锥的内接圆柱的底面半径为，圆柱的体积为，则（ ）
A．圆锥的表面积为
B．圆柱的体积最大值为
C．圆锥的外接球体积为
D．
三、填空题
10．（2023·广东东莞·统考模拟预测）以棱长为的正四面体中心点为球心，半径为的球面与正四面体的表面相交部分总长度为 .
11．（2023·全国·高三专题练习）正方体容器中盛满水，，分别是的中点，若个小孔分别位于三点处，则正方体中的水最多会剩下原体积的 .（用分数表示）
12．（2023·山东日照·三模）祖暅，南北朝时代的伟大科学家，他在实践的基础上提出了祖暅原理：“幂势既同，则积不容异”，即夹在两个平行平面之间的两个几何体，被平行于这两个平面的任意平面所截，如果截得的两个截面的面积总相等，那么这两个几何体的体积相等.请同学们借助图1运用祖暅原理解决如下问题：如图2，有一个倒圆锥形容器，它的轴截面是一个正三角形，在容器内放一个半径为2的铁球，再注入水，使水面与球正好相切（球与倒圆锥相切效果很好，水不能流到倒圆锥容器底部），则容器中水的体积为 .

13．（2023·辽宁锦州·校考一模）在正四棱锥中，为的中点，过作截面将该四棱锥分成上､下两部分，记上､下两部分的体积分别为，则的最大值是 .等级
24h降雨量（精确到0.1）
……
……
小雨
0.1~9.9
中雨
10.0~24.9
大雨
25.0~49.9
暴雨
50.0~99.9
……
……