高中数学人教A版 (2019)必修 第一册3.4 函数的应用（一）多媒体教学课件ppt

这是一份高中数学人教A版 (2019)必修 第一册3.4 函数的应用（一）多媒体教学课件ppt，共25页。PPT课件主要包含了常见函数模型，文字语言，符号语言，函数模型的应用，实际问题，数学模型，数学模型的解，抽象概括，推理演算，方法总结等内容，欢迎下载使用。

到目前为止，我们已经学习了哪些常用函数？
一次函数: y=ax+b (a≠0)二次函数: y=ax2 +bx+c (a≠0)幂 函 数: y=xα
函数应用要做好“翻译”工作：
图形(图表)语言
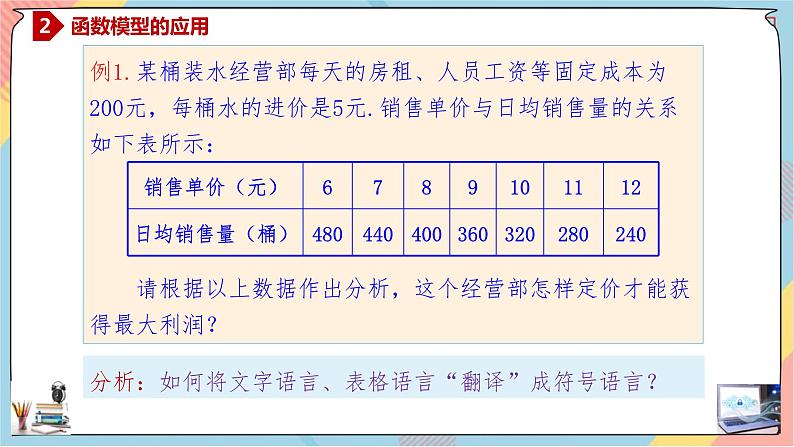
例1.某桶装水经营部每天的房租、人员工资等固定成本为200元，每桶水的进价是5元.销售单价与日均销售量的关系如下表所示： 请根据以上数据作出分析，这个经营部怎样定价才能获得最大利润？
分析：如何将文字语言、表格语言“翻译”成符号语言？
解：根据表可知，销售单价每增加1元，日均销售量就减少40桶. 设在进价基础上增加x元后，日均销售利润为y元，而在此情况下的日均销售量为： 480-40（x-1)=520-40x（桶） 由于x>0, 且520-40x>0,即0于是可得 y=(520-40x)x-200 =-40x2+520x-200, 0步骤总结：先将表格语言“翻译”成符号语言：日均销售量为520-40x；再根据问题实际意义确定自变量的范围；然后给出利润表达式； 最后根据函数模型确定最值.
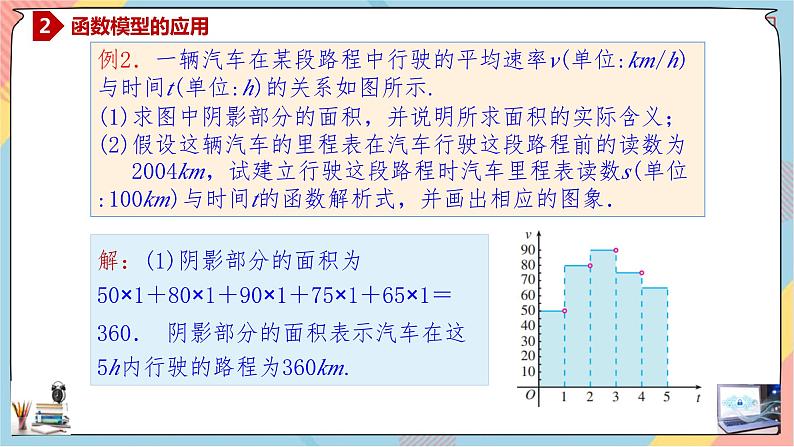
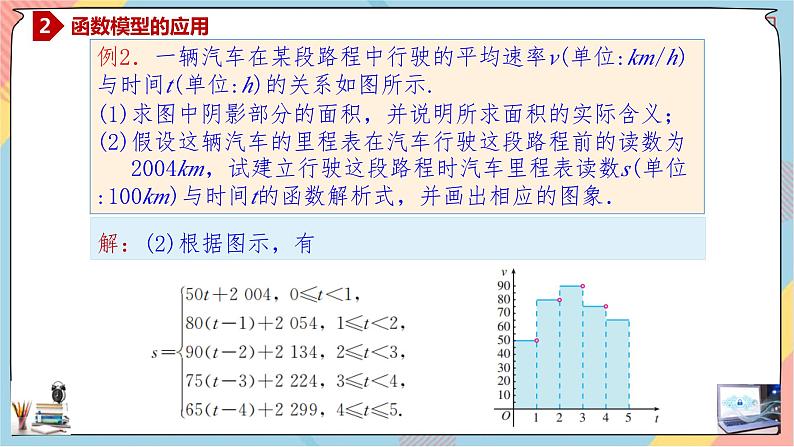
例2．一辆汽车在某段路程中行驶的平均速率v(单位:km/h)与时间t(单位:h)的关系如图所示. (1)求图中阴影部分的面积，并说明所求面积的实际含义； (2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为 2004km，试建立行驶这段路程时汽车里程表读数s(单位:100km)与时间t的函数解析式，并画出相应的图象．
解：(1)阴影部分的面积为50×1＋80×1＋90×1＋75×1＋65×1＝360． 阴影部分的面积表示汽车在这5h内行驶的路程为360km.
解：(2)根据图示，有
解：(2)这个函数的图象如图所示.
实际问题 的解
使用数学模型解决实际问题的基本步骤如下：
例3．某车间有30名木工，要制作200把椅子和100张课桌，已知制作一张课桌与制作一把椅子的工时之比为10：7，问30名工人应当如何分组(一组制作课桌，另一组制作椅子)，才能保证最快完成全部任务？
分析：完成全部任务的时间就是两组中需要用时较多的那组所用的时间，因此要想最快完成任务，两组所用时间之差应为0或越小越好.
则完成全部任务所需时间 t(x)= max{ f(x),g(x) }
答：用13名工人制作课桌，17名工人制作椅子，最快完成 全部任务.
1.某公司市场营销部的个人月收入与其每月的销售量成一次函数关系，其图象如图所示，由图中给出的信息可知，营销人员没有销售量时的收入是_____.
2.某工厂8年来某产品的总产量y与时间t(年)的函数关系如图所示，则①前3年总产量增长速度越来越快；②前3年总产量增长速度越来越慢；③第3年后，这种产品停止生产；④第3年后，这种产品年产量持续增长．上述说法中正确的是_________.
【分析】 由图可知前3年的总产量增长速度是越来越快； 而图象在t∈(3,8)上平行于t轴，说明总产量没有变化，所以第3年后该产品停止生产.因此只有①③正确.【答案】①③
3.某商场把商品A按标价的八折售出，仍可获利30%， 若商品A的进价为100元，则标价是 .
【解析】 设标价为x，则实际售价为80%x，获利30%， 所以(80%x－100)÷100＝30%⇒x＝162.5.
4.以墙为一边，用篱笆围成长方形的场地，再用平行于一边的篱笆隔开，已知篱笆的总长为定值 l，则这块场地的最大面积为 .
一、本节课学习的新知识
二、本节课提升的核心素养
三、本节课训练的数学思想方法
基础作业： .
能力作业： .