初中数学苏科版九年级上册1.2 一元二次方程的解法教学ppt课件

这是一份初中数学苏科版九年级上册1.2 一元二次方程的解法教学ppt课件，共42页。PPT课件主要包含了教学目标，知识精讲，问题引入，x2+12x-27，x+629，配方法，xx+224，x2+2x24，x+1225，配方法的应用等内容，欢迎下载使用。

掌握用配方法解二次项系数为1的一元二次方程的一般步骤
掌握用配方法解二次项系数不为1的一元二次方程的一般步骤
能够应用配方法解决比较大小、求最值、求参求值等问题
配方法——二次项系数为1
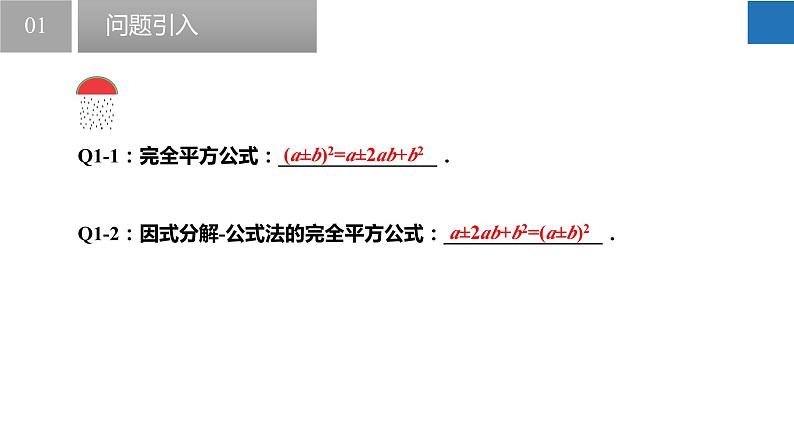
Q1-1：完全平方公式：________________．
(a±b)2=a±2ab+b2
Q1-2：因式分解-公式法的完全平方公式：________________．
a±2ab+b2=(a±b)2
Q1-3：先填空，再观察并说明等号左边常数项与一次项系数之间的关系（1）x2+2x+____=(x+1)2；（2）x2-4x+____=(x-2)2；（3）x2+6x+____=(x+____)2；（4）x2-2px+____=(x-____)2（5）x2+hx+____=(x+____)2．
【结论】常数项=一次项系数一半的平方
Q2-1：x2+12x+27=0的解为________________．
若增加一个条件：“已知(x+6)2-9=0的解为x1=-3，x2=-9”呢？
无法直接开平方，怎么办？
Q2-2：已知(x+6)2-9=0的解为x1=-3，x2=-9，则x2+12x+27=0的解为________________．
【分析】∵(x+6)2=9等价于x2+12x+27=0∴x2+12x+27=0即(x+6)2-9=0的解
x1=-3，x2=-9
用完全平方公式展开(x+6)2=9：x2+12x+36=9x2+12x+27=0
x2+2·x·6+62=-27+62
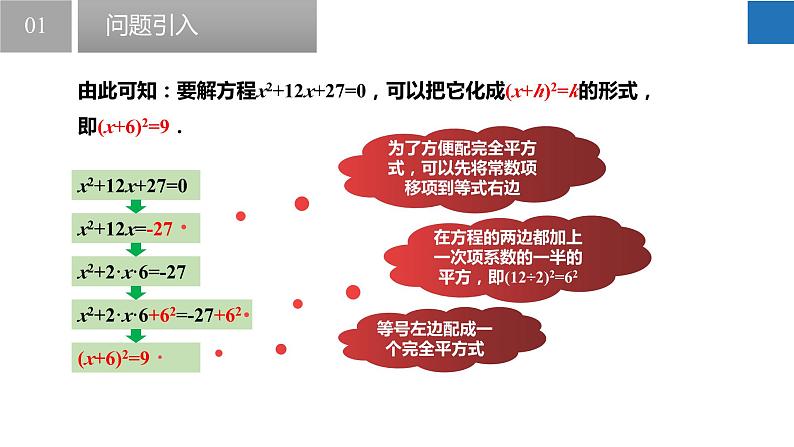
由此可知：要解方程x2+12x+27=0，可以把它化成(x+h)2=k的形式，即(x+6)2=9．
x2+12x+27=0
为了方便配完全平方式，可以先将常数项移项到等式右边
x2+2·x·6=-27
在方程的两边都加上一次项系数的一半的平方，即(12÷2)2=62
等号左边配成一个完全平方式
1.定义：把一个一元二次方程变形为(x+h)2=k的形式，当k≥0时，就可以用直接开平方法求出方程的解，这种解一元二次方程的方法叫做配方法．
【探究1】解方程：x2-18x+1=0．
【探究2】解方程：x2-7x+6=0．
【探究3】解方程：x2+14x+49=0．
【解答】①配方：(x+7)2=0②直接开平方：x+7=±0即x1=x2=-7
【探究4】解方程：x2+5x+7=0．
【探究5】用配方法解一元二次方程x2+2x-24=0，配方的过程可以用拼图直观地表示．
【分析】把方程x2+2x-24=0变形为x2+2x=24，即x(x+2)=24．配方的过程，可以看成将一个长是(x+2)、宽是x、面积是24的矩形割补成一个正方形．
一个矩形通过割、拼、补，成为一个正方形的过程
x2+2x+12=24+12
配方法——二次项系数不为1
【探究6】解方程：2x2-x-3=0．
【分析】把二次项系数化为1，即方程两边同时除以二次项系数．
当一元二次方程的二次项系数不为1时，怎么办？
【探究8】解方程：2x2-x+1=0．
【配方法-二次项系数为1】
例1、解方程：x(x-6)-7=0．
【解答】x2-6x-7=0x2-6x=7x2-2·x·3+32=7+32(x-3)2=16x-3=±4即x1=7，x2=-1
例2-1、解方程：2x2+4x-5=0．
【配方法-二次项系数不为1】
例2-2、解方程：4x2+12x+9=0．
例2-3、解方程：3x2-8x+7=0．
例3、已知m=2b+2022，n=b2+2025，则m和n的大小关系中正确的是（　　）A．m＞nB．m≥nC．m＜nD．m≤n
【分析】∵m=2b+2022，n=b2+2025，∴n-m=b2-2b+3=b2-2b+1+2=(b-1)2+2>0，∴n>m．
【解题方法与策略】作差法①作差②配完全平方式，使得差变形为“a( )2+b( )2+c”的形式③根据完全平方式的非负性判断差的正负
练3-1、已知M=2x2-2x+3，N=4x2-3x+4，请比较M和N的大小．
对二次项、一次项提二次项系数，再配方
练3-2、若A=x2+2x+2y，B=-y2+4x-3，则A、B的大小关系为（　　）A．A＞BB．A＜BC．A=BD．无法确定
【分析】∵A-B=x2+2x+2y+y2-4x+3=x2+2x+1+(y2+2y+1)+1=(x+1)2+(y+1)2+1＞0，∴A＞B．
不含xy项，x2、y2分开配方
练3-3、已知任意实数满足等式x=a2-4ab+4b2，y=4a-8b-5，则x、y的大小关系是（　　）A．x=yB．x＞yC．x＜yD．x≥y
【分析】∵x-y=a2-4ab+4b2-4a+8b+5=(a-2b)2-4(a-2b)+4+1=[(a-2b)-2]2+1＞0，∴x＞y．
a2-4ab+4b2必须放在一起配完全平方式，若a2、4b2分开去配，则多余的-4ab无法判断正负
将(a-2b)看作一个整体，第二次配方
例4、求代数式x2-10x+5的最小值．
【分析】x2-10x+5=x2-10x+25-20=(x-5)2-20，当(x-5)2=0，即x=5时，代数式取最小值为-20．
【解题策略】①配完全平方式，使得代数式变形为“a( )2+b( )2+c”的形式②根据完全平方式的非负性，当a( )2=b( )2=0时，代数式取最值c
练4-1、求代数式-2x2+10x+1的最大值．
练4-2、求多项式x2-6x+4y2+4y+20的最小值．
【解答】原式=x2-6x+9+(4y2+4y+1)+10=(x-3)2+(2y+1)2+10，∵(x-3)2≥0，(2y+1)2≥0，∴原式≥10（当x-3=0，2y+1=0时取等号），∴最小值是10．
【求值求参——“0+0=0”】
例5、已知a2+b2-4a-6b+13=0，求(a-b)2023的值．
【分析】∵a2+b2-4a-6b+13=0，∴a2-4a+4+(b2-6b+9)=0，∴(a-2)2+(b-3)2=0，∴a=2，b=3，∴(a-b)2023=(2-3)2023=-1．
【解题策略】①配完全平方式，使得等式变形为“a( )2+b( )2=0”的形式②根据完全平方式的非负性可得：a( )2=b( )2=0
练5-1、若a、b为有理数，且2a2-2ab+b2-6a+9=0，求a+2b的值．
【分析】∵2a2-2ab+b2-6a+9=0，∴a2-2ab+b2+(a2-6a+9)=0，∴(a-b)2+(a-3)2=0，∴a-b=0，a-3=0，∴a=b=3，∴a+2b=9．
-2ab+b2配成完全平方式只需要一个a2
练5-2、已知a、b、c满足a2+b2+c2-6a+2b-4c+14=0，求(ab)c的值．
【分析】∵a2+b2+c2-6a+2b-4c+14=0，∴a2-6a+9+(b2+2b+1)+(c2-4c+4)=0，∴(a-3)2+(b+1)2+(c-2)2=0，解得：a=3，b=-1，c=2，∴(ab)c=(-3)2=9．