初中1.2 一元二次方程的解法图片ppt课件

这是一份初中1.2 一元二次方程的解法图片ppt课件，共28页。PPT课件主要包含了教学目标，公式法，知识精讲，问题引入，根的判别式等内容，欢迎下载使用。

熟记求根公式，掌握用公式法解一元二次方程的一般步骤
能够根据根的判别式判断一元二次方程的根的情况
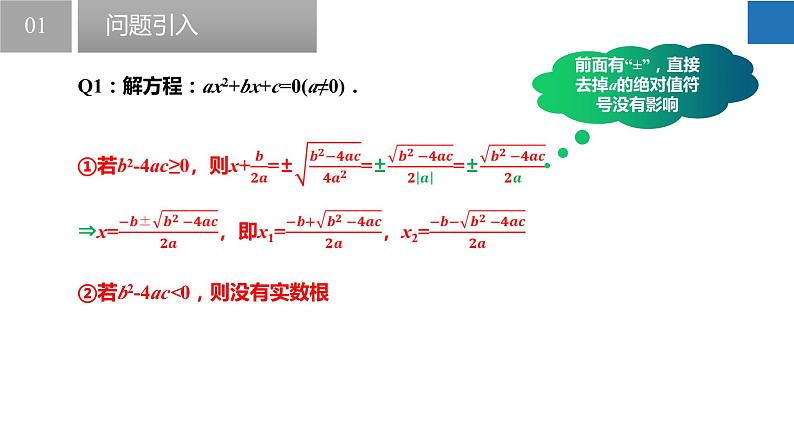
Q1：解方程：ax2+bx+c=0(a≠0)．
∵a≠0，∴4a2>0，
②若b2-4ac<0，则没有实数根
前面有“±”，直接去掉a的绝对值符号没有影响
Q2：通过Q1的解方程，你发现了什么？
1.2公式法的定义：解一元二次方程时，把各项系数的值直接代入求根公式，若b²-4ac≥0，就可以求得方程的根，这种解一元二次方程的方法叫做公式法．
【探究1】解方程：x2+3x+1=0．
【探究2】解方程：3x2=4x-1．
注意：不是一般形式，不可以直接确定a、b、c的值哦~
1.3用公式法解一元二次方程的一般步骤：①把方程化成一般形式（建议二次项系数为正，且方程中无分数），②确定a、b、c的值（注意符号）；③求出b2-4ac的值（若b2-4ac＜0，则无实数根）；④在b2-4ac≥0的前提下，把a、b、c的值代入公式进行计算求出方程的根．
注意：用公式法解一元二次方程的前提条件有两个：①a≠0；②b²-4ac≥0．
建议：二次项系数不为正，可先化为正 ：方程两边同时乘以-1
【解答】①方程两边同时乘以2：x2+6x+10=0，②确定a、b、c的值：a=1，b=6，c=10，③求出b2-4ac的值：b2-4ac=62-4×1×10=-4<0，即方程无实数根．
建议：方程中含有分数，可先去分母 ：方程两边同时乘以2
【探究5】通过下列表格，对一元二次方程ax2+bx+c=0(a≠0)的根的情况进行总结．
2.2一元二次方程ax2+bx+c=0(a≠0)的根的情况如下：①当Δ>0时，有两个不相等的实数根；②当Δ=0时，有两个相等的实数根；③当Δ<0时，没有实数根．
2.1根的判别式：我们把Δ=b2-4ac叫做一元二次方程ax2+bx+c=0(a≠0)的根的判别式．
【探究6】判断下列一元二次方程的根的情况：（1）x2+2x-5=0；（2）2x2-5x+6=0；（3）x2+1=2x；（4）x2+kx+k-1=0．
【解答】（1）∵a=1，b=2，c=-5，∴Δ=b2-4ac=22-4×1×(-5)=24>0，∴方程有两个不相等的是实数根；
【分析】求出Δ的值，判断正负即可
（2）∵a=2，b=-5，c=6，∴Δ=b2-4ac=(-5)2-4×2×6=-23<0，∴方程没有实数根；
（3）x2-2x+1=0，∵a=1，b=-2，c=1，∴Δ=b2-4ac=(-2)2-4×1×1=0，∴方程有两个相等的是实数根；
（4）∵a=1，b=k，c=k-1，∴Δ=b2-4ac=k2-4×1×(k-1)=(k-2)2≥0，∴方程有两个实数根．
例1-1、解方程：3x2-6x-2=0．
例1-2、解方程：(k2-4)x2-(5k-2)x+6=0．
【分析】x2前面的系数含参，则该系数可能为0，也可能不为0，若该系数为0，则方程不是一元二次方程，若该系数不为0，则方程是一元二次方程，故本题需分类讨论．
前面有“±”，直接去掉k-10的绝对值符号没有影响
【利用求根公式反求一元二次方程】
【根据根的判别式判断一元二次方程的根的情况】
例3-1、已知关于x的方程，x2-(k+1)x+k=0，则下列说法正确的是（　　）A．不存在k的值，使得方程有两个相等的实数解B．至少存在一个k的值，使得方程没有实数解C．无论k为何值，方程总有两个实数根D．无论k为何值，方程有两个不相等的实数根
【分析】∵a=1，b=-(k+1)，c=k，∴Δ=b2-4ac=[-(k+1)]2-4k=(k-1)2≥0，∴此方程有两个实数根．
练3-2、定义新运算：a◎b=ab-b2，例如1◎2=1×2-22=2-4=-2，则方程2◎x=5的根的情况是（　　）A．有两个不相等的实数根B．有两个相等的实数根C．没有实数根 D．只有一个实数根
【分析】根据新运算2◎x=2x-x2=5，即x2-2x+5=0，∵a=1，b=-2，c=5，∴Δ=b2-4ac=(-2)2-4×1×5=-16＜0，∴方程没有实数根．
【利用一元二次方程的根的情况反求参】
例4-1、如果关于x的一元二次方程k2x2-(2k+1)x+1=0有两个不相等的实数根，求k的取值范围．
例4-2、若关于x的方程(m-2)x2-3x-1=0有实数根，求m的取值范围．