初中数学苏科版九年级上册1.4 用一元二次方程解决问题背景图课件ppt

这是一份初中数学苏科版九年级上册1.4 用一元二次方程解决问题背景图课件ppt，共29页。PPT课件主要包含了教学目标，知识精讲，问题引入，图形面积问题，增长率问题，降低率问题，商品销售问题，动态几何问题，数字问题等内容，欢迎下载使用。

能够由实际问题抽象出一元二次方程，掌握用一元二次方程解决问题的一般步骤
能够用一元二次方程解决图形面积问题、增长率问题、商品销售问题、动态几何问题、数字问题等
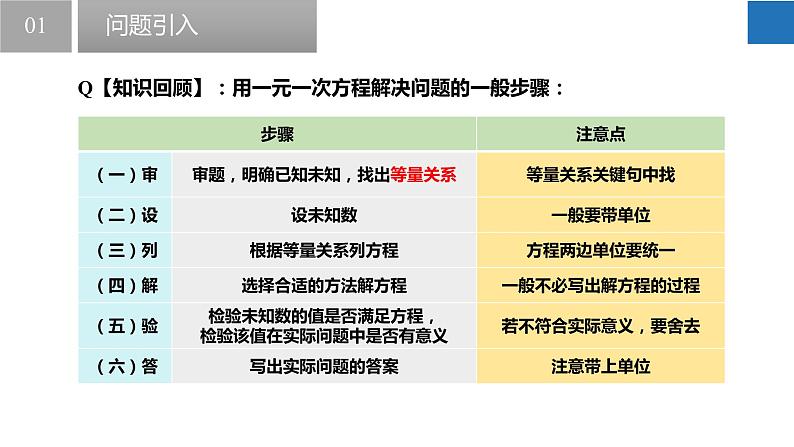
Q【知识回顾】：用一元一次方程解决问题的一般步骤：
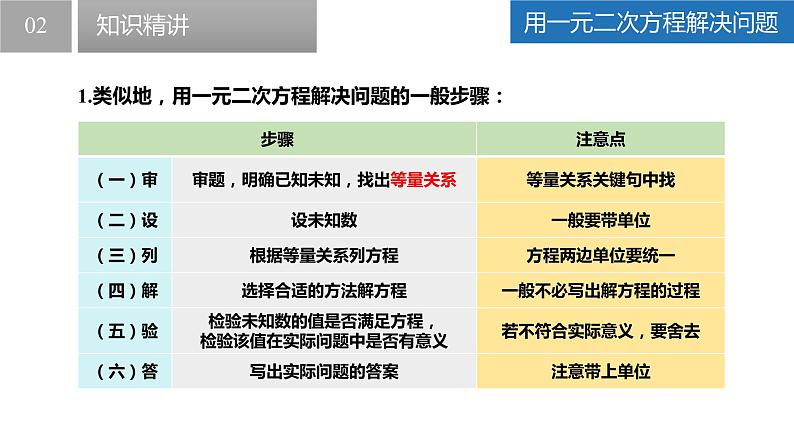
1.类似地，用一元二次方程解决问题的一般步骤：
用一元二次方程解决问题
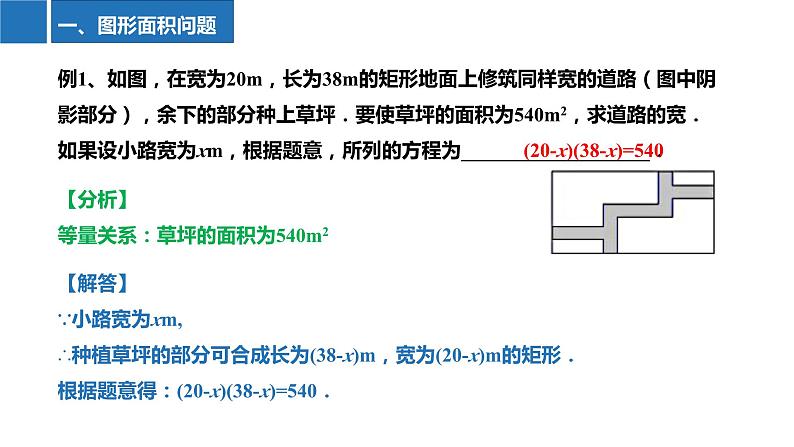
例1、如图，在宽为20m，长为38m的矩形地面上修筑同样宽的道路（图中阴影部分），余下的部分种上草坪．要使草坪的面积为540m2，求道路的宽．如果设小路宽为xm，根据题意，所列的方程为___________________．
【解答】∵小路宽为xm,∴种植草坪的部分可合成长为(38-x)m，宽为(20-x)m的矩形．根据题意得：(20-x)(38-x)=540．
(20-x)(38-x)=540
【分析】等量关系：草坪的面积为540m2
练1、如图，用一面足够长的墙为一边，其余三边用总长36米的围栏建两个面积相同的生态园，由于场地限制，垂直于墙的一边长不超过6米．（围栏宽忽略不计）（1）每个生态园的面积为48平方米，求每个生态园的边长；（2）每个生态园的面积能否达到60平方米？请说明理由．
【分析】（1）等量关系：生态园的面积为48平方米
练1、如图，用一面足够长的墙为一边，其余三边用总长36米的围栏建两个面积相同的生态园，由于场地限制，垂直于墙的一边长不超过6米．（围栏宽忽略不计）（2）每个生态园的面积能否达到60平方米？请说明理由．
【分析】（2）等量关系：生态园的面积为60平方米
eg：若原数是a，每次增长的百分率为x，则第一次增长后为a(1+x)；第二次增长后为a(1+x)2．
例2、小区新增了一家快递店，第一天揽件200件，第三天揽件242件，设该快递店揽件日平均增长率为x，则根据题意可列方程为___________________．
200(1+x)2=242
【分析】等量关系：200(1+x)2=242
练2、某网络学习平台2021年的新注册用户数为100万，2023年的新注册用户数为169万，设新注册用户数的年平均增长率为x(x＞0)，则x=_______．
【解答】根据题意得：100(1+x)2=169，解得：x1=0.3=30%，x2=-2.3（不合题意，舍去），∴x的值为30%．
【分析】等量关系：100(1+x)2=169
eg：若原数是a，每次降低的百分率为x，则第一次降低后为a(1-x)；第二次降低后为a(1-x)2．
例3、某一芯片实现国产化后，经过两次降价，每块芯片单价由256元降为196元．若两次降价的百分率相同，设每次降价的百分率为x，则根据题意可列方程为___________________．
256(1-x)2=196
【分析】等量关系：256(1-x)2=196
练3、某商品原价每件75元，两次降价后每件48元，则平均每次的降价百分率是_______．
【解答】设平均每次的降价百分率是x,根据题意得：75(1-x)2=48，解得：x1=0.2=20%，x2=1.8（不合题意，舍去），∴平均每次的降价百分率是20%．
【分析】等量关系：75(1-x)2=48
设平均每次的降价百分率是x
例4、某商店经销一批小家电，每个小家电成本40元，经市场预测，定价为50元时，可销售200个，定价每增加1元，销售量将减少10个，如果商店进货后全部销售完，赚了2160元，该小家电定价是____________元．
【分析】等量关系：每个的销售利润×销售数量=总利润2160元
【解答】设该小家电定价时x元，则每个的销售利润为(x-40)元，可销售[200-10(x-50)]个，根据题意得：(x-40)[200-10(x-50)]=2160，整理得：x2-110x+3016=0，解得：x1=52，x2=58，经检验，两解成立，∴该小家电定价是52元或58元．
练4、某商店销售甲、乙两种商品，甲的成本为5元，乙的成本为7元．甲现在的售价为10元，每天卖出30个；售价每提高1元，每天少卖出2个．乙现在的售价为14元，每天卖出6个；售价每降低1元，每天多卖出4个．假定甲、乙两种商品每天卖出的数量和不变（和为36袋），且售价均为整数．（1）当甲的售价提高x元，乙的售价为__________元；（用含x的代数式表示）（2）当甲的售价提高多少元时，销售这两种商品当天的总利润是268元？
【分析】（2）等量关系：甲的销售利润×甲的销售数量+乙的销售利润×乙的销售数量=总利润268元
例5、如图，在Rt▲ABC中，∠C=90°，AC=12cm，BC=9cm．现有动点P从点A出发，沿AC向点C方向运动，动点Q从点C出发，沿线段CB向点B方向运动，如果点P的速度是2cm/s，点Q的速度是1cm/s，它们同时出发，当有一点到达所在线段的端点时，就停止运动．设运动的时间为ts，当t为何值时，Rt▲CPQ的面积等于5cm2？
如图③，当3＜t≤4时，根据题意得：PC=8-2t，CQ=t，∴(8-2t)2+t2=5，整理得：5t2-32t+59=0，∵Δ=322-4×5×59=-156＜0，∴该方程没有实数根；
例6、一个两位数，个位上的数字比十位上的数字小4，且个位数字与十位数字的平方和比这两位数小4，设个位数字为x，则可列方程为_____________________．
【解答】根据题意得：十位数字是(x+4)，这个两位数是[10(x+4)+x]，∴x2+(x+4)2=10(x+4)+x-4．
【分析】等量关系：(个位数字)2+(十位数字)2=这个两位数-4
x2+(x+4)2=10(x+4)+x-4
练6、一个两位数，个位数字比十位数字大3，个位数字的平方刚好等于这个两位数，则这个两位数是多少？
【解答】设个位数字为x，则十位数字是(x-3)，这个两位数是[10(x-3)+x]，根据题意得：x2=10(x-3)+x，整理得：x2-11x+30=0，解得：x1=5，x2=6，当x=5时，x-3=2，则这个两位数是25；当x=6时，x-3=3，则这个两位数是36；答：这个两位数是25或36．
【分析】等量关系：(个位数字)2=这个两位数