第10讲 用空间向量研究直线、平面的位置关系4种常见方法归类-新高二数学暑假衔接试题（人教版）

这是一份第10讲 用空间向量研究直线、平面的位置关系4种常见方法归类-新高二数学暑假衔接试题（人教版），文件包含第10讲用空间向量研究直线平面的位置关系4种常见方法归类教师版-新高二暑假衔接人教版docx、第10讲用空间向量研究直线平面的位置关系4种常见方法归类学生版-新高二暑假衔接人教版docx等2份试卷配套教学资源，其中试卷共91页， 欢迎下载使用。
1.理解与掌握直线的方向向量，平面的法向量.
2.会用方向向量，法向量证明线线、线面、面面间的平行关系；会用平面法向量证明线面和面面垂直，并能用空间向量这一工具解决与平行、垂直有关的立体几问题.
知识点1 空间中点、直线和平面的向量表示
1．空间直线的向量表示式
设A是直线上一点，a是直线l的方向向量，在直线l上取eq \(AB,\s\up6(→))＝a，设P是直线l上任意一点，
(1)点P在直线l上的充要条件是存在实数t，使eq \(AP,\s\up6(→))＝ta，即eq \(AP,\s\up6(→))＝teq \(AB,\s\up6(→)).
(2)取定空间中的任意一点O，点P在直线l上的充要条件是存在实数t.使eq \(OP,\s\up6(→))＝eq \(OA,\s\up6(→))＋ta.
(3)取定空间中的任意一点O，点P在直线l上的充要条件是存在实数t，使eq \(OP,\s\up6(→))＝eq \(OA,\s\up6(→))＋teq \(AB,\s\up6(→)).
注意点：
(1)空间中，一个向量成为直线l的方向向量，必须具备以下两个条件：①是非零向量；②向量所在的直线与l平行或重合．
(2)直线上任意两个不同的点都可构成直线的方向向量．与直线l平行的任意非零向量a都是直线的方向向量，且直线l的方向向量有无数个．
(3)空间任意直线都可以由直线上一点及直线的方向向量唯一确定．
2．空间平面的向量表示式
①如图，设两条直线相交于点O，它们的方向向量分别为a和b，P为平面α内任意一点，由平面向量基本定理可知，存在唯一的有序实数对(x，y)，使得eq \(OP,\s\up6(→))＝xa＋yb.
②如图，取定空间任意一点O，空间一点P位于平面ABC内的充要条件是存在实数x，y，使eq \(OP,\s\up6(→))＝eq \(OA,\s\up6(→))＋xeq \(AB,\s\up6(→))＋yeq \(AC,\s\up6(→)).我们把这个式子称为空间平面ABC的向量表示式．
③由此可知，空间中任意平面由空间一点及两个不共线向量唯一确定．
如图，直线l⊥α，取直线l的方向向量a，我们称向量a为平面α的法向量．给定一个点A和一个向量a，那么过点A，且以向量a为法向量的平面完全确定，可以表示为集合{P|a·eq \(AP,\s\up6(→))＝0}．
注意点：
(1)平面α的一个法向量垂直于平面α内的所有向量．
(2)一个平面的法向量有无限多个，它们相互平行．
易错辨析：
（1）空间中给定一个点A和一个方向向量能唯一确定一条直线吗？答案：能
（2）一个定点和两个定方向向量能否确定一个平面？答案：不一定，若两个定方向向量共线时不能确定，若两个定方向向量不共线能确定．
（3）由空间点A和直线l的方向向量能表示直线上的任意一点？答案：能
知识点2 空间平行、垂直关系的向量表示
1、理解直线方向向量的概念
(1)直线上任意两个不同的点都可构成直线的方向向量．
(2)直线的方向向量不唯一．
2、利用待定系数法求法向量的步骤
3、求平面法向量的三个注意点
（1）选向量：在选取平面内的向量时，要选取不共线的两个向量
（2）取特值：在求n的坐标时，可令x，y，z中一个为一特殊值得另两个值，就是平面的一个法向量
（3）注意0：提前假定法向量n＝(x，y，z)的某个坐标为某特定值时一定要注意这个坐标不为0
4、用空间向量证明平行的方法
(1)线线平行：证明两直线的方向向量共线．
(2)线面平行：
①证明直线的方向向量与平面内任意两个不共线的向量共面，即可用平面内的一组基底表示．
②证明直线的方向向量与平面内某一向量共线，转化为线线平行，利用线面平行判定定理得证．
③先求直线的方向向量，然后求平面的法向量，证明直线的方向向量与平面的法向量垂直．
在证明线面平行时，需注意说明直线不在平面内．
(3)面面平行：①证明两平面的法向量为共线向量；②转化为线面平行、线线平行问题．
5、用空间向量证明垂直的方法
(1)线线垂直：证明两直线的方向向量互相垂直，即证明它们的数量积为零．
(2)线面垂直：①基向量法：选取基向量，用基向量表示直线所在的向量，证明直线所在向量与两个不共线向量的数量积均为零，从而证得结论．
②坐标法：建立空间直角坐标系，求出直线方向向量的坐标，证明直线的方向向量与两个不共线向量的数量积均为零，从而证得结论．
③法向量法：建立空间直角坐标系，求出直线方向向量的坐标以及平面法向量的坐标，然后说明直线方向向量与平面法向量共线，从而证得结论．
(3)面面垂直：证明两个平面的法向量垂直，或将面面垂直的判定定理用向量表示．
考点一：求直线的方向向量
例1．（2023春·高二课时练习）如图，在四棱锥P－ABCD中，底面ABCD为矩形，PA⊥平面ABCD，E为PD的中点，AB＝AP＝1，AD＝，试建立恰当的空间直角坐标系，求直线PC的一个方向向量．
变式1．（2023春·高二课时练习）已知直线的一个方向向量为，另一个方向向量为，则________， ________.
变式2．（2022秋·广西钦州·高二校考阶段练习）已知直线的一个法向量是，则的倾斜角的大小是（ ）
A．B．C．D．
变式3．【多选】（2022秋·湖北十堰·高二校联考阶段练习）如图，在正方体中，E为棱上不与，C重合的任意一点，则能作为直线的方向向量的是（ ）
A．B．C．D．
变式4．（2023春·江苏常州·高二校联考期中）已知直线l的一个方向向量，且直线l过A(0，y，3)和B(－1，2，z)两点，则y－z等于（ ）
A．0B．1C．2D．3
考点二：求平面的法向量
例2．（2023春·四川成都·高二四川省成都市新都一中校联考期中）已知，，，则平面ABC的一个法向量可以是（ ）
A．B．C．D．
变式1．（2023春·高二课时练习）已知，则平面的一个单位法向量是（ ）
A．B．
C．D．
变式2．（2023春·福建龙岩·高二校联考期中）《九章算术》中，将四个面都为直角三角形的四面体称为鳖臑.在鳖臑中，平面，，.若建立如图所示的“空间直角坐标系，则平面的一个法向量为（ ）

A．B．C．D．
变式3．（2023秋·高二课时练习）在如图所示的坐标系中，为正方体，给出下列结论：
①直线的一个方向向量为；
②直线的一个方向向量为；
③平面的一个法向量为；
④平面的一个法向量为.其中正确的个数为（ ）

A．1个B．2个C．3个D．4个
变式4．（2023·全国·高三专题练习）放置于空间直角坐标系中的棱长为2的正四面体ABCD中，H是底面中心，平面ABC，写出：平面BHD的一个法向量___________；
变式5．（2023春·高二课时练习）在棱长为2的正方体中，E，F分别为棱的中点，在如图所示的空间直角坐标系中，求：
(1)平面的一个法向量；
(2)平面的一个法向量.
变式6．【多选】（2023春·福建宁德·高二校联考期中）已知空间中三个向量，，，则下列说法正确的是（ ）
A．与是共线向量B．与同向的单位向量是
C．在方向上的投影向量是D．平面ABC的一个法向量是
变式7．（2023春·四川成都·高二成都市锦江区嘉祥外国语高级中学校考期中）已知，分别是平面，的法向量，则平面，交线的方向向量可以是（ ）
A．B．C．D．
变式8．（2023秋·福建南平·高二统考期末）已知四面体ABCD的顶点坐标分别为，，，．
(1)若M是BD的中点，求直线CM与平面ACD所成的角的正弦值；
(2)若P，A，C，D四点共面，且BP⊥平面ACD，求点P的坐标．
变式9．（2023春·湖北·高二校联考阶段练习）已知点在平面内，是平面的一个法向量，则下列点中，在平面内的是（ ）
A．B．C．D．
变式10．（2023春·河南·高二临颍县第一高级中学校联考开学考试）已知点在平面内，平面，其中是平面的一个法向量，则下列各点在平面内的是（ ）
A．B．C．D．
考点三：用空间向量证明平行问题判断直线、平面的位置关系
例3．（2023秋·湖北黄石·高二校考阶段练习）若直线l的一个方向向量为，平面α的一个法向量为，则（ ）
A．l∥α或l⊂αB．l⊥α
C．l⊂αD．l与α斜交
变式1．（2023春·高二单元测试）若平面与的法向量分别是，，则平面与的位置关系是（ ）
A．平行B．垂直C．相交不垂直D．无法判断
变式2．（2023春·山东菏泽·高二统考期末）已知平面与平面是不重合的两个平面，若平面α的法向量为，且，，则平面与平面的位置关系是________.
变式3．（2023秋·陕西宝鸡·高二统考期末）在长方体中，，以点为坐标原点，以分别为轴，轴，轴建立空间直角坐标系，设对角面所在法向量为，则__________．
变式4．【多选】（2023春·甘肃张掖·高二高台县第一中学校考期中）下列利用方向向量、法向量判断线、面位置关系的结论中正确的是（ ）
A．若两条不重合直线，的方向向量分别是，，则
B．若直线的方向向量，平面的法向量是，则
C．若两个不同平面，的法向量分别为，，则
D．若平面经过三点，，，向量是平面的法向量，则
（二）已知直线、平面的平行关系求参数
例4．（2022秋·广东广州·高二广州市第九十七中学校考阶段练习）直线的方向向量是，平面的法向量，若直线平面，则______．
变式1．（2023秋·上海浦东新·高二上海南汇中学校考期末）已知直线的一个方向向量为，平面的一个法向量，若，则实数_______．
变式2．（2022秋·天津蓟州·高二校考期中）直线的方向向量是，平面的法向量，若直线，则___________.
变式3．（2023春·上海·高二校联考阶段练习）已知平面的一个法向量为，平面的一个法向量为，若，则的值为______
（三）证明直线、平面的平行问题
例5．（2022春·江苏镇江·高二江苏省镇江第一中学校联考期末）如图，三棱柱中侧棱与底面垂直，且AB＝AC＝2，AA1＝4，AB⊥AC，M，N，P，D分别为CC1，BC，AB，的中点．
求证：PN∥面ACC1A1；
变式1．（2023·天津和平·耀华中学校考二模）如图，四棱锥中，侧面PAD为等边三角形，线段AD的中点为O且底面ABCD，，，E是PD的中点．

证明：平面PAB；
变式2．（2023·湖北黄冈·浠水县第一中学校考模拟预测）如图，在三棱柱中，平面，D，E分别为棱AB，的中点，，，.
证明：平面；
变式3．（2023春·江苏盐城·高二盐城市大丰区南阳中学校考阶段练习）如图，在三棱锥中，底面，．点，，分别为棱，，的中点，是线段的中点，，．
求证：平面；
变式4．（2023·天津南开·南开中学校考模拟预测）在四棱锥中，底面，且，四边形是直角梯形，且，，，，为中点，在线段上，且.

求证：平面；
变式5．（2023·四川成都·校考一模）如图，在四棱锥中，底面为矩形，平面平面，，，，，分别是，的中点.

求证：平面；
变式6．（2021·高二课时练习）如图，在长方体中，点E，F，G分别在棱，，上，；点P，Q，R分别在棱，CD，CB上，．求证：平面平面PQR．
变式7．（2023·上海普陀·曹杨二中校考模拟预测）如图所示，正四棱柱ABCD﹣A1B1C1D1的底面边长1，侧棱长4，AA1中点为E，CC1中点为F．
求证：平面BDE∥平面B1D1F；
考点四：利用空间向量证明垂直问题
（一）判断直线、平面的位置关系
例6．（2021秋·北京·高二校考期中）直线的方向向量分别为，则（ ）
A．B．∥C．与相交不平行D．与重合
变式1．（2022秋·北京·高二校考阶段练习）若直线l的方向向量为，平面的法向量为，则直线l和平面位置关系是（ ）
A．B．C．D．不确定
变式2．【多选】（2022秋·广东珠海·高二珠海市斗门区第一中学校考期末）已知为直线l的方向向量,分别为平面,的法向量（,不重合）,那么下列说法中正确的有（ ）．
A．B．
C．D．
变式3．（2023春·江苏·高二南师大二附中校联考阶段练习）下列利用方向向量､法向量判断线､面位置关系的结论中，正确的是（ ）
A．两条不重合直线的方向向量分别是，则
B．直线的方向向量，平面的法向量是，则
C．两个不同的平面的法向量分别是，则
D．直线的方向向量，平面的法向量是，则
变式4．【多选】（2022·高二课时练习）下列命题是真命题的有( )
A．A，B，M，N是空间四点，若不能构成空间的一个基底，那么A，B，M，N共面
B．直线l的方向向量为，直线m的方向向量为，则l与m垂直
C．直线l的方向向量为，平面α的法向量为，则l⊥α
D．平面α经过三点，是平面α的法向量，则u+t＝1
（二）已知直线、平面的垂直关系求参数
例7．（2023春·北京海淀·高二中央民族大学附属中学校考开学考试）已知平面的法向量为，直线的方向向量为，则下列选项中使得的是（ ）
A．B．
C．D．
变式1．（江苏省扬州市2022-2023学年高二下学期6月期末数学试题）已知直线的方向向量为，平面的法向量为.若，则的值为（ ）
A．B．C．1D．4
变式2．（2023春·高二课时练习）已知是直线l的方向向量，是平面的法向量．若，则______．
变式3．（2022秋·广东珠海·高二珠海市实验中学校考阶段练习）若直线l方向向量为，平面的法向量为，且，则m为（ ）
A．1B．2C．4D．
变式4．（2023春·江苏盐城·高二江苏省响水中学校考阶段练习）如图，在正三棱锥D-ABC中，，，O为底面ABC的中心，点P在线段DO上，且，若平面PBC，则实数（ ）
A．B．C．D．
（三）证明直线、平面的垂直问题
例8．（2023春·高二课时练习）如图，在三棱锥P－ABC中，AB＝AC，D为BC的中点，PO⊥平面ABC，垂足O落在线段AD上．已知BC＝8，PO＝4，AO＝3，OD＝2.
(1)证明：AP⊥BC；
(2)若点M是线段AP上一点，且AM＝3，试证明AM⊥平面BMC.
变式1．（2023秋·高二课时练习）如图，在棱长为1的正方体中，分别是的中点，建立适当的空间直角坐标系，证明：．

变式2．（2023春·江苏连云港·高二统考期中）如图，在多面体中，，，都是边长为2的等边三角形，平面平面，平面平面．

(1)判断，，，四点是否共面，并说明理由；
(2)在中，试在边的中线上确定一点，使得平面．
变式3．（2023·安徽合肥·合肥市第八中学校考模拟预测）如图，在三棱柱中，底面是等腰三角形，且，又侧棱，面对角线，点分别是棱的中点，.

证明：平面；
变式4．（2023·河北唐山·唐山市第十中学校考模拟预测）如图，在四棱台中，平面平面ABCD，底面ABCD为正方形，，.

求证：平面.
变式5．（2023春·高二课时练习）如图所示，△ABC是一个正三角形，EC⊥平面ABC，BD∥CE，且CE＝CA＝2BD.求证：平面DEA⊥平面ECA.
变式6．（2022秋·全国·高二专题练习）如图，在四棱锥中，平面，底面是梯形，点E在上，．
求证：平面平面；
变式7．（2022秋·广东深圳·高二深圳外国语学校校考期末）已知：在四棱锥中，底面为正方形，侧棱平面，点为中点，．
求证：平面平面；
1．如图，在正四棱柱中，．点分别在棱,上，．

证明：；
2．如图，在长方体中，E、P分别是的中点，分别是的中点，．
求证：面；
3．如图所示，四棱锥的底面是边长为1的菱形，是的中点，底面，．
证明：平面平面；
4．如图，直三棱柱中，，，，侧棱，侧面的两条对角线交点为D，的中点为M．
求证：平面；
5．如图，在棱长为1的正方体中，点是棱的中点，点是棱上的动点．
(1)试确定点的位置，使得平面；
6．如图，正三棱柱的所有棱长都为2，D为中点．
求证：平面；
7．如图1，已知是上．下底边长分别为2和6，高为的等腰梯形，将它沿对称轴折成直二面角，如图2．
证明：；
8．如图，在棱长为1的正方体中，与交于点E，与交于点F．
求证：平面；
一、单选题
1．（2023春·高二课时练习）若在直线l上，则直线l的一个方向向量为（ ）
A．B．
C．D．
2．（2023秋·天津河北·高二天津外国语大学附属外国语学校校考期末）如图，在三棱锥中，底面，，，，D为棱的中点，则异面直线与所成角的余弦值为（ ）
A．B．C．D．
3．（2023秋·广西柳州·高二校考期末）已知直线，则下列结论正确的个数是（ ）
①直线的截距为
②向量是直线的一个法向量
③过点与直线平行的直线方程为
④若直线，则
A．B．C．D．
4．（2023·江苏·高二专题练习）不重合的两条直线，的方向向量分别为，．不重合的两个平面，的法向量分别为，，直线，均在平面，外．下列说法中错误的是（ ）
A．B．
C．D．
5．（2023·全国·高二专题练习）如图，在空间直角坐标系中，有正方体，给出下列结论：
①直线的一个方向向量为；
②直线的一个方向向量为；
③平面的一个法向量为；
④平面的一个法向量为．
其中正确的个数为（ ）．
A．1B．2C．3D．4
6．（2023·江苏·高二专题练习）若，分别为直线，的一个方向向量，则（ ）．
A．B．与相交，但不垂直
C．D．不能确定
7．（2023·全国·高三专题练习）设向量是直线l的方向向量，是平面α的法向量，则（ ）
A．B．或C．D．
8．（2023春·高二课时练习）已知平面内的两个向量= (2，3，1)，= (5，6，4)，则该平面的一个法向量为（ ）
A．(1，－1，1)B．(2，－1，1)
C．(－2，1，1)D．(－1，1，－1)
9．（2023春·高二课时练习）设，是不重合的两个平面，，的法向量分别为，，和是不重合的两条直线，，的方向向量分别为，，那么的一个充分条件是（ ）
A．，，且，B．，，且
C．，，且D．，，且
10．（2023春·河南商丘·高二商丘市第一高级中学校考阶段练习）直线的方向向量为，平面的法向量为，若，则（ ）
A．-2B．2C．6D．10
11．（2023春·安徽·高二合肥市第八中学校联考开学考试）已知点在平面内，是平面的一个法向量，则下列点P中，在平面内的是（ ）
A．B．C．D．
二、填空题
12．（2023春·四川成都·高二四川省成都市新都一中校联考期中）已知直线l在平面外，直线l的方向向量是，平面的法向量是，则l与的位置关系是___________（填“平行”或“相交”）
13．（2023春·高二课时练习）设平面的一个法向量分别为，则的位置关系为________．
14．（2023春·高二课时练习）若平面的一个法向量为，平面的一个法向量为，且，则 ________.
15．（2023春·高二课时练习）已知是直线l的一个方向向量，是平面α的一个法向量，若l⊥α，则a，b的值分别为________.
二、多选题
16．（2023春·广西南宁·高二校联考开学考试）若是平面的一个法向量，是平面的一个法向量，，是直线上不同的两点，则以下命题正确的是（ ）
A．
B．
C．，使得
D．设与的夹角为，则
17．（2023春·福建莆田·高二莆田华侨中学校考期中）以下命题正确的是（ ）．
A．直线l的方向向量，直线m的方向向量，则
B．直线l的方向向量，平面的法向量，则或
C．两个不同平面，的法向量分别为，，则
D．平面经过三点，，，向量是平面的法向量，则，
18．（2023秋·江西宜春·高二校考期末）已知空间中三点，，，则下列结论正确的有（ ）
A．
B．与共线的单位向量是
C．与夹角的余弦值是
D．平面的一个法向量是
19．（2023秋·江西宜春·高二统考期末）已知空间中三点，则下列结论正确的有（ ）
A．B．与共线的单位向量是
C．与夹角的余弦值是D．平面的一个法向量是
20．（2023秋·河北沧州·高二统考期末）在正四面体ABCD中，E，F是BC，AD的中点，平面ADE的法向量为，则下列结论正确的是（ ）
A．B．
C．是平面BCF的法向量D．
21．（2023春·江苏南京·高二校考阶段练习）下列结论正确的是（ ）
A．直线的方向向量，平面的法向量，则
B．两个不同的平面，的法向量分别是，，则
C．若直线的方向向量，平面的法向量，若，则实数
D．若，，，则点在平面内
四、解答题
22．（2023·北京·北京四中校考模拟预测）如图，正三棱柱中，分别是棱上的点，.

证明：平面平面；
23．（2023春·福建宁德·高二校联考期中）在正四棱柱中，，，E在线段上，且.

求证：平面DBE；
24．（2023春·江苏淮安·高二金湖中学校联考阶段练习）如图所示，在直四棱柱中，，，，，.
证明：；
25．（2023秋·云南大理·高二统考期末）如图，在四棱锥中，平面，，四边形满足，，，点M为PC的中点.

求证：；
26．（2023春·江苏扬州·高二统考期中）如图，在三棱柱中，底面是边长为2的等边三角形，分别是线段的中点，在平面内的射影为.

(1)求证：平面；
27．（2023春·福建龙岩·高二校联考期中）如图，在四棱锥中，底面ABCD，底面ABCD是矩形，，，E是PA的中点，，.

证明：平面DEF.
28．（2023·山东菏泽·山东省鄄城县第一中学校考三模）已知在直三棱柱中，其中为的中点，点是上靠近的四等分点，与底面所成角的余弦值为．

求证：平面平面；
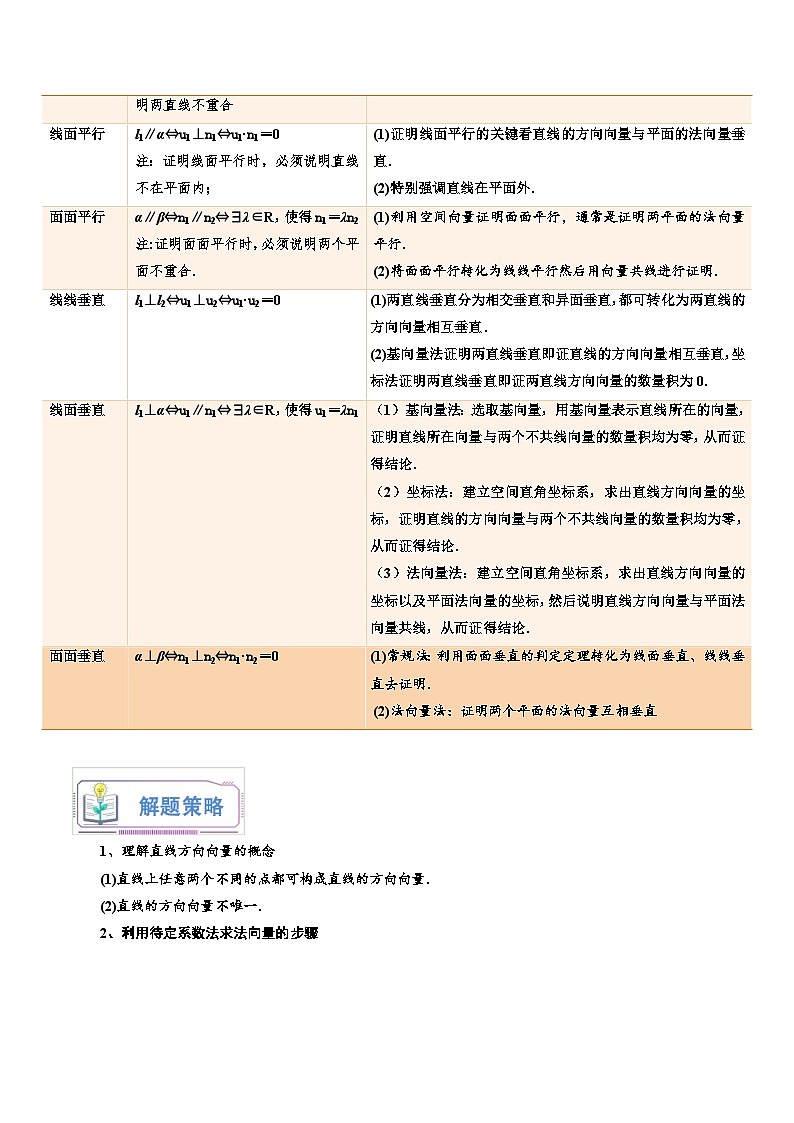
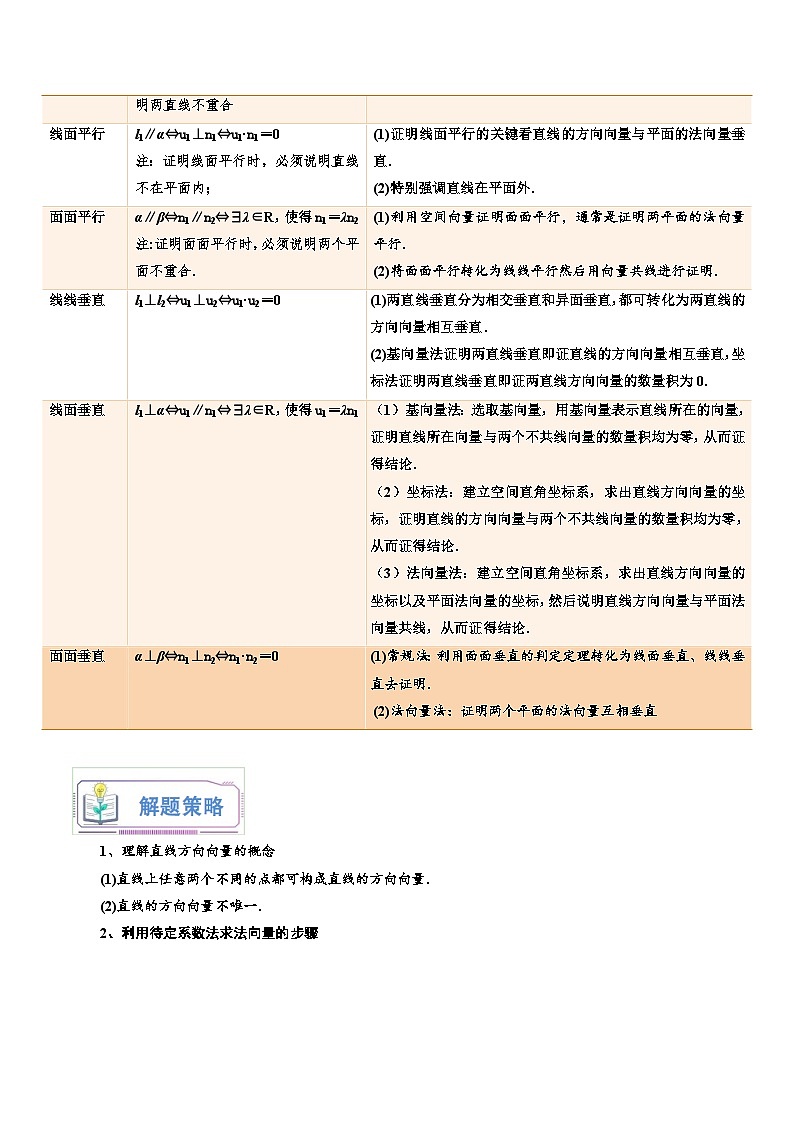
设u1，u2分别是直线l1，l2的方向向量，n1，n2分别是平面α，β的法向量．
线线平行
l1∥l2⇔u1∥u2⇔∃λ∈R，使得u1＝λu2
注：此处不考虑线线重合的情况．但用向量方法证明线线平行时，必须说明两直线不重合
证明线线平行的两种思路：①用基向量表示出要证明的两条直线的方向向量，通过向量的线性运算，利用向量共线的充要条件证明．②建立空间直角坐标系，通过坐标运算，利用向量平行的坐标表示．
线面平行
l1∥α⇔u1⊥n1⇔u1·n1＝0
注：证明线面平行时，必须说明直线不在平面内；
(1)证明线面平行的关键看直线的方向向量与平面的法向量垂直．
(2)特别强调直线在平面外．
面面平行
α∥β⇔n1∥n2⇔∃λ∈R，使得n1＝λn2
注:证明面面平行时，必须说明两个平面不重合．
(1)利用空间向量证明面面平行，通常是证明两平面的法向量平行．
(2)将面面平行转化为线线平行然后用向量共线进行证明．
线线垂直
l1⊥l2⇔u1⊥u2⇔u1·u2＝0
(1)两直线垂直分为相交垂直和异面垂直，都可转化为两直线的方向向量相互垂直．
(2)基向量法证明两直线垂直即证直线的方向向量相互垂直，坐标法证明两直线垂直即证两直线方向向量的数量积为0.
线面垂直
l1⊥α⇔u1∥n1⇔∃λ∈R，使得u1＝λn1
（1）基向量法：选取基向量，用基向量表示直线所在的向量，证明直线所在向量与两个不共线向量的数量积均为零，从而证得结论．
（2）坐标法：建立空间直角坐标系，求出直线方向向量的坐标，证明直线的方向向量与两个不共线向量的数量积均为零，从而证得结论．
（3）法向量法：建立空间直角坐标系，求出直线方向向量的坐标以及平面法向量的坐标，然后说明直线方向向量与平面法向量共线，从而证得结论．
面面垂直
α⊥β⇔n1⊥n2⇔n1·n2＝0
(1)常规法：利用面面垂直的判定定理转化为线面垂直、线线垂直去证明．
(2)法向量法：证明两个平面的法向量互相垂直