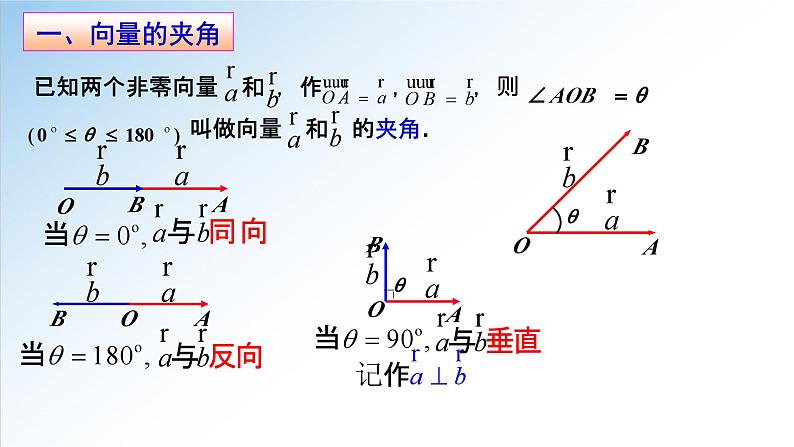
高中数学人教A版 (2019)必修 第二册6.2 平面向量的运算课文内容ppt课件

这是一份高中数学人教A版 (2019)必修 第二册6.2 平面向量的运算课文内容ppt课件，共22页。PPT课件主要包含了知识回顾，数乘定义，向量的夹角，例1已知，向量的投影，投影向量，θ90º，θ0º，θ180º，︱cosθ︱≤1等内容，欢迎下载使用。
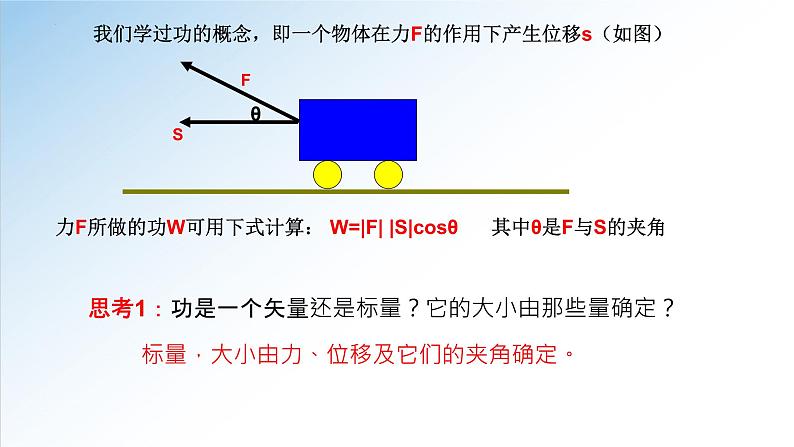
我们学过功的概念，即一个物体在力F的作用下产生位移s（如图）
力F所做的功W可用下式计算： W=|F| |S|csθ 其中θ是F与S的夹角
思考1：功是一个矢量还是标量？它的大小由那些量确定？
标量，大小由力、位移及它们的夹角确定。
思考2：如果我们将公式中的力与位移类比推广到两个一般向量，其 结果又该如何表述？
两个向量的大小及其夹角余弦的乘积。
　　功是力与位移的大小及其夹角余弦的乘积；
二、平面向量的数量积的定义
（1）两向量的数量积是一个数量，而不是向量，符号由夹角决定.
（2） a · b中间的“ · ”在向量的运算中不能省略，也不能写 成a×b ，a×b 表示向量的另一种运算（外积）．
（3） 在运用数量积公式解题时，一定要注意两向量夹角的范围是 [ 0°，180°]．
思考3：向量的数量积是一个数量，那么它什么时候为正，什么时候为负？
数量积符号由cs的符号所决定
解：由 得
因为 所以 。
四、平面向量的数量积的性质
设 是非零向量，它们的夹角是 ，是与 方向相同的单位向量，则
五、平面向量的数量积的运算律
思考4：向量的数量积满足结合律 吗？
例3.对任意 ，恒有 ， 对任意向量 ，是否也有下面类似的结论？
例5.已知 为单位向量，且 的夹角 为 ，求向量 在 上的投影向量。
解：向量 在 上的投影向量为
[例7] 已知|a|=6,|b|=4,(a+2b)·(a-3b)=-72,则a与b的夹角为　　　　. 
例8.已知 且 与 不共线，当k取何值时，向量 与 互相垂直？
解： 与 互相垂直的充要条件是
所以，当 时， 与 互相垂直。