人教A版 (2019)选择性必修 第三册6.2 排列与组合图片ppt课件

这是一份人教A版 (2019)选择性必修 第三册6.2 排列与组合图片ppt课件，共19页。PPT课件主要包含了组合的定义，排列的定义，排列数公式，探究新知，直观解释，课本P25，巩固训练，用组合数回答等内容，欢迎下载使用。
一般地，从n个不同元素中取出m(m≤n)个元素作为一组，叫做从n个不同元素中取出m个元素的一个组合(cmbinatin).
一般地，从n个不同元素中取出m(m≤n)个元素，按照一定的顺序排成一列，叫做从 n 个不 同元素中取出 m 个元素的一个排列.
类比排列数，我们引进组合数概念：
回顾：从甲、乙、丙3名同学中选出2名参加一项活动，有多少种不同的选法？
取出2个元素的组合的个数是排列数的一半
因此组合数
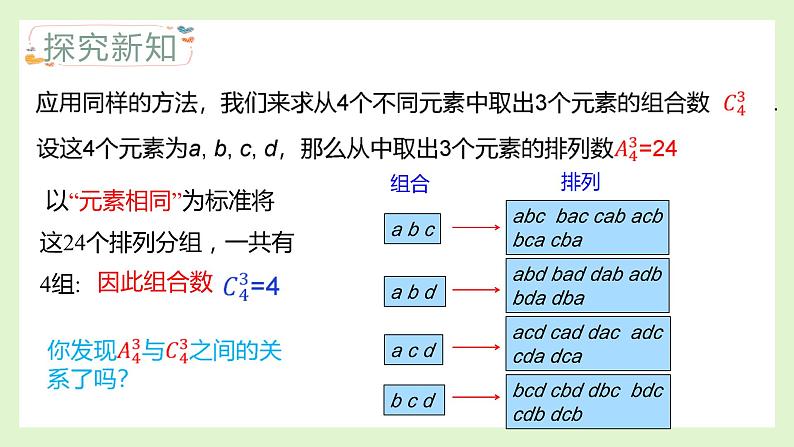
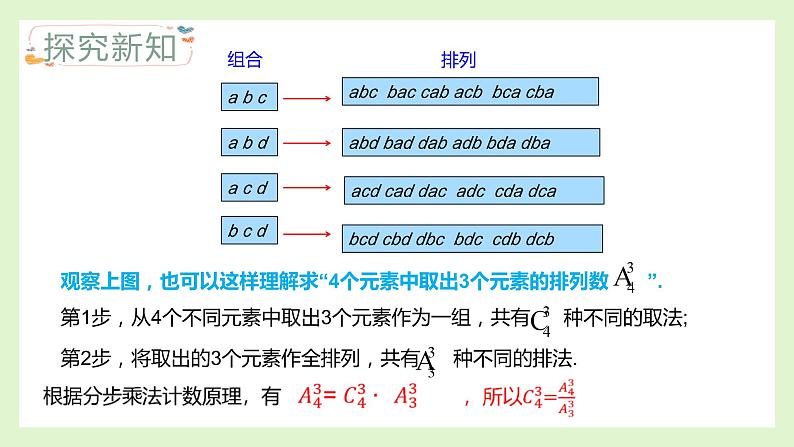
以“元素相同”为标准将 这24个排列分组，一共有4组:
这里n,m∈N* ，并且m≤n. 这个公式叫做组合数公式.
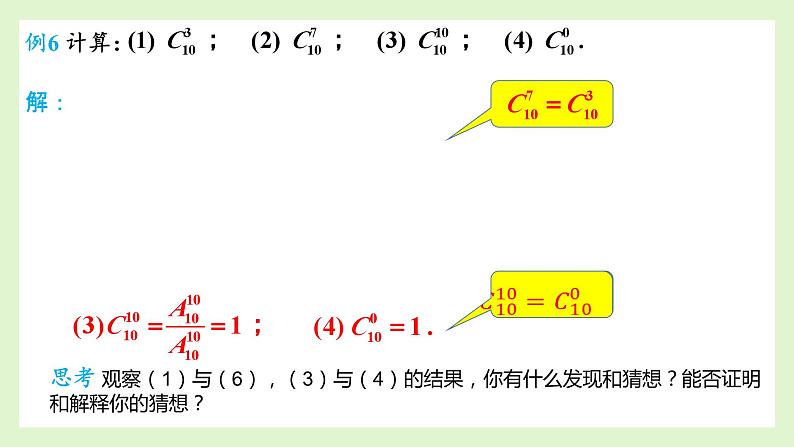
思考 观察（1）与（6），（3）与（4）的结果，你有什么发现和猜想？能否证明和解释你的猜想？
该性质反映了组合数的对称性. 其组合意义是从n个不同的元素中任取m个元素的组合与从n个不同的元素中任取(n-m)个元素的组合是一一对应(一种取法对应一种剩法).
追问：观察练习1的计算结果，你有什么发现和猜想？能否证明和解释你的猜想？
直观解释： “从(n+1)个不同元素中取m个元素作为一组”可以分为两类：
例7 在100件产品中, 有98件合格品, 2件次品. 从这100件产品中任意抽出3件. (1) 有多少种不同的抽法? (2) 抽出的3件中恰好有1件是次品的抽法有多少种? (3) 抽出的3件中至少有1件是次品的抽法有多少种?
(1) 所有的不同抽法种数，就是从100件产品中抽出3件的组合数，所以抽法种数为
从100件产品抽出的3件中至少有1件是次品，包括有1件次品和有2件次品两种情况，因此根据分类加法计数原理，抽出的3件中至少有1件是次品的抽法种数为
抽出的3 件中至少有1件是次品的抽法种数，就是从100件产品中抽出3件的抽法种数减去3件都是合格品的抽法种数，即
3. 有政治、历史、地理、物理、化学、生物这6门学科的学业水平考试成绩，现要从中选3门考试成绩. (1) 共有多少种不同的选法? (2) 如果物理和化学恰有1门被选，那么共有多少种不同的选法? (3) 如果物理和化学至少有1门被选，那么共有多少种不同的选法?