










初中数学人教版九年级上册21.2.2 公式法一等奖教学课件ppt
展开1. 会用公式法解一元二次方程。2. 理解用根的判别式判别根的情况。3. 通过推导求根公式的过程,极强推理能力的训练,进一步发展逻辑思维能力,体验类比、转化、降次的数学思想。
【提问】简述通过配方法解一元二次方程的步骤。
【注意】配方的关键:利用已知两项a2±2ab来确定第三项,只要二次项系数为1,则第三项一定是b2 .
【问题】用配方法解一元二次方程: ax2+bx+c=0(a≠0)?
因为a≠0,所以4a2>0,式子b2-4ac的值需分情况讨论:
1)若b2-4ac>0
方程有两个不相等的实数根
2)若b2-4ac=0
方程有两个相等的实数根
3)若b2-4ac<0,
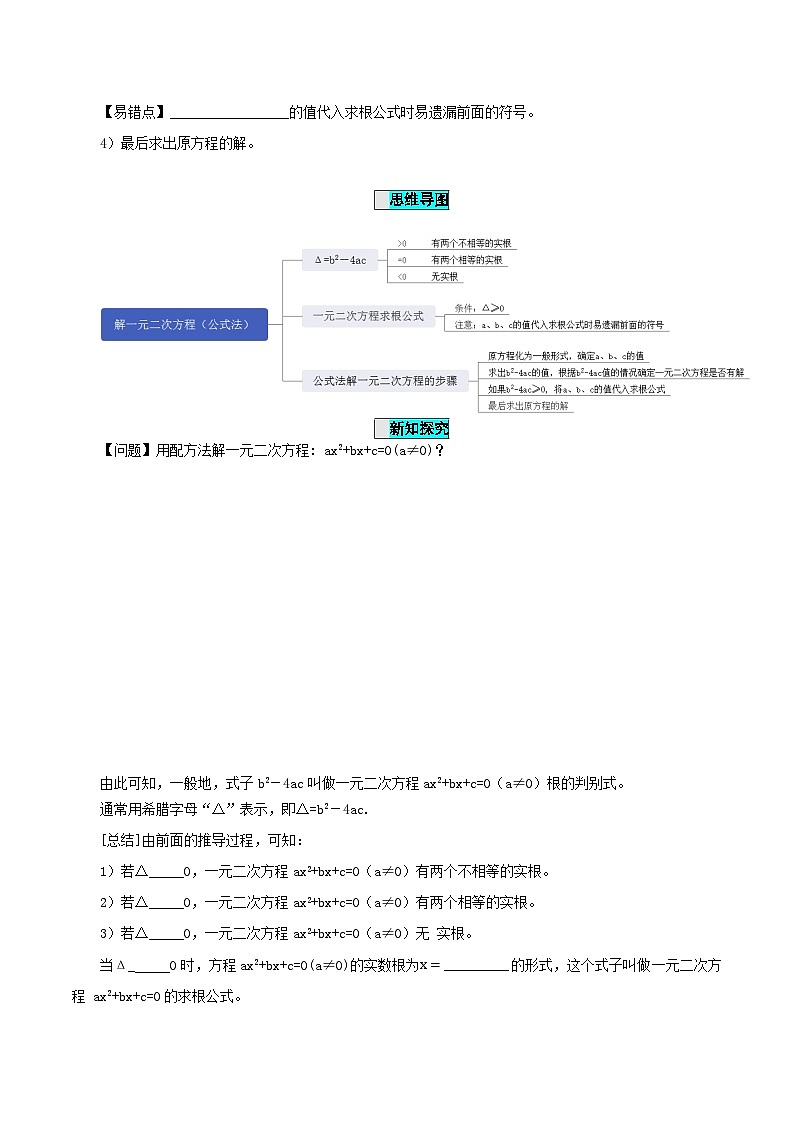
一般地,式子b2-4ac叫做一元二次方程ax2+bx+c=0(a≠0)根的判别式。
通常用希腊字母“Δ”表示,即Δ=b2-4ac.
由前面的推导过程,可知:1)若△>0,一元二次方程ax2+bx+c=0(a≠0)有两个不相等的实根。2)若△= 0,一元二次方程ax2+bx+c=0(a≠0)有两个相等的实根。3)若△<0,一元二次方程ax2+bx+c=0(a≠0)无 实根。
注意:a,b,c的符号
例1 3)5x2-3x=x+1 4)x2+17=8x
【提问】简述通过公式法解一元二次方程的步骤。
3)如果b2-4ac≥0, 将a、b、c的值代入求根公式。 【易错点】a、b、c的值代入求根公式时易遗漏前面的符号。
1)将原方程化为一般形式,确定a、b、c的值 【小技巧】若系数是分数通常将其化为整数,方便计算。
2)求出b2-4ac的值,根据b2-4ac值的情况确定一元二次方程是否有解。
4)最后求出原方程的解。
例3 求本章引言中的问题,雕像下部高度x(m)满足方程x2 +2x-4=0
2 下列一元二次方程中,有两个不相等实数根的是( )A.x2+6x+9=0 B.x2=xC.x2+3=2x D.(x﹣1)2+1=0
【详解】A. △=62-4×9=36-36=0,方程有两个相等实数根;B .原式变形为x2-x=0,∴△=(-1)2-4×1×0=1>0.方程有两个不相等实数根;C .原式变形为x2-2x+3=0,∴△=(-2)2-4×1×3=-8<0,方程无实根;D .原式变形为(x-1)2=-1,则方程无实根;故选B.
【详解】A.∵△=4-4×1×0=4>0,∴方程有两个不相等的实数根,故本选项不符合题意;B.∵△=16-4×1×(-1)=20>0,∴方程有两个不相等的实数根,故本选项不符合题意;C.∵△=25-4×3×2=1>0,∴方程有两个不相等的实数根,故本选项不符合题意;D.∵△=16-4×2×3=-8<0,∴方程没有实数根,故本选项正确;故选:D.
【详解】解:∵关于x的方程x2-2x+2m-1=0有实数根,∴b2-4ac=4-4(2m-1)≥0,解得:m≤1,∵m为正整数,∴m=1,∴此时二次方程为:x2-2x+1=0,则(x-1)2=0,解得:x1=x2=1.
1. 本节课学习,你有哪些收获?请你用自己的语言描述公式法解一元二次方程的基本步骤吗?2. 通过本节课的学习,你领悟到哪些数学思想方法?
P16:习题21.2:第4题(1)(4) 第5题(2)(3)(6) [选做]第13题
初中数学人教版九年级上册25.1.2 概率完美版教学ppt课件: 这是一份初中数学人教版九年级上册<a href="/sx/tb_c24925_t3/?tag_id=26" target="_blank">25.1.2 概率完美版教学ppt课件</a>,文件包含2512概率pptx、2512概率教学设计docx、2512概率导学案docx等3份课件配套教学资源,其中PPT共25页, 欢迎下载使用。
人教版九年级上册第二十四章 圆24.1 圆的有关性质24.1.1 圆优质教学课件ppt: 这是一份人教版九年级上册<a href="/sx/tb_c88761_t3/?tag_id=26" target="_blank">第二十四章 圆24.1 圆的有关性质24.1.1 圆优质教学课件ppt</a>,文件包含2411圆pptx、2411圆教学设计docx、2411圆导学案docx等3份课件配套教学资源,其中PPT共31页, 欢迎下载使用。
初中人教版21.2.3 因式分解法优秀教学ppt课件: 这是一份初中人教版<a href="/sx/tb_c88755_t3/?tag_id=26" target="_blank">21.2.3 因式分解法优秀教学ppt课件</a>,文件包含2123解一元二次方程因式分解法pptx、2123解一元二次方程因式分解法教学设计docx、2123解一元二次方程因式分解法导学案docx等3份课件配套教学资源,其中PPT共27页, 欢迎下载使用。














