初中数学人教版九年级上册21.3 实际问题与一元二次方程获奖教学课件ppt

这是一份初中数学人教版九年级上册21.3 实际问题与一元二次方程获奖教学课件ppt，文件包含213实际问题与一元二次方程传播问题和变化率问题pptx、213实际问题与一元二次方程传播问题和变化率问题教学设计docx、213实际问题与一元二次方程传播问题和变化率问题导学案docx等3份课件配套教学资源，其中PPT共29页， 欢迎下载使用。

1.根据实际问题中的数量关系，正确列出一元二次方程。2.通过列方程解应用题体会一元二次方程在实际生活中的应用，经历将实际问题转化为数学问题的过程，提高数学应用意识。
【提问】已经学过了哪些解一元二次方程的方法?
(x+m)2=n (n≥0)
(x-x1)(x-x2)=0
【提问】回顾列方程解决实际问题的基本步骤?
1）审：分清已知未知，明确数量关系；
5）验：根据实际验结果；
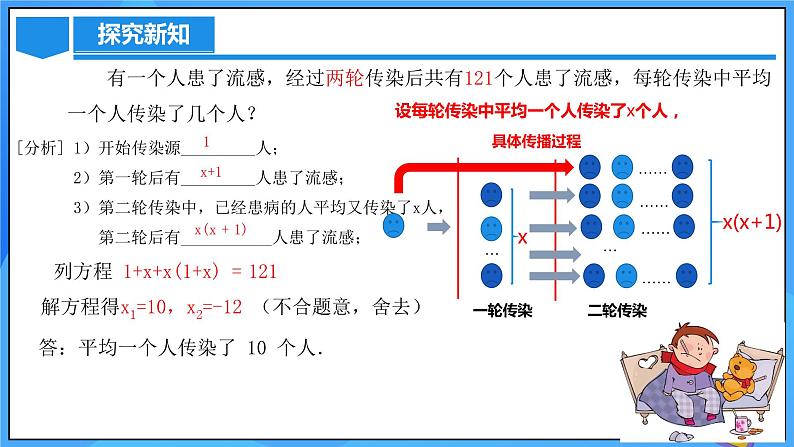
有一个人患了流感，经过两轮传染后共有121个人患了流感，每轮传染中平均一个人传染了几个人？
[分析] 1）开始传染源_________人； 2）第一轮后有_________人患了流感； 3）第二轮传染中，已经患病的人平均又传染了x人， 第二轮后有___________人患了流感；
设每轮传染中平均一个人传染了x个人，
列方程 1+x+x(1+x) = 121
　　答：平均一个人传染了 10 个人．
解方程得x1=10，x2=-12 （不合题意，舍去）
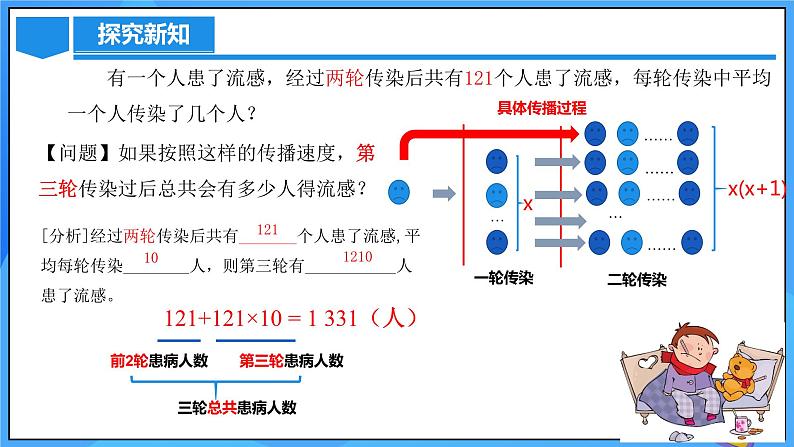
【问题】如果按照这样的传播速度，第三轮传染过后总共会有多少人得流感？
[分析]经过两轮传染后共有_______个人患了流感,平均每轮传染________人，则第三轮有___________人患了流感。
121+121×10 = 1 331（人）
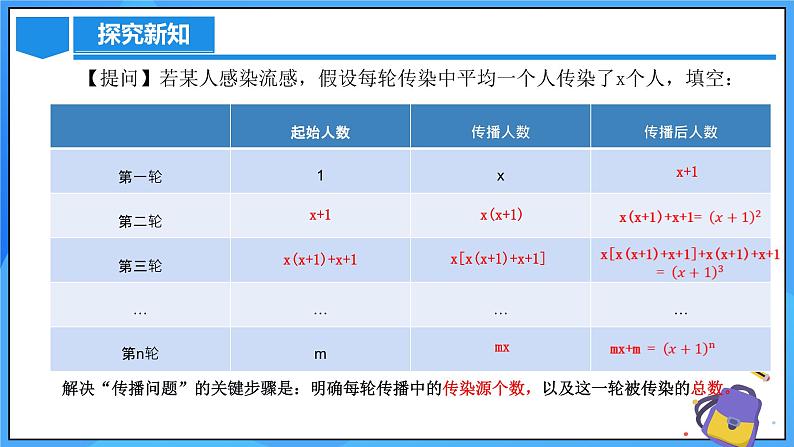
【提问】若某人感染流感，假设每轮传染中平均一个人传染了x个人，填空：
x[x(x+1)+x+1]
解决“传播问题”的关键步骤是：明确每轮传播中的传染源个数，以及这一轮被传染的总数。
例1 某种电脑病毒传播速度非常快，如果一台电脑被感染，经过两轮感染后就会有144台电脑被感染．请你用学过的知识分析，每轮感染中平均一台电脑会感染几台电脑？若病毒得不到有效控制，3轮感染后，被感染的电脑会不会超过1700台？
例2 某种流感病毒，若有一人患了这种流感，则在每轮传染中一人将平均传染x人．(1)现有一人患上这种流感，求第一轮传染后患病的人数（用含x的代数式表示）；(2)在进入第二轮传染前，有两位患者被及时隔离并治愈，问第二轮传染后患病的人数会有21人吗？
1．有一个人患了流感，经过两轮传染后有若干人被传染上流感．假设在每轮的传染中平均一个人传染了x个人．(1)第二轮被传染上流感人数是______；（用含x的代数式表示）(2)在进入第二轮传染之前，如果有4名患者被及时隔离（未治愈），经过两轮传染后是否会有63人患病的情况发生，并说明理由．
2. 学生会要组织“西实杯”篮球赛，赛制为单循环形式（每两队之间都赛一场）．（1）如果有4支球队参加比赛，那么共进行______场比赛；（2）如果全校一共进行36场比赛，那么有多少支球队参加比赛？
3 某种植物的主干长出若干数目的支干，每个支干又长出同样数目的小分支，主干、支干和小分支的总数是91，每个支干长出多少个小分支？
解：设每个支干长出 x 个小分支， 则 1 + x + x2 = 91解方程，得x1 = 9，x2 = -10（不合题意，舍去） 答：每个支干长出 9 个小分支
1．某农户的小麦产量年平均增长率为 x，第一年的产量为 50 000 kg，第二年的产量为____________ kg，第三年的产量为______________ kg．
50 000(1 + x )
2．某粮食厂2021年面粉产量为a吨，如果在以后两年平均减产的百分率为 x，那么预计 2022年的产量将是_________吨．2023年的产量将是__________吨．
两年前生产1t甲种药品的成本是5000元，生产1t乙种药品的成本是6000元，随着生产技术的进步，现在生产1t甲种药品的成本是3000元，生产1t乙种药品的成本是3600元，哪种药品成本的年平均下降率较大？
【提问】什么是下降额？下降率如何计算？
下降额=下降前的量-下降后的量
增长额=增长后的量-增长前的量
【提问】什么是增长额？增长率如何计算？
乙种药品成本的年平均下降额为（6000-3600）÷2=1200（元）．
甲种药品成本的年平均下降额为（5000-3000）÷2=1000（元），
显然，乙种药品的年平均下降额较大，但是年平均下降额（元）不等同于年平均下降率（百分率）。
解：设甲种药品成本的年平均下降率为 x　　一年后甲种药品成本为____________元，　　两年后甲种药品成本为____________元．
答：甲种药品成本的年平均下降率为22.5%
【补充】下降率是用减少的数除以原数，则所得结果必定小于1，因此不能大于或等于1。
解：设乙种药品成本的年平均下降率为 y　　一年后乙种药品成本为____________元，　　两年后乙种药品成本为____________元．
答：乙种药品成本的年平均下降率为22.5%
【问题】经过计算，你能得出什么结论？
【问题】成本下降额大的药品，它的成本下降率一定也大吗？
【问题】应怎样全面地比较几个对象的变化状况？
　成本下降额表示绝对变化量，成本下降率表示相对变化量，两者兼顾才能全面比较对象的变化状况。
两种药品成本的年平均下降率相等
成本下降额较大的产品，其成本下降率不一定较大。
【详解】（1）设每个月生产成本的下降率为x，根据题意得：400（1﹣x）2=361，解得：x1=0.05=5%，x2=1.95（不合题意，舍去）．答：每个月生产成本的下降率为5%；（2）361×（1﹣5%）=342.95（万元），答：预测4月份该公司的生产成本为342.95万元．
例3 某公司今年1月份的生产成本是400万元，由于改进技术，生产成本逐月下降，3月份的生产成本是361万元．假设该公司2、3、4月每个月生产成本的下降率都相同．（1）求每个月生产成本的下降率；（2）请你预测4月份该公司的生产成本．
1.2021年是中国共产党建党100周年，全国各地积极开展“弘扬红色文化，重走长征路”主题教育学习活动，我市“红二方面军长征出发地纪念馆”成为重要的活动基地．据了解，今年3月份该基地接待参观人数10万人，5月份接待参观人数增加到12.1万人．（1）求这两个月参观人数的月平均增长率；（2）按照这个增长率，预计6月份的参观人数是多少？
4．（2023·湖南郴州真题）随旅游旺季的到来，某景区游客人数逐月增加，2月份游客人数为1.6万人，4月份游客人数为2.5万人．(1)求这两个月中该景区游客人数的月平均增长率；(2)预计5月份该景区游客人数会继续增长，但增长率不会超过前两个月的月平均增长率．已知该景区5月1日至5月21日已接待游客2.125万人，则5月份后10天日均接待游客人数最多是多少万人？
5．（2021·山东东营真题）“杂交水稻之父”——袁隆平先生所率领的科研团队在增产攻坚第一阶段实现水稻亩产量700公斤的目标，第三阶段实现水稻亩产量1008公斤的目标．（1）如果第二阶段、第三阶段亩产量的增长率相同，求亩产量的平均增长率；（2）按照（1）中亩产量增长率，科研团队期望第四阶段水稻亩产量达到1200公斤，请通过计算说明他们的目标能否实现．
1. 本节课学习，你有哪些收获？请你用自己的语言简述一元二次方程解应用题的步骤？2. 你知道本节课研究“传播问题”的基本特征吗？解决此类问题的关键步骤是什么？
“传播问题”的基本特征：以相同的速度逐轮传播。解决此类问题的关键步骤：明确每轮传播中的传染源个数，以及这一轮被传染的总数。
P25：复习题21：第7题、第9题、第10题