人教版数学九年级上册 第二十一章 一元二次方程 单元复习（课件）

这是一份人教版数学九年级上册 第二十一章 一元二次方程 单元复习（课件），共60页。

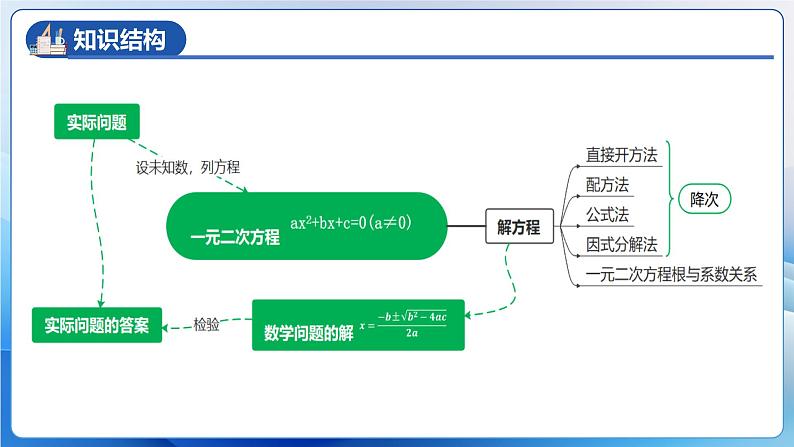
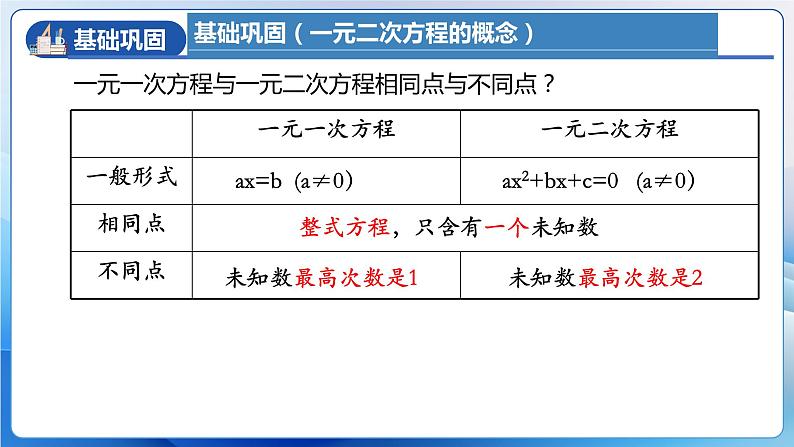
章节复习第二十一章 一元二次方程重点难点章节简介基础巩固题型演练学习目标1)了解一元二次方程及其相关概念，会用配方法、公式法、分解因式法解一元二次方程，并在解一元二次方程的过程中体会转换、降次等数学思想。　　2)通过根的判别式判断一元二次方程的情况，了解根与系数的关系。3)能够利用一元二次方程解决有关实际问题，能根据具体问题的实际意义检验结果的合理性，进一步培养学生分析问题、解决问题的意识和能力。　　本章重点内容：1.理解与掌握一元二次方程及其有关的概念。2.用配方法、公式法、因式分解法解一元二次方程。3.利用一元二次方程解决实际问题。　本章难点内容：1.理解用根的判别式判别根的情况。2.一元二次方程求根公式的推导。3.一元二次方程根与系数的关系。 解一元二次方程方法为本章基础内容，它的计算量相对较大，对正确率要求比较高，要求根据方程的结构，选用合适的方法解方程。大题通常考查利用一元二次方程解决实际问题和一元二次方程根与系数关系，利用一元二次方程解决实际问题难点在于找等量关系，正确列出方程并求解，从而解决实际问题。利用根与系数的关系求代数式的值，难度较大，需要多加练习，灵活运用根与系数关系变形求解！ 只含有_______未知数（元），并且未知数最高次数是_____，等号两边都是________，这样的方程叫一元二次方程。一个2整式ax 2 + bx + c = 0（a≠0）一元二次方程的一般形式为___________________________________。二次项一次项常数项二次项系数一次项系数【提问】为什么强调a≠0一元一次方程与一元二次方程相同点与不同点？ax=b (a≠0）ax2+bx+c=0 (a≠0）整式方程，只含有一个未知数未知数最高次数是1未知数最高次数是2一般地，对于方程x2＝p ①，1)当p＞0时，根据平方根的意义，方程①有两个____________的实数根______________________；2)当p＝0时，方程①有两个______的实数根_____________；3)当p＜0时，因为对于任意实数x，都有x2____0，所以方程① _______实数根。不相等相等x1＝x2＝0无≥  将方程通过配成____________形式来解一元二次方程的方法，叫做配方法。配方是为了___________，把一个一元二次方程转化成______一元一次方程来解。用配方法解一元二次方程的关键：将一元二次方程配成完全平方形式。完全平方降次两个不能直接开平方解的一元二次方程可以直接开平方解的一元二次方程变形为通过配方法解一元二次方程的步骤: 一般地，如果一个一元二次方程通过配方转化成(x＋n)2＝p ①的形式，那么就有：1)当p＞0时，根据平方根的意义，方程①有两个________________的实数根______________________；2)当p＝0时，方程①有两个________________的实数根______________________；3)当p＜0时，因为对于任意实数x，都有(x＋n)2____0，所以方程①_______实数根。不相等相等x1＝x2＝-n无≥ 一般地，式子b2－4ac叫做一元二次方程ax2+bx+c=0（a≠0）根的判别式。判别式概念：判别式表示：通常用希腊字母“Δ”表示，即Δ=b2－4ac.由前面的推导过程，可知：1）若△＞0，一元二次方程ax2+bx+c=0（a≠0）有____________________________的实根。1）若△= 0，一元二次方程ax2+bx+c=0（a≠0）有____________________________的实根。1）若△＜0，一元二次方程ax2+bx+c=0（a≠0） ____________________________实根。两个不相等两个 相等无   代入求根公式公式法解一元二次方程的步骤:3）如果b2-4ac≥0, 将a、b、c的值代入求根公式。 【易错点】a、b、c的值代入求根公式时易遗漏前面的符号。1）将原方程化为一般形式，确定a、b、c的值 【小技巧】若系数是分数通常将其化为整数，方便计算。2）求出b2-4ac的值，根据b2-4ac值的情况确定一元二次方程是否有解。4）最后求出原方程的解。 先因式分解，使一元二次方程转化为____________________的形式，从而实现________，这种解一元二次方程的方法叫做因式分解法。两个一次式乘积等于0降次通过因式分解法解一元二次方程的步骤:1.移项。使一元二次方程等式右边为0；2.分解。把左边运用因式分解法化为两个一次因式相乘的形式；3.赋值。令每个因式等于0，得到两个一元一次方程；4.求解。解这两个一元一次方程，最后得到方程的解。归纳：左分解，右化零，两因式，各求解。解一元二次方程的方法解一元二次方程的基本思路是：将二次方程化为一次方程，即降次。 【易错点】使用韦达定理的前提条件：1) 先把方程化为一般式。 2) Δ≥0。比的相反数比       利用一元二次方程解决实际问题：1）传播问题：明确每轮传播中的___________个数，以及这一轮被传染的__________．2) 增长率问题： ①如果增长率问题中的基数为a，平均增长率为x，则第一次增长后的数量为 ____________，第二次增长后的数量为____________． ②如果下降率问题中的基数为a，平均下降率为x，则第一次下降后的数量为 __________，第二次下降后的数量为___________．3）几何问题：①常见几何____________是等量关系。 ②解决课本封面、小路宽度常采用____________列方程。传染源总数a(1＋x)a(1＋x)2a(1－x)a(1－x)2周长面积图形平移利用一元二次方程解决实际问题：4) 数字问题： ①若个位数字为a，十位数字为b，百位数字为c，则十位数字表示为____________. 百位数字表示_____________. ②日历中的某个日期，左右相差___________，上下相差___________.5）利润问题：单件利润=___________,总利润=________________6) 表格问题：理解题干内容，从题干中获取信息。7）动点问题：在动点中观察图形的变化情况，需理解动点在图形不同位置情况，才 能做好计算推理过程。在变化中找到不变的性质是解决动点问题的基本思路。100c+10b+a10b+a17售价-进价单件利润×销量 1）用直接开平方法、配方法、公式法或因式分解法解一元二次方程。2）一元二次方程根的判别式，有两种考查方式： ①给出一元二次方程，求方程的根的情况。 ②给出带有参数的一元二次方程和根的情况，求参数的取值范围。3）一元二次方程的根与系数的关系，主要考查方式： ①不解方程，判断两个数是不是一元二次方程的两个根； ②已知方程及方程的一个根，求另一个根及未知数； ③不解方程求关于根的式子的值，如求x12+x22等； ④判断两根的符号；⑤求作新方程；⑥由给出的两根满足的条件，确定字母的取值。4）列一元二次方程解决实际问题，以实际生活为背景，命题比较广泛（常见的题型是增长率/传播问题）. 1．已知关于x的方程(2k＋1)x2＋4kx＋k－1＝0，问：（1）k为何值时，此方程是一元一次方程？（2）k为何值时，此方程是一元二次方程？并写出这个一元二次方程的二次项系数、一次项系数及常数项．  【详解】①②③⑤都是或可变形为x2=a（a≥0）；ax2=b（a，b同号且a≠0）；（x+a）2=b（b≥0）；a（x+b）2=c，而这四种形式都可用直接开平方法，故选D．1. 用直接开平方法解下列方程：（1）（x﹣2）2=3； （2）2（x﹣3）2=72；（3）9（y+4）2﹣49=0； （4）4（2y﹣5）2=9（3y﹣1）2．            【详解】∵(x2﹣x)2﹣4(x2﹣x)﹣12＝0∴(x2﹣x+2)(x2﹣x﹣6)＝0，∴x2﹣x+2＝0或x2﹣x﹣6＝0，∴x2﹣x＝﹣2或x2﹣x＝6；当x2﹣x＝﹣2时，x2﹣x+2＝0，∵b2﹣4ac＝1﹣4×1×2＝﹣7＜0，∴此方程无实数解；当x2﹣x＝6时，x2﹣x+1＝7，故选A．                1.矩形面积为864平方步，宽与长共60步，问长与宽各多少步．利用所学知识，可求出长与宽分别是_______________2.组织一次排球邀请赛，参赛的每两个队都要比赛一场.根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛，则比赛组织者应邀请_________个队参赛？ 【详解】解：设长为x步，则宽为（60−x）步，依题意，得：x（60−x）＝864，解得：x1＝36，x2＝24，答：长与宽分别是36步，24步，    1．“新冠肺炎”防治取得战略性成果．若有一个人患了“新冠肺炎”，经过两轮传染后共有25个人患了“新冠肺炎”，则每轮传染中平均一个人传染了_________人． 【详解】设十位上的数字为x，则个位上的数字为（x﹣4）．可列方程为：x2+（x﹣4）2＝10x+（x﹣4）﹣4解得：x1＝8，x2＝1.5（舍），∴x﹣4＝4，∴10x+（x﹣4）＝84．答：这个两位数为84．故答案为：842．已知一个两位数，个位上的数字比十位上的数字小4，且个位上的数字与十位上的数字的平方和比这个两位数小4，则这个两位数是___．     一元二次方程是初中数学的重要内容，在历次中考中均占重要地位。根据近几年各地中考发现，考查题型不固定，基础题、中档题、难题均有涉及，解答题中通常会出现解一元二次方程的题型，这类题型较为基础，应用题会出现一元二次方程、一元二次方程组，不等式综合命题，而且一元二次方程常与二次函数、解直角三角形、圆等知识综合命题作为中考压轴题出现。                      14．（2022年江苏省泰州市中考数学真题）如图，在长为50 m，宽为38 m的矩形地面内的四周修筑同样宽的道路，余下的铺上草坪．要使草坪的面积为1260 m2，道路的宽应为多少？【详解】解：设道路的宽应为x米，由题意得(50-2x)×(38-2x)=1260解得：x1=4，x2=40(不符合题意，舍去)答：道路的宽应为4米．    课程结束