








初中第二十二章 二次函数22.1 二次函数的图象和性质22.1.2 二次函数y=ax2的图象和性质优质教学课件ppt
展开【提问1】画一个函数图象需要哪些步骤?【提问2】画一次函数y=3x+2的图象?【提问3】一次函数的图象是什么形状?二次函数的图象是是什么形状?
一次函数的图象是一条直线
本节课我们学习二次函数y=ax2的图象和性质
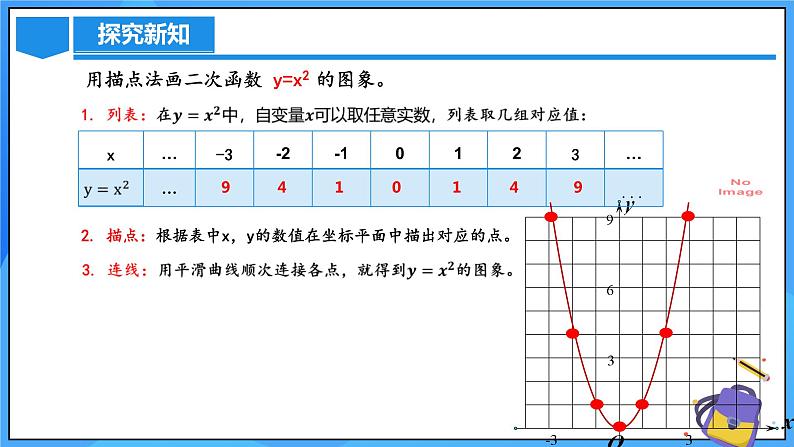
用描点法画二次函数 y=x2 的图象。
2. 描点:根据表中x,y的数值在坐标平面中描出对应的点。
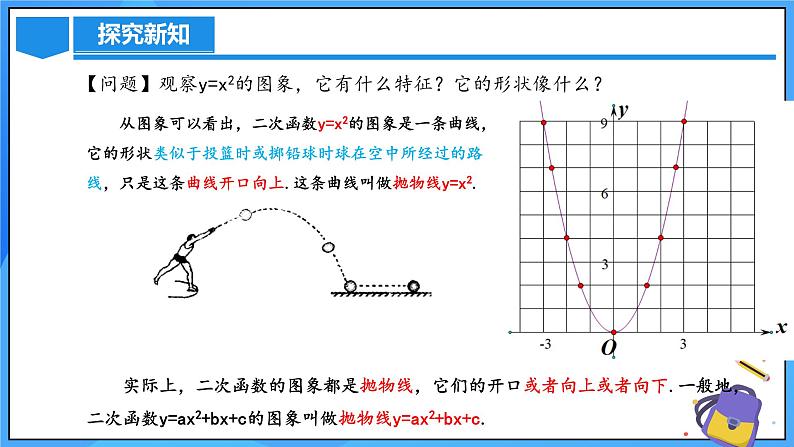
【问题】观察y=x2的图象,它有什么特征?它的形状像什么?
从图象可以看出,二次函数y=x2的图象是一条曲线,它的形状类似于投篮时或掷铅球时球在空中所经过的路线,只是这条曲线开口向上.这条曲线叫做抛物线y=x2.
实际上,二次函数的图象都是抛物线,它们的开口或者向上或者向下.一般地,二次函数y=ax2+bx+c的图象叫做抛物线y=ax2+bx+c.
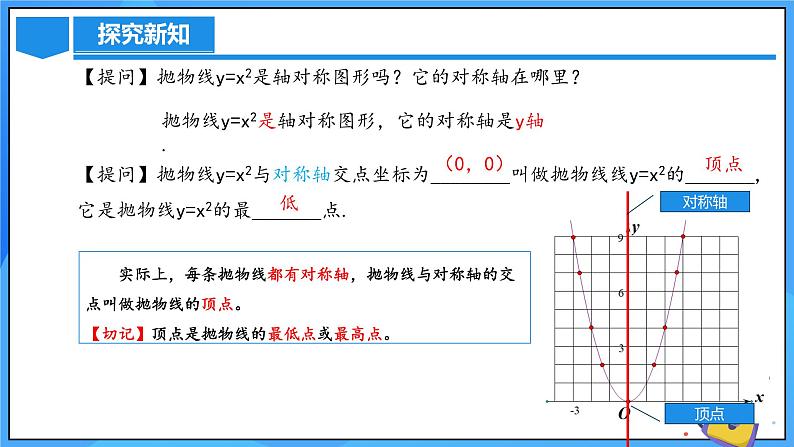
【提问】抛物线y=x2是轴对称图形吗?它的对称轴在哪里?
【提问】抛物线y=x2与对称轴交点坐标为________叫做抛物线线y=x2的_______,它是抛物线y=x2的最_______点.
抛物线y=x2是轴对称图形,它的对称轴是y轴.
实际上,每条抛物线都有对称轴,抛物线与对称轴的交点叫做抛物线的顶点。【切记】顶点是抛物线的最低点或最高点。
【提问】观察y=x2的图象,讨论x与y的变化趋势?
1)开口都向上(a>0) ,对称轴都是y轴。
2)当x<0时,y随x增大而减小; 当x>0时,y随x增大而增大。
3)顶点是原点(最小值)。
4)a值越大抛物线开口越小。
(提示:从开口方向、对称轴、顶点、增减性等方面思考)
【结论】一般地,当a>0时,抛物线y=ax2的开口向上,对称轴是y轴,顶点是原点,顶点是抛物线的最低点,a越大,抛物线的开口越小.
1)开口都向下(a<0) ,对称轴都是y轴。
2)当x<0时,y随x增大而增大; 当x>0时,y随x增大而减小。
3)顶点是原点(最大值)。
4)a值越小抛物线开口越小。
【结论】一般地,当a<0时,抛物线y=ax2的开口向下,对称轴是y轴,顶点是原点,顶点是抛物线的最高点,a越小,抛物线的开口越小.
【问题】对比抛物线y=x2和y=-x2,它们关于x轴对称吗?一般地,抛物线y=ax2和y=-ax2呢?
二次项系数互为相反数,则它们关于x轴对称,且抛物线开口方向相反,大小相同.
当x<0时,y随x的增大而减小;当x>0时,y随x的增大而增大.
当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小.
当x=0时,y最小=0
当x=0时,y最大=0
【详解】解:∵抛物线y=ax2与y=2x2的形状相同, ∴|a|=2,∴a=±2.故答案为±2.
【提问】有没有其它求解方法?
二次函数y=ax2 中比较函数值的大小的方法:
例5.二次函数的图像如图所示,则m ____ n(填“>”或“<”).
1.如图,⊙O的半径为2,C1是函数y=2x2的图象,C2是函数y=-2x2的图象,则图中阴影部分的面积为_______. 2.如图,正方形的边长为2,图中阴影部分的面积为________.
3.已知函数y=(k﹣2)xk2-4k+5是关于x的二次函数,求:(1)满足条件的k的值;(2)当k为何值时,抛物线有最高点?求出这个最高点,这时,x为何值时,y随x的增大而增大?(3)当k为何值时,函数有最小值?最小值是多少?这时,当x为何值时,y与x的增大而减小?
【详解】解:∵二次函数y=ax2的图象开口向上,∴a>0;又∵直线y=ax-1与y轴负半轴相交,∴y=ax-1经过的象限是第一、三、四象限.故选:D.
1.如何画出函数y=ax2的图象?2.函数y=ax2具有哪些性质?3. 谈谈你对本节课学习的体会?4.通过本节课的学习,你想继续探究的知识是什么?
P32:课后练习P41:习题22.1第3题和第4 题
人教版九年级上册22.1.3 二次函数y=a(x-h)2+k的图象和性质精品教学ppt课件: 这是一份人教版九年级上册<a href="/sx/tb_c95448_t3/?tag_id=26" target="_blank">22.1.3 二次函数y=a(x-h)2+k的图象和性质精品教学ppt课件</a>,文件包含2213二次函数yax2+k的图象和性质pptx、2213二次函数yax2+k的图象和性质教学设计docx、2213二次函数yax2+k的图象和性质导学案docx等3份课件配套教学资源,其中PPT共38页, 欢迎下载使用。
初中数学人教版九年级上册22.1.2 二次函数y=ax2的图象和性质优质课ppt课件: 这是一份初中数学人教版九年级上册22.1.2 二次函数y=ax2的图象和性质优质课ppt课件,文件包含人教版初中数学九年级上册2212二次函数yax2的图象和性质课件PPTpptx、人教版初中数学九年级上册2212二次函数yax2的图象和性质教案docx、人教版初中数学九年级上册2212二次函数yax2的图象和性质分层练习docx、人教版初中数学九年级上册2212二次函数yax2的图象和性质预习案docx等4份课件配套教学资源,其中PPT共38页, 欢迎下载使用。
人教版九年级上册22.1.1 二次函数精品ppt课件: 这是一份人教版九年级上册22.1.1 二次函数精品ppt课件,共18页。PPT课件主要包含了学习目标,新知学习,y2x2,y-2x2,课堂小结,单击此处添加标题,点击播放,位置开口方向,对称性,顶点最值等内容,欢迎下载使用。














