人教版数学九年级上册 第二十三章 旋转（单元解读）课件

这是一份人教版数学九年级上册 第二十三章 旋转（单元解读）课件，共14页。

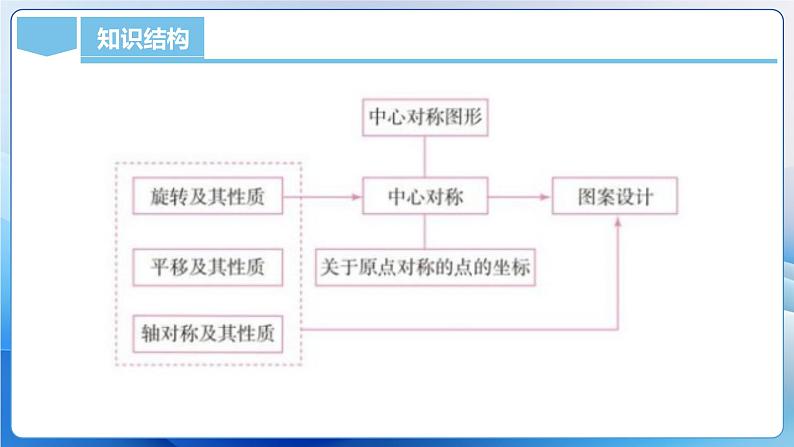
单 元 解 读第二十三章 旋转课标解读内容分析单元目标知识结构课时安排《义务教育数学课程标准（2022年版）》对旋转相关内容提出的要求如下:①通过具体实例认识平面图形关于旋转中心的旋转。探索它的基本性质：一个图形和旋转得到的图形中，对应点到旋转中心距离相等，两组对应点分别与旋转中心连线所成的角相等。②了解中心对称、中心对称图形的概念，探索它们的基本性质：成中心对称的两个图形中，对应点的连线经过对称中心，且被对称中心平分。③探索线段、平行四边形、正多边形、圆的中心对称性质。④认识并欣赏自然界和现实生活中的中心对称图形。 旋转是九年级第三章所学内容，它是一种全等变形，其主要考点有中心对称图形，旋转作图等。判断中心对称图形是一个高频考点。在考试中可以把试卷倒过来看，如果正看与倒看图形是一模一样，就可以确定是中心对称图形。旋转需要掌握的第二个考点就是旋转的坐标变化，在解决相关问题时，一定要先弄清楚图形的性质，再弄清楚旋转中心、旋转方向和旋转角度。第三个考点为旋转性质与几何证明，旋转是全等变形，利用全等三角形的性质可以把具有数量关系，但是位置上比较零散的线段集中到一起，方便解决问题。1 了解图形的旋转的有关概念并理解它的基本性质。2 了解中心对称和中心对称图形的概念并理解它的基本性质。3 掌握关于原点对称的两点的关系并应用。本章重点内容：1）理解并掌握图形旋转和中心对称基本性质。　　2) 两个点关于原点对称时，它们坐标之间的关系。本章难点内容：1) 图形旋转的基本性质的归纳与运用。2) 中心对称的基本性质的归纳与运用。命题趋势： 旋转是初中几何的一个重难点，而且旋转常作为中考命题者重点考虑的命题方向。由旋转产生的图形与关系非常多，且灵活多变，可以考查的知识点非常多，例如考查三角形全等与相似、四边形、圆，勾股定理等，更能考查学生综合能力，常以压轴题的形式出现。第一课时图形的旋转内容解析 通过旋转的学习，结合平移和轴对称的相关知识，学生将更加系统地认识图形变换的研究过程，对图形变换的思想体会得更加深入．旋转有三条性质：1.对应点到旋转中心的距离相等. 2.对应点与旋转中心所连线段的夹角等于旋转角. 3.旋转前、后的图形全等.利用旋转前、后的图形全等，我们可以画简单图形旋转后的图形.第二课时 中心对称内容解析 本节课我们学习中心对称的概念及性质，先让学生从旋转的角度观察两个图形之间的关系，类比旋转得出中心对称的概念，渗透了从一般到特殊的数学思想方法. 通过操作、观察、归纳得出中心对称的性质，体会由具体到抽象认识问题的过程，并能运用中心对称的性质画出一个图形关于某一点的对称图形.第三课时 中心对称图形内容解析 本节课从两个简单的中心对称图形实例入手，让学生类比中心对称得出中心对称图形的概念，渗透从一般到特殊的数学思想方法，并会判断一个图形是否为中心对称图形.在此基础上，通过对比中心对称和中心对称图形的概念和性质，加深理解知识之间的区别与联系.第四课时 关于原点对称点的坐标内容解析 本节课在学生学习平移、轴对称在平面直角坐标系中坐标特点的基础上，进一步研究关于原点对称的两点坐标间的关系，并利用这一关系解决一些问题.第五课时课题学习 图案设计内容解析 本节课我们学习利用平移、轴对称和旋转这些图形变换中的一种或组合进行图案设计，有利于学生认识图形间运动变化和联系，培养学生的审美能力.学情分析： 本章是在学生已经学习了平移和轴对称的基础上来学习的，针对九年级学生，逻辑思维正在从经验型逐步向理论型发展，观察能力、记忆能力和想象能力也在迅速发展，他们有强烈的独立思考、自主探索的愿望，这些对本章的学习都会有帮助.但旋转是三种变换中难度较大的一种，图形也比较复杂，因此，学生对旋转图形的形成过程的理解仍会有一定的困难.教学中通过类比会对旋转学习有帮助.课程结束