








数学九年级上册23.2.2 中心对称图形完整版教学ppt课件
展开1 了解中心对称图形的概念,会判断一个图形是否为中心对称图形.2 理解中心对称和中心对称图形的联系与区别.
【问题一】中心对称的概念?【问题二】中心对称的性质?
把一个图形绕某一个点旋转180º,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称.1)这个点叫做对称中心.2)这两个图形中的对应点叫做关于中心的对称点.
1)中心对称的两个图形,对称点所连线段经过对称中心,而且被对称中心所平分.2)中心对称的两个图形是全等形.
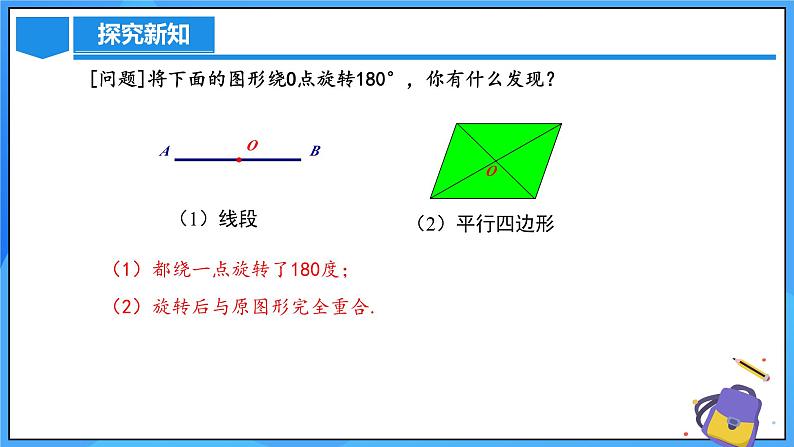
[问题]将下面的图形绕O点旋转180°,你有什么发现?
(1)都绕一点旋转了180度;
(2)旋转后与原图形完全重合.
如果一个图形绕一个点旋转180°后,能和原来的图形互相重合,那么这个图形叫做中心对称图形;这个点叫做它的对称中心;互相重合的点叫做对称点.
[提问]1)你能指出图中的中心对称图形吗?2)你能指出图中的对称点吗?3)你能指出图中的对称中心吗?
点A与点C、点B与点D
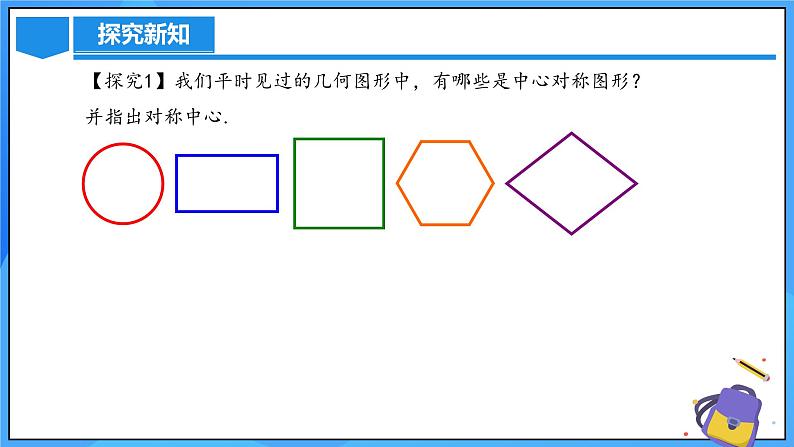
【探究1】我们平时见过的几何图形中,有哪些是中心对称图形? 并指出对称中心.
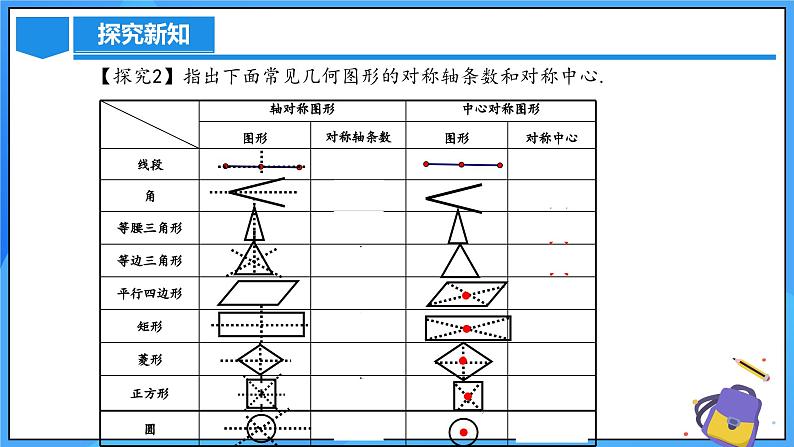
【探究2】指出下面常见几何图形的对称轴条数和对称中心.
【探究3】正三角形是中心对称图形吗?正方形呢?正五边形呢?正六边呢?你能发现什么规律?
边数为偶数的正多边形都是中心对称图形。
例1 判断下列图形是否为中心对称图形.若是画√,不是画×
1.观察图形,并回答下面的问题:1)哪些只是轴对称图形?2)哪些只是中心对称图形?3)哪些既是轴对称图形,又是中心对称图形?
A B C E S O W N I x Y Z
2 下列这些字母中有_____个是中心对称的图形。有____个是轴对称的图形。
3 下列这些数字中有_____个是中心对称的图形。有_____个是轴对称的图形。
4.在 ①平行四边形、 ②正方形、 ③等边三角形、 ④等腰梯形、 ⑤菱形、 ⑥圆、⑦正八边形这些图形中,既是轴对称图形又是中心对称图形的是_____________(填序号)5.下列四张扑克牌图案,属于中心对称图形的是( )
[问题]观察图形运动过程,并回答下面问题:1)中心对称图形的对称点连线都经过________2)中心对称图形的对称点连线被____________3) 简述中心对称图形的性质?
中心对称图形上每一对对应点连线都经过对称中心,并且被对称中心平分.
中心对称与中心对称图形的区别与联系:
例2 如图是一个中心对称图形,则此图形的对称中心为( )A.A点 B.B点 C.C点 D.D点
【详解】解:如图所示:点A与点C是对应点,点D与点E是对应点,线段AC与DE相交于点B,所以点B是对称中心.故选B.
1.如图,已知△ABC与△CDA关于点O成中心对称,过点O任作直线EF分别交AD,BC于点E,F,则下则结论:①点E和点F,点B和点D是关于中心O的对称点;②直线BD必经过点O;③四边形ABCD是中心对称图形;④四边形DEOC与四边形BFOA的面积必相等;⑤△AOE与△COF成中心对称.其中正确的个数为 ( )A.2B.3C.4D.5
【详解】△ABC与△CDA关于点O对称,则AB=CD、AD=BC,所以四边形ABCD是平行四边形,因此点O就是▱ABCD的对称中心,则有:(1)点E和点F;B和D是关于中心O的对称点,正确;(2)直线BD必经过点O,正确;(3)四边形ABCD是中心对称图形,正确;(4)四边形DEOC与四边形BFOA的面积必相等,正确;(5)△AOE与△COF成中心对称,正确;其中正确的个数为5个,故选D.
2.(1)指出下列旋转对称图形的最小旋转角,并在图中标明它的旋转中心O. (2)在上述几个图形中有没有中心对称图形?具体指明是哪几个?解:图形A的最小旋转角是 度,它 中心对称图形.图形B的最小旋转角是 度,它 中心对称图形.图形C的最小旋转角是 度,它 中心对称图形.图形D的最小旋转角是 度,它 中心对称图形.图形E的最小旋转角是 度,它 中心对称图形.
答案:60,是;72,不是;72,不是;120,不是;90,是.
3 下图是中心对称图形的一部分,请你补全它的另一部分.
提示:先根据图形中已知的对称点找对称中心,再根据中心对称图形的性质画出未知的对称点,最后顺次连接即可。
4.有一块方角形钢板如图所示,如何用一条直线将其分为面积相等的两部分.
5 用一条直线 m 将如图 1 的直角铁皮分成面积相等的两部分.图 2、图 3 分别是甲、乙两同学给出的作法,对于两人的作法判断正确的是( )A.甲正确,乙不正确 B.甲不正确,乙正确C.甲、乙都正确 D.甲、乙都不正确
【详解】如图:图形2中,直线m经过了大长方形和小长方形的对角线的交点,所以两旁的图形的面积都是大长方形和小长方形面积的一半,所以这条直线把这个图形分成了面积相等的两部分,即甲做法正确;图形3中,经过大正方形和图形外不添补的长方形的对角线的交点,直线两旁的面积都是大正方形面积的一半-添补的长方形面积的一半,所以这条直线把这个图形分成了面积相等的两部分,即乙做法正确.故选C.
1.(2023·江西·统考中考真题)下列图形中,是中心对称图形的是( )2.(2023·四川宜宾·统考中考真题)下列图案中,既是轴对称图形,又是中心对称图形的是( )
1.简述中心对称图形的概念与性质?2.简述中心对称和中心对称图形的联系与区别?
P69:习题23.2: 第2题,第5题,第8题.
初中数学人教版九年级上册25.1.2 概率完美版教学ppt课件: 这是一份初中数学人教版九年级上册<a href="/sx/tb_c24925_t3/?tag_id=26" target="_blank">25.1.2 概率完美版教学ppt课件</a>,文件包含2512概率pptx、2512概率教学设计docx、2512概率导学案docx等3份课件配套教学资源,其中PPT共25页, 欢迎下载使用。
数学25.1.1 随机事件完整版教学ppt课件: 这是一份数学<a href="/sx/tb_c88786_t3/?tag_id=26" target="_blank">25.1.1 随机事件完整版教学ppt课件</a>,文件包含2511随机事件pptx、2511随机事件教学设计docx、2511随机事件导学案docx等3份课件配套教学资源,其中PPT共26页, 欢迎下载使用。
人教版九年级上册第二十四章 圆24.1 圆的有关性质24.1.1 圆优质教学课件ppt: 这是一份人教版九年级上册<a href="/sx/tb_c88761_t3/?tag_id=26" target="_blank">第二十四章 圆24.1 圆的有关性质24.1.1 圆优质教学课件ppt</a>,文件包含2411圆pptx、2411圆教学设计docx、2411圆导学案docx等3份课件配套教学资源,其中PPT共31页, 欢迎下载使用。














