人教版数学九年级上册 第二十四章 圆（单元解读）课件

这是一份人教版数学九年级上册 第二十四章 圆（单元解读）课件，共23页。

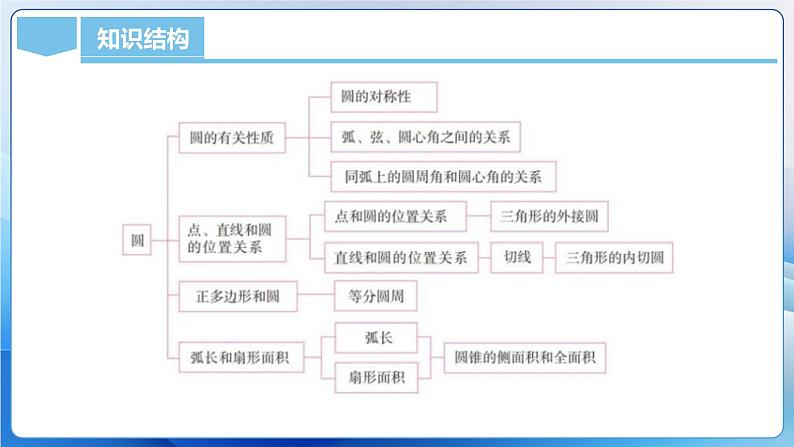
单 元 解 读第二十四章 圆课标解读内容分析单元目标知识结构课时安排《义务教育数学课程标准（2022年版）》对旋转相关内容提出的要求如下:①理解圆、弧、弦、圆心角、圆周角的概念,了解等圆、等弧的概念；探索并掌握点与圆的位置关系。　　②探索并证明垂径定理：垂直于弦的直径平分弦以及弦所对的两条弧。　　③探索圆周角与圆心角及其所对弧的关系，知道同弧（或等弧）所对的圆周角相等。了解并证明圆周角定理及其推论：圆周角等于它所对弧上的圆心角的一半；直径所对的圆周角是直角，90°的圆周角所对的弦是直径；圆内接四边形的对角互补。④了解三角形的内心与外心。⑤了解直线与圆的位置关系，掌握切线的概念。⑥能用尺规作图：过不在同一直线上的三点作圆；作三角形的外接圆、内切圆；作圆的内接正方形和内接正六边形。　　⑦能用尺规作图：过圆外一点作圆的切线。　　⑧探索并证明切线长定理：过圆外一点的两条切线长相等。　　⑨会计算圆的弧长、扇形的面积。　　⑩了解正多边形的概念及正多边形与圆的关系。 本章的主要内容有圆的概念及性质，垂直于弦的直径的性质，弧、弦、圆心角之间的关系及性质，圆周角的概念及性质，点和圆的位置关系，直线和圆的位置关系，圆和圆的位置关系，正多边形和圆的关系，弧长和扇形的面积，圆锥的侧面积和全面积。需理解圆心角、圆周角、弧、弦、相交、相切、相离，正多边形的半径、中心、边心距等概念，掌握垂径定理，切线的性质定理和判定定理，切线长定理等利用弧长公式、扇形面积公式，圆锥侧面积公式等进行计算。本章作为几何知识的总结，运用的知识具有综合性，在中考中所涉及的命题大多和圆的基本性质、与圆有关的位置关系、圆中的计算有关。1）理解圆及圆相关的概念.2) 会判断点、直线与圆之间的位置关系 .3) 理解圆的对称性及有关性质，会用垂径定理等解决有关问题.4) 了解圆的确定条件，了解三角形的外接圆以及圆的内接三角形相关的概念.5) 熟练掌握弧长和扇形面积公式及其它们的应用，理解圆锥的侧面展开图并熟练掌握圆锥的侧面积和全面积的计算．本章重点内容：1）理解圆及圆相关的概念.2) 理解圆的对称性及有关性质，会用垂径定理等解决有关问题.本章难点内容：1) 会判断点、直线与圆之间的位置关系 .2) 熟练掌握弧长和扇形面积公式及其它们的应用，理解圆锥的侧面展开图并熟练掌握圆锥的侧面积和全面积的计算．命题趋势： 圆作为中学数学阶段必学的知识内容之一，一直占据着重要的位置和作用。如在中考数学试卷中存在着大量与圆有关的题型，这些题目既能充分考查学生的几何综合应用能力，又能考查学生灵活运用知识的创新思维能力。纵观近几年全国各地中考题，圆的有关概念以及性质等一般以填空题、选择题的形式考查；圆的有关性质、如垂径定理、圆周角、切线的判定与性质等综合性问题的运用，一般以计算证明的形式考查；利用圆的知识与其他知识点如代数函数，方程等相结合作为中考压轴题将会占有非常重要的地位，另外与圆有关的实际应用题，阅读理解题，探索存在性问题仍是热门考题应引起注意。”圆”是几何题的重要考点，在中考中几乎年年出现，但是得分率却不高，因为题型复杂难度高.第一课时圆的内容解析 圆是继三角形、平行四边形、特殊四边形等基本图形后的又一个重要内容，在生活中有着广泛的应用.圆是平面几何中最基本的图形之一，在几何中有着重要的地位.本节课我们进一步从点的集合角度定义圆，渗透了集合的思想，理解并掌握圆的有关概念，如直径、半径、弧、弦、等弧、等圆等，为今后进一步学习圆的有关性质打好基础.第二课时垂直于弦的直径内容解析 圆有许多重要性质，其中最主要的性质是圆的对称性(轴对称性和旋转不变性)，它是探索其他性质的基础，垂径定理正是圆的轴对称性的具体体现．它是圆中证明线段相等、角相等以及垂直关系的重要依据，同时也为和圆有关的其它计算、证明、作图提供了重要的方法和依据，此外垂径定理也为研究弦、弧、圆心角定理提供了研究方法． 垂径定理的条件是：（1）过圆心（2）垂直于弦（3）平分弦（4）平分弦所对的优弧（5）平分弦所对的劣弧，已知五个条件中的两个就可推出其中三个，解题过程中应灵活运用该定理.第三课时弧、弦、圆心角内容解析 本节课我们首先探索圆的旋转不变性，在学生掌握此性质的基础，我们继续探索弧、弦、圆心角之间的关系.它是继垂径定理后圆的又一个重要性质，也是圆中论证同圆或等圆中，弧相等、圆心角相等、弦相等的主要依据，还是研究圆周角以及圆的其他知识的重要基础，是转化思想的具体体现．第四课时 圆周角（第一课时）内容解析 类比圆心角的概念，让学生尝试归纳圆周角的概念.注意：圆心角的顶点在圆心，圆周角的顶点在圆上. 圆周角定理揭示了一条弧所对的圆周角与圆心角之间的数量关系，从而把圆周角与相对应的弧、弦联系起来．圆周角定理及其推论为与圆有关的角的计算及证明角、弧、弦相等数学问题提供了十分便捷的方法和思路．圆周角定理的证明，采用完全归纳法．通过分类讨论，把一般问题转化为特殊情况来证明，渗透了分类讨论和化一般为特殊的化归思想．第四课时 圆周角（第二课时）内容解析 本课时的内容是在学生学习了圆周角和圆心角的关系的基础上，进一步学习圆内接四边形的概念和性质.学生观察圆内接四边形的两组对角与其所对的弧之间的关系，发现每组对角所对的弧都恰好组成整个圆，从而根据圆周角定理，得圆内接四边形的对角互补.这一性质充分揭示了作为直线形的圆内接四边形与圆的内在联系，它是今后证明与圆有关的角互补的重要依据.依据同角的补角相等，得圆内接四边形的任何一个外角都等于它的内对角，这个推论是证明与圆有关的角相等时经常用到．第六课时 点和圆的位置关系内容解析 在研究点和圆的位置关系时，是从其几何特征(交点个数)和代数特性(点到圆心的距离与半径的关系)两个角度刻画的．因此，在探究与圆有关的位置中，点和圆的位置关系是基础．对于经过不在同一直线上的三点作圆的问题，可以从过一点、过两点开始探究，其中体现了转化的思想．同时，在对过一点、过两点、过不在同一直线上的三点作圆的探究，其核心都是要明确确定圆的要素——确定圆心和半径．第七课时 直线和圆的位置关系（第一课时）内容解析本节课是在学生已经学习了点和圆的位置关系后，对直线和圆的位置关系进行探索．为后续学习切线判断定理打好基础．直线与圆的位置关系从两个方面去刻画：一是通过再现海上日出的过程中，探索直线与圆的公共点的个数，将直线与圆的位置分为相交、相切、相离三种情况；二是通过比较直线与圆心的距离与半径，对直线与圆的位置进行分类，二者之间相互对应，相互联系．第八课时 直线和圆的位置关系（第二课时）内容解析 直线和圆相切是直线和圆的位置关系中的一种特殊并且重要的位置关系，圆的切线是研究三角形内切圆、切线长定理和正多边形与圆的关系的基础．切线的判定定理与性质定理揭示了直线和圆的半径的特殊位置关系，即过半径外端并与这条半径垂直．两个定理互为逆命题．切线判定定理的探究过程体现了由一般到特殊的研究方法．第九课时 直线和圆的位置关系（第三课时）内容解析 圆的切线长定理和三角形的内切圆是在学习了切线的性质和判定的基础之上，继续对切线的性质的研究，是在垂径定理之后对圆的对称性又一次的认识．经历探索切线长定理的过程，体会应用内切圆相关知识解决问题，渗透转化思想和方程思想．第十课时 正多边形与圆内容解析 正多边形是生活中的常见图形，而且正多边形和圆关系密切，只要把圆分成若干相等的弧，就可以得到这个圆的圆内接正多边形.本节课还需学生理解正多边形半径和中心、边心距、中心角的概念，进而掌握利用等分圆周的方法画出任意正多边形，体现了正多边形与圆的关系.第十一课时 弧长和扇形公式（第一课时）内容解析 弧长和扇形面积公式是与圆有关的计算中的两个常用公式.弧长公式是在圆的周长公式的基础上，借助部分与整体的练习推导出来的.运用相同的研究方法，利用圆的面积公式推导出扇形的面积公式，进而通过弧长公式表示扇形面积.应用弧长和扇形面积公式可以解决一些简单的实际问题，从而为学习圆锥侧面积公式的推导打好基础.第十二课时 弧长和扇形公式（第二课时）内容解析 圆锥的侧面展开图是平面图形与空间几何体相互转换的教学内容，是培养学生空间想象能力和动手操作能力的重要内容.由于圆锥的侧面展开图是一个扇形，因此，利用弧长和扇形面积公式，可通过计算它的展开图的面积求得圆锥的侧面积，进而可以求出其全面积.结合圆锥侧面积和全面积的学习，有助于培养学生的空间想象能力.课程结束