





初中数学人教版九年级上册24.1.4 圆周角完美版教学课件ppt
展开1 理解圆周角的定义.2 掌握圆周角定理及推论.3 结合圆周角定理的探索与证明的过程,进一步体会分类讨论、化归的思想方法.
【提问】简述圆心角的定义?说出圆心角的判断方法?
圆心角的定义:圆心角的判断方法:
顶点在圆心的角叫做圆心角.
观察顶点是否在圆心.
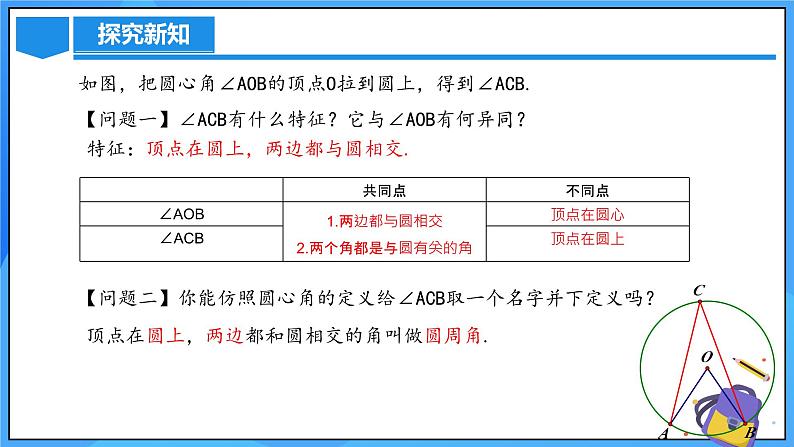
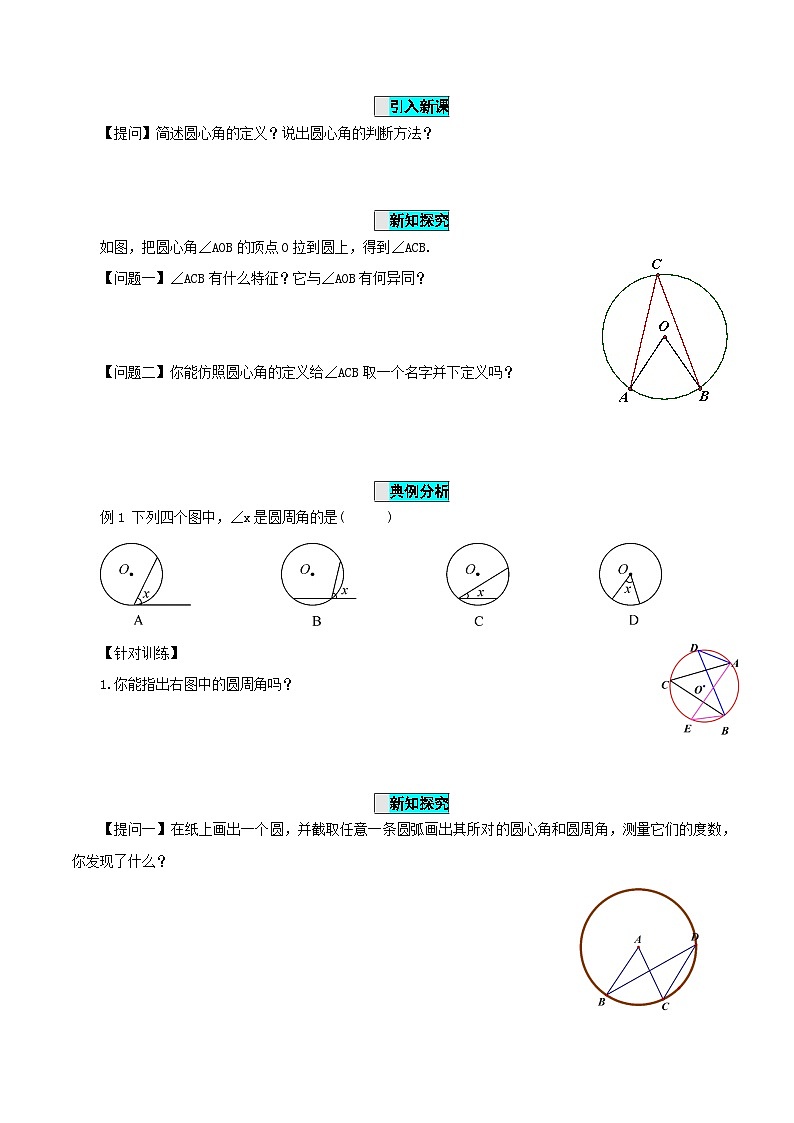
如图,把圆心角∠AOB的顶点O拉到圆上,得到∠ACB.【问题一】∠ACB有什么特征?它与∠AOB有何异同?【问题二】你能仿照圆心角的定义给∠ACB取一个名字并下定义吗?
特征:顶点在圆上,两边都与圆相交.
顶点在圆上,两边都和圆相交的角叫做圆周角.
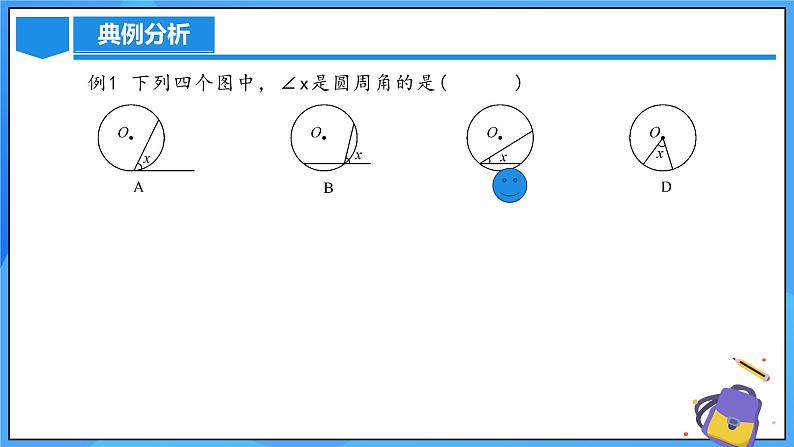
例1 下列四个图中,∠x是圆周角的是( )
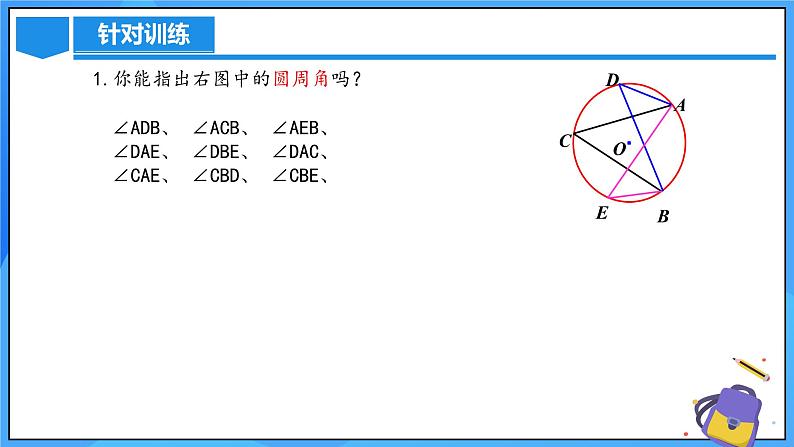
1.你能指出右图中的圆周角吗?
∠ADB、 ∠ACB、 ∠AEB、 ∠DAE、 ∠DBE、 ∠DAC、 ∠CAE、 ∠CBD、 ∠CBE、
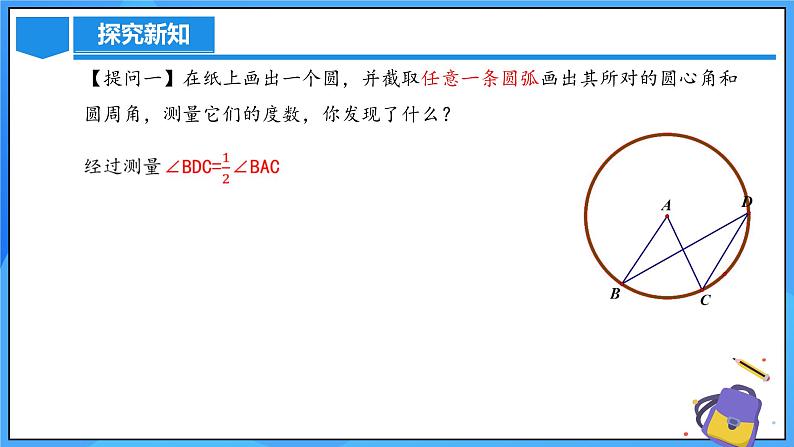
【提问一】在纸上画出一个圆,并截取任意一条圆弧画出其所对的圆心角和圆周角,测量它们的度数,你发现了什么?
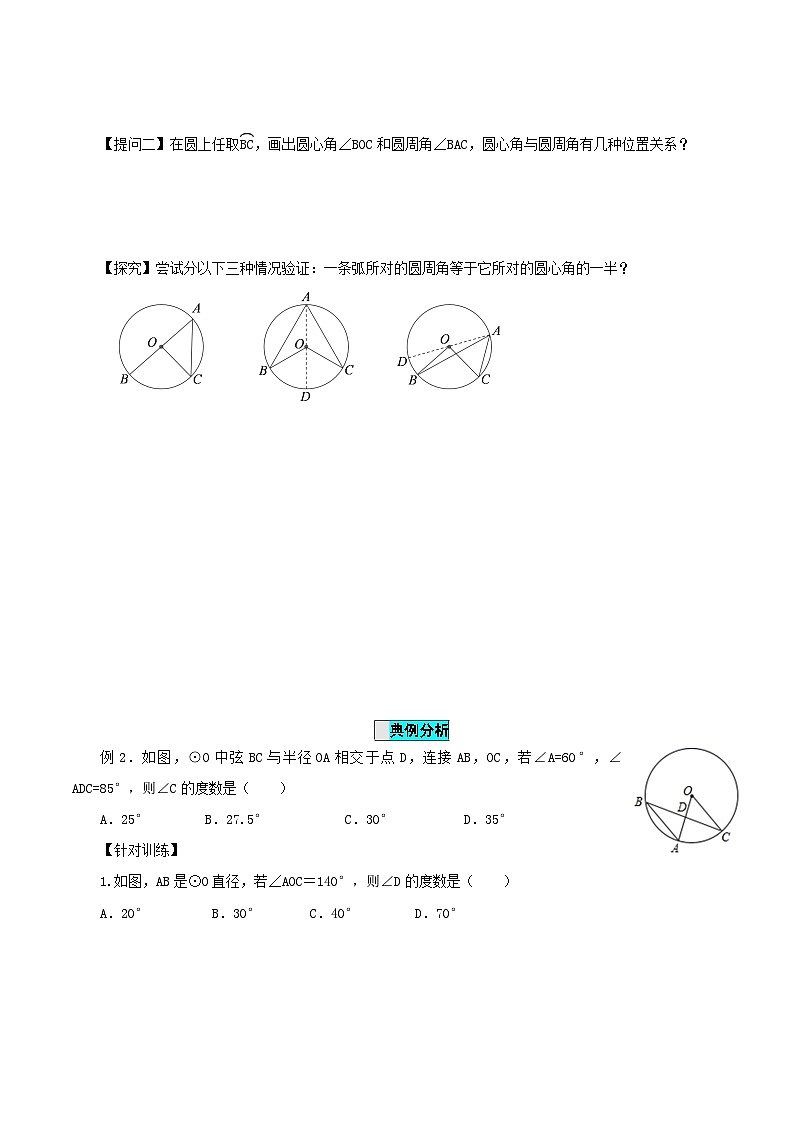
【探究】尝试分以下三种情况验证:一条弧所对的圆周角等于它所对的圆心角的一半?
符号“=>”读作“推出”,“A =>B”表示由A条件推出结论B.
一条弧所对的圆周角等于它所对的圆心角的一半.
例2.如图,⊙O中弦BC与半径OA相交于点D,连接AB,OC,若∠A=60°,∠ADC=85°,则∠C的度数是( )A.25° B.27.5° C.30° D.35°
【解析】∵∠A=60°,∠ADC=85°,∴∠B=25°,∠CDO=95°,∴∠AOC=2∠B=50°,∴∠C=180°-95°-50°=35°故选D.
【详解】由题意得:∠DOB=2∠C,∵∠AOD+∠DOB=180°,∴∠AOD+2∠C=180°,∵∠C+∠AOD=145°,∴∠C=35°,故选B.
3.如图,AB是⊙O的弦,OC⊥AB,交⊙O于点C,连接OA,OB,BC,若∠ABC=20°,则∠AOB的度数是( )A.40° B.50° C.70° D.80°4.如图,已知△ACD和△ABE都内接于同一个圆,则∠ADC+∠AEB+∠BAC=( ) A.90° B.180° C.270° D.360°
【详解】∵∠ABC=20°∴∠AOC=40°∵AB是⊙O的弦,OC⊥AB,∴∠AOC=∠BOC=40°,∴∠AOB=80°,故选:D.
【详解】∵∠ADC,∠AEB,∠BAC所对圆弧正好是一个圆周, ∴∠ADC+∠AEB+∠BAC=180°.故选B.
【详解】解:连接OB、OC,如图,∵∠BOC=2∠BAC=2×30°=60°而OB=OC,∴△OBC为等边三角形,∴OB=BC=6,∴⊙O的直径等于12.
【提问一】回顾同圆和等圆中,圆心角、弧、弦之间的关系吗?
在同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量也相等.
【提问二】想一想圆周角、弧、弦之间的关系吗?
同弧所对的圆周角相等.
等弧所对的圆周角相等.
推论1:同弧或等弧所对的圆周角相等
【提问】你能归纳出圆周角的第一条推论吗?
【探究三】回答下面问题:1.如图1,AB为⊙O的直径,它所对的圆心角是多少?2.如图1,AB为⊙O的直径,它所对的圆周角是多少?3.如图2,AB为⊙O的直径,若改变点C的位置,它所对的圆周角度数会改变吗?4.如图1,在⊙O中若∠C=90°,弦AB经过圆心吗?为什么?
∵∠ACB=90°∴∠AOB=180°∴弦AB过圆心
【提问】你能归纳出圆周角的第二条推论吗?
推论2:直径(或半圆)所对的圆周角是直角; 90°的圆周角所对的弦是直径,所对的弧是半圆.
例3 如图,⊙O的直径AB为10 cm,弦AC为 6 cm,ACB 的平分线交⊙O 于点 D,求 BC,AD,BD 的长.
2.如图,在⊙O中弦AB、CD相交于点P,若∠A=20°,∠APD=70°,则∠B等于( )A.30° B.35° C.40° D.50°3.如图,AB为⊙O直径,CD为⊙O的弦,∠ACD=25°,∠BAD的度数为_______.
【详解】解:∵AB为⊙O直径,∴∠ADB=90°.∵∠B=∠ACD=25°,∴∠BAD=90°﹣∠B=65°.
4. 如图,AB是⊙O的直径,C,D是圆上两点,连接AC,BC,AD,CD.若∠CAB=55°,则∠ADC的度数为( )A.55° B.45° C.35° D.25°5.如图,AB是半圆的直径,C、D是半圆上的两点,∠ADC=106°,则∠CAB等于( )A.10° B.14°C.16° D.26°
6.如图,在⊙A中,已知弦BC=8 DE=6,∠BAC+∠EAD=180°,则⊙A的半径长为( )A.10 B.6 C.5 D.8
8. 有一个圆形模具,现在只有一个直角三角板,请你找出它的圆心?
7.如图,⊙O的直径AB与弦CD垂直,且∠BAC=40°,则∠BOD= .
1.圆周角的概念?2.圆周角定理?3.圆周角定理推论?
P88:练习第2题、第3题、第4题.
初中数学人教版九年级上册第二十五章 概率初步25.3 用频率估计概率获奖教学ppt课件: 这是一份初中数学人教版九年级上册<a href="/sx/tb_c10288_t3/?tag_id=26" target="_blank">第二十五章 概率初步25.3 用频率估计概率获奖教学ppt课件</a>,文件包含253用频率估计概率第一课时pptx、253用频率估计概率第一课时教学设计docx、253用频率估计概率第一课时导学案docx等3份课件配套教学资源,其中PPT共22页, 欢迎下载使用。
初中数学人教版九年级上册25.1.2 概率完美版教学ppt课件: 这是一份初中数学人教版九年级上册<a href="/sx/tb_c24925_t3/?tag_id=26" target="_blank">25.1.2 概率完美版教学ppt课件</a>,文件包含2512概率pptx、2512概率教学设计docx、2512概率导学案docx等3份课件配套教学资源,其中PPT共25页, 欢迎下载使用。
初中第二十四章 圆24.1 圆的有关性质24.1.4 圆周角试讲课教学ppt课件: 这是一份初中<a href="/sx/tb_c88764_t3/?tag_id=26" target="_blank">第二十四章 圆24.1 圆的有关性质24.1.4 圆周角试讲课教学ppt课件</a>,文件包含2414圆周角第二课时pptx、2414圆周角第二课时教学设计docx、2414圆周角第二课时导学案docx等3份课件配套教学资源,其中PPT共21页, 欢迎下载使用。














