











初中数学人教版九年级上册24.2.2 直线和圆的位置关系评优课教学课件ppt
展开1.会判定一条直线是否是圆的切线并会过圆上一点作圆的切线.2.理解并掌握圆的切线的判定定理及性质定理.3.能运用圆的切线的判定定理和性质定理解决问题.
【提问一】判定直线和圆的位置关系的方法有几种?【提问二】直线和圆有哪些位置关系?如何判断直线与圆相切?
判定直线与圆的位置关系的方法有两种:1)根据定义,由直线与圆之间公共点个数来判断;2) 根据数量关系,由圆心到直线的距离d与半径r的关系来判断.
直线与圆的位置关系有三种:相切、相交、相离.
判定直线与圆相切的方法有两种:1)根据定义,当直线与圆之间只有1个公共点时,直线与圆相切;2) 根据数量关系,当圆心到直线的距离d与半径r相等时,直线与圆相切.
【问题一】已知圆O上一点A,怎样根据圆的切线定义过点A作圆O的切线?【问题二】填空(1)直线l与⊙O有______个交点(2)圆心O到直线l的距离d与r的关系是______(3)直线l和⊙O半径r的位置关系是______(4)由此你发现了什么?
1)直线l经过半径OA的外端点A.2) 直线l垂直于半径OA.则直线l与⊙O相切.
这样我们就得到了从位置上来判断直线是圆的切线的方法-切线的判定定理.
∵OA⊥l于点A,OA是半径∴直线l是⊙O的切线.
经过半径的外端并且垂直于这条半径的直线是圆的切线.
【提问】要使直线l是⊙O的切线需要满足哪些条件?
①经过半径的外端;②垂直于这条半径.
两个条件缺一不可,否则就不是圆的切线.
判断一条直线是一个圆的切线有三个方法:
1.定义法:直线和圆只有一个公共点时,我们说这条直线是圆的切线;
2.数量关系法:圆心到这条直线的距离等于半径(即d=r)时,直线与圆相切;
3.判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.
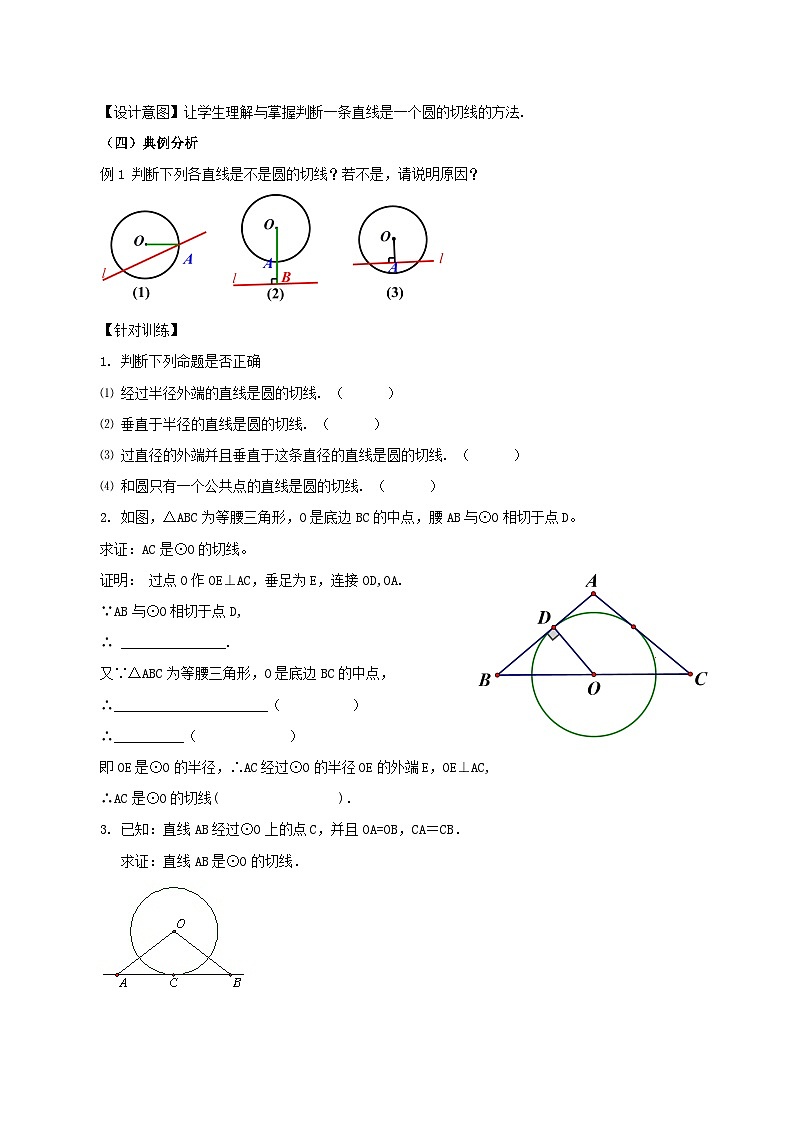
例1 判断下列各直线是不是圆的切线?若不是,请说明原因?
(1)不是,因为没有垂直.
(2)(3)不是,因为没有经过半径的外端点A.
1. 判断下列命题是否正确⑴ 经过半径外端的直线是圆的切线. ( )⑵ 垂直于半径的直线是圆的切线. ( )⑶ 过直径的外端并且垂直于这条直径的直线是圆的切线. ( )⑷ 和圆只有一个公共点的直线是圆的切线. ( )
证明: 过点O作OE⊥AC,垂足为E,连接OD,OA.∵AB与⊙O相切于点D,∴ _______________.又∵△ABC为等腰三角形,O是底边BC的中点,∴______________________( )∴__________( )即OE是⊙O的半径,∴AC经过⊙O的半径OE的外端E,OE⊥AC,∴AC是⊙O的切线( ).
AO是∠BAC的平分线
2. 如图,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于点D. 求证:AC是⊙O的切线.
3. 已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB. 求证:直线AB是⊙O的切线.
证明:连接OC,∵OA=OB,CA=CB,∴OC⊥AB.∵直线AB经过⊙O上的点C,∴OC是半径∴直线AB是⊙O的切线.
【利用切线判定定理解题思路一】已知公共点,连半径,证垂直.
4.已知:OA=OB=5,AB=8,⊙O的直径为6. 求证:直线AB是⊙O的切线.
证明:过点O作OC⊥AB于C,∵OA=OB=5,AB=8, ∴AC=BC=4.在Rt△AOC中,根据勾股定理可得:OC=3∵⊙O的直径为6 ∴OC是⊙O的半径∴直线AB是⊙O的切线.
【利用切线判定定理解题思路二】未知公共点,作垂线,证半径.
5. 如图,AB是⊙O的直径,点C在⊙O上,过点C的直线与AB延长线相交于点P.若∠COB=2∠PCB,求证:PC是⊙O的切线.
证明:连接AC,∵OA=OC,∴∠A=∠ACO.∴∠COB=2∠ACO.又∵∠COB=2∠PCB,∴∠ACO=∠PCB.∵AB是⊙O的直径,∴∠ACO+∠OCB=90°.∴∠PCB+∠OCB=90°,即OC⊥CP.∵OC是⊙O的半径,∴PC是⊙O的切线.
6.1)如图1,AB为直径,要使EF为☉O的切线,还需添加的条件是(只需写出两 种情况):① _________ ;② _____________ .2)如图2,AB是非直径的弦,∠CAE=∠B,求证:EF是☉O的切线.
证明:连接AO并延长交☉O于D,连接CD,则AD为☉O的直径.∴ ∠D+∠DAC=90 °,∵ ∠D与∠B都是弧AC所对的圆周角,∴ ∠D=∠B,又∵ ∠CAE=∠B, ∴ ∠D=∠CAE,∴ ∠DAC+∠EAC=90°,∴EF是☉O的切线.
【问题一】如图,如果直线l是⊙O 的切线,点A为切点,那么OA与l垂直吗?
证明: (1)假设OA与直线l不垂直;过点O作OP⊥直线l于点P(2)因为点到直线的距离垂线段最短,所以OP˂OA,即圆心O到直线l的距离小于⊙O的半径,因此l与⊙O相交,这与已知条件“直线l是⊙O的切线”相矛盾;(3)所以假设不成立,OA⊥直线l.
【问题二】你发现了什么?
∵直线l是⊙O的切线,点A的切点∴OA⊥直线l
圆的切线垂直于过切点的半径.
例2 如图, ⊙O切PB于点B,PB=4,PA=2,则⊙O的半径多少?
解:连接OB,则∠OBP=90°.
设⊙O的半径为r,则OA=OB=r,OP=OA+PA=2+r.
在Rt△OBP中,由勾股定理得
OB2+PB2=PO2,即r2+42=(2+r)2.
有切线时常用辅助线添加方法: 见切线,连切点,得垂直.
1.如图,AB是⊙O的切线,A为切点,连接OA,OB,若∠B=35°,则∠AOB的度数为( )A.65° B.55°C.45° D.35°2. 如图,AB是⊙O的弦,AO的延长线与过点B的⊙O的切线交于点C,如果∠ABO=20°,则∠C的度数是( )A.70° B.50°C.45° D.20°
3.如图,PA、PB是⊙O切线,A、B为切点,点C在⊙O上,且∠ACB=55°,则∠APB等于( )A.55° B.70°C.110° D.125°
【详解】解:连接OA,OB,∵PA,PB是⊙O的切线,∴PA⊥OA,PB⊥OB,∵∠ACB=55°,∴∠AOB=110°,∴∠APB=360°−90°−90°−110°=70°.故选B.
4.如图,AB是⊙O的弦,点C在过点B的切线上,且OC⊥OA,OC交AB于点P,已知∠OAB=22°,则∠OCB=__________.
【详解】连接OB,∵BC是⊙O的切线,∴OB⊥BC,∴∠OBA+∠CBP=90°,∵OC⊥OA,∴∠A+∠APO=90°,∵OA=OB,∠OAB=22°,∴∠OAB=∠OBA=22°,∴∠APO=∠CBP=68°,∵∠APO=∠CPB,∴∠CPB=∠ABP=68°,∴∠OCB=180°-68°-68°=44°,故答案为44°
1.切线的判定方法有几种?分别是什么?2.切线的判定定理与性质定理是什么?它们有怎样的联系?3.简述在应用切线的判定定理和性质定理时,常见辅助线的添加方法?
P101:习题24.2 第4题,第5题,第12题
初中数学人教版九年级上册25.3 用频率估计概率优秀教学课件ppt: 这是一份初中数学人教版九年级上册<a href="/sx/tb_c10288_t3/?tag_id=26" target="_blank">25.3 用频率估计概率优秀教学课件ppt</a>,文件包含253用频率估计概率第二课时pptx、253用频率估计概率第二课时教学设计docx、253用频率估计概率第二课时导学案docx等3份课件配套教学资源,其中PPT共24页, 欢迎下载使用。
初中数学人教版九年级上册25.1.2 概率完美版教学ppt课件: 这是一份初中数学人教版九年级上册<a href="/sx/tb_c24925_t3/?tag_id=26" target="_blank">25.1.2 概率完美版教学ppt课件</a>,文件包含2512概率pptx、2512概率教学设计docx、2512概率导学案docx等3份课件配套教学资源,其中PPT共25页, 欢迎下载使用。
数学人教版24.4 弧长和扇形面积公开课教学课件ppt: 这是一份数学人教版<a href="/sx/tb_c10276_t3/?tag_id=26" target="_blank">24.4 弧长和扇形面积公开课教学课件ppt</a>,文件包含244弧长和扇形公式第二课时pptx、244弧长和扇形公式第二课时教学设计docx、244弧长和扇形公式第二课时导学案docx等3份课件配套教学资源,其中PPT共26页, 欢迎下载使用。














